
- •Министерство образования и науки рф
- •1. Графический метод решения задачи линейной оптимизации
- •Таким образом, необходимо выпустить 6 шт. Изделий а1, 4 шт. Изделий а2, чтобы получить прибыль 24 ден.Ед.
- •2. Симплексный метод решения задачи линейного программирования. Двойственная задача
- •3. Транспортная задача
- •Вариант № 1
- •1. Найти решение задачи лп, используя графический метод.
- •2. Составить математическую модель задачи.
- •Вариант № 3
- •1. Найти решение задачи лп, используя графический метод.
- •2. Составить математическую модель задачи.
- •4. Решить транспортную задачу.
- •Вопросы к экзамену по дисциплине «Методы оптимальных решений» для студентов 1 курса (заочная и сокращенная формы обучения)
- •Литература
1. Графический метод решения задачи линейной оптимизации
Графический метод решения ЗЛП состоит из следующих этапов.
Строится область допустимых решений (ОДР) ЗЛП.
Строится вектор-градиент целевой функции в какой-нибудь точке Х0, принадлежащей ОДР –
 .
.Линия уровня C1x1+C2x2 = а (а – постоянная величина) - прямая, перпендикулярная вектору–градиенту
 – передвигается в направлении этого
вектора в случае максимизацииf(x1,x2)до тех пор, пока не покинет пределов
ОДР. Предельная точка (или точки) области
при этом движении и является точкой
максимумаf(x1,x2).
– передвигается в направлении этого
вектора в случае максимизацииf(x1,x2)до тех пор, пока не покинет пределов
ОДР. Предельная точка (или точки) области
при этом движении и является точкой
максимумаf(x1,x2).Для нахождения ее координат достаточно решить систему из двух уравнений прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1,x2),найденное в полученной точке, является максимальным.
При минимизации f(x1,x2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимумf(x1,x2)не существует.
Если линия уровня параллельна какой-либо прямой из ограничений задачи, то оптимальное значение целевой функции будет достигаться в любой точке этой прямой.
Пример. Для изготовления двух видов продукции А1 и А2 используют три вида ресурсов S1, S2, S3, запасы которых составляют и усл. ед. соответственно. Расход ресурсов на ед. продукции приведен в таблице:
|
Виды ресурсов |
Запасы ресурсов |
Расходы ресурсов на 1 изд. | |
|
А1 |
А2 | ||
|
S1 |
|
|
|
|
S2 |
|
|
|
|
S3 |
|
|
|
|
|
Прибыль |
руб. |
руб. |
Необходимо составить такой план производства продукции, который обеспечит наибольшую прибыль от ее реализации.
Решение. Составим экономико-математическую модель задачи.
Пусть надо выпустить изделий A1 - x1 шт., а изделий А2 - x2 шт. Тогда прибыль от реализации составит 2x1 + 3x2 и она должна быть максимальной. Получим целевую функцию: F=2x1 + 3x2→ max.
На одно изделие А1 затрачивается 1 усл. ед. ресурса S1, тогда на x1 шт. затратится x1 усл. ед. На одно изделие А2 затрачивается 3 усл. ед. ресурса S1, тогда на x2 шт. затратится 3x2 усл. ед. На оба изделия затратится x1+ 3x2 усл. ед. ресурса S1. Так как всего в наличие 18 усл. ед., то получим первое ограничение: xx18. Аналогично получим остальные ограничения.
Запишем модель: найти максимальное значение функции F=2x1 + 3x2 при условиях
|
|
|
|
xx |
|
|
x |
|
|
x |
x |
Построим область допустимых значений:
1) первое ограничение по ресурсу S1 xx; прямая xx= проходит через точки ; неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка < принадлежит полуплоскости);
2) второе ограничение по ресурсу S2 2xx: прямая 2xx= проходит через точки ; неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка < принадлежит полуплоскости);
3) неравенству x соответствует полуплоскость, содержащая прямую x= и лежащая ниже неё.
4) x1правее ОX;
5) x2выше ОX1.
Рис. 1.
Вектор-градиент
имеет координаты

Построим линии уровня xx = а. При а = получим прямую xx =, проходящую через точки. Так как задача на максимум, то передвигаем линию уровня в направлении градиента. Предельной точкой (последней из области допустимых решений, с которой соприкасается линия уровня) является точка С. Значит, в ней достигается максимум функции F.
Найдём её координаты. Для этого решим систему:
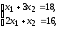


 xx
xx