Катушка индуктивности

И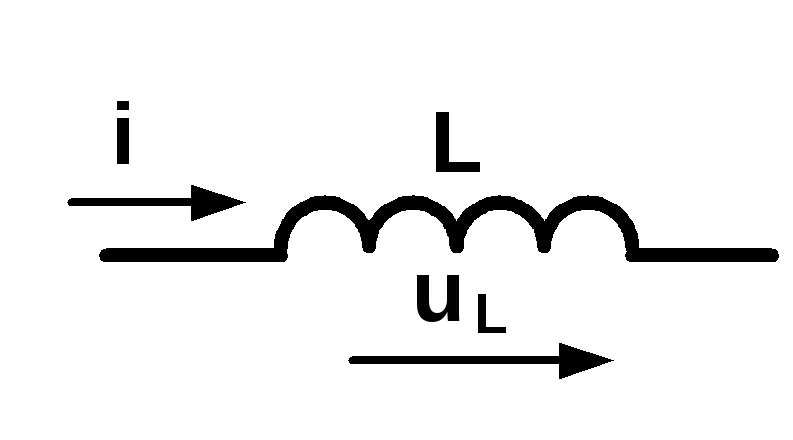деальная катушка индуктивности – это элемент электрической цепи, запасающий электрическую энергию в магнитном поле, которую может полностью возвратить в последующем. Поэтому идеальная катушка индуктивности активную энергию не потребляет, и её активная мощность равна нулю

(P = 0 — для идеальной катушки).

М

Рис 5.4.6. Обозначение идеальной катушки

индуктивности

атематическая модель идеальной катушки индуктивности отражает то, что приложенное к ней напряжениеu_L уравновешивается ЭДС самоиндукции e .

u_L = – e = L ,

где L – индуктивность катушки, измеряемая в Генри (Гн).

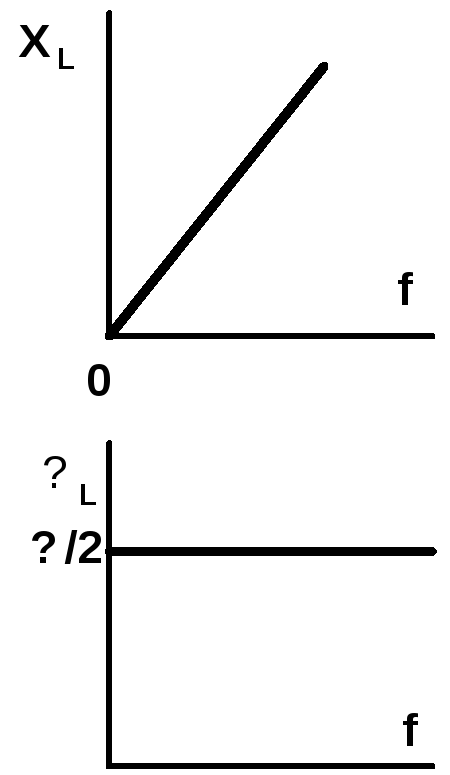На переменном токе катушка обладает индуктивным сопротивлением

X_L = ωL = 2πfL (Ом),

которое может быть определено через действующее значение напряжения на катушке и действующее значение протекающего по ней тока по формуле:

X_L = (Ом).

X_L= const – для линейных катушек индуктивности.

Рис 5.4.7. Частотные характеристики

идеальной катушки индуктивности

В соответствии с формулой сопротивления идеальной катушки индуктивности видно, что оно пропорционально частоте f.

В то же время сдвиг по фазе между напряжением и током идеальной катушки индуктивности равен π/2.

Частотные характеристики идеальной катушки индуктивности X_L(f) и φ_L(f) представлены на рис. 5.4.7.

В комплексной форме сопротивление идеальной катушки индуктивности чисто мнимое.

Z_L = jX_L = jωL = j2πfL,

и

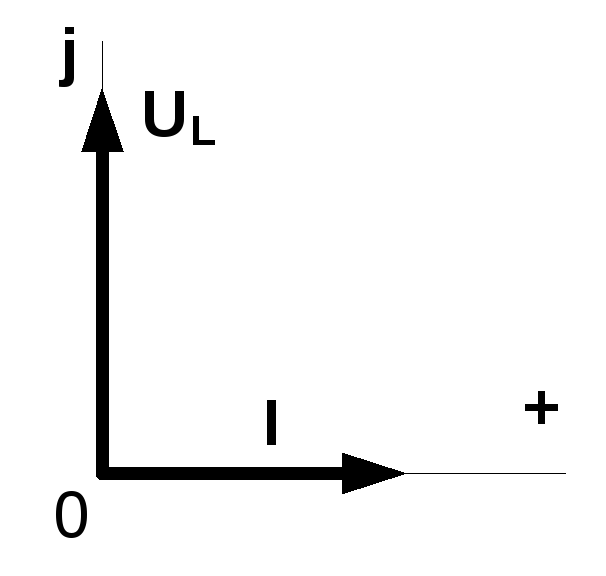
Рис. 5.4.8 Векторная диаграмма идеальной катушки индуктивности

закон Ома для идеальной катушки индуктивности в комплексной форме имеет вид

Ủ_L = Z_L Ỉ= jX_LỈ = jωLỈ = j2πfLỈ .

В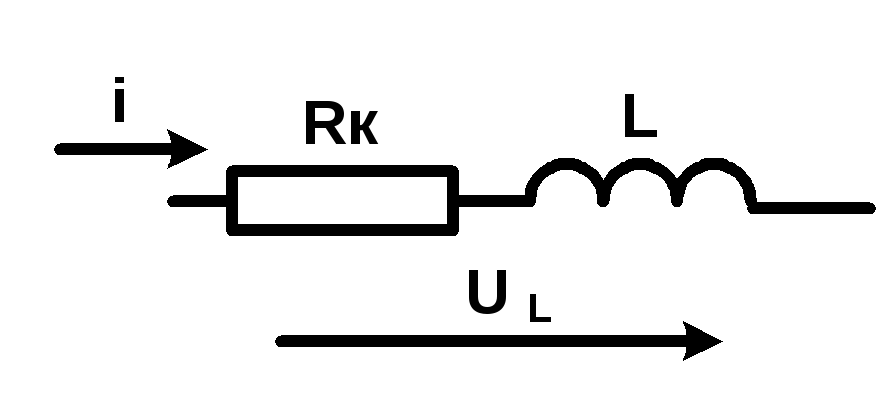екторная диаграмма, соответствующая этой формуле, представлена на рис. 5.4.8.

Из неё видно, что напряжение на идеальной катушке индуктивности опережает ток на π/2.

О

Рис. 5.4.9. Схема замещения реальной катушки индуктивности

днако реальная катушка индуктивности намотана проводом, обладающим активным сопротивлениемR_k. Поэтому реальная катушка индуктивности потребляет активную энергию, и её активная мощность определяется формулой.

P_K = R_k I² Вт.

В то же время максимальный запас энергии в магнитном поле катушки индуктивности характеризуется её реактивной мощностью Q, измеряемой в ВАр.

ВАр.

Конденсатор

Конденсатор – это элемент электрической цепи, запасающий электрическую энергию в электрическом поле, которую может полностью возвратить в последующем. Поэтому конденсатор активную энергию не потребляет, и его активная мощность равна нулю (P = 0).

М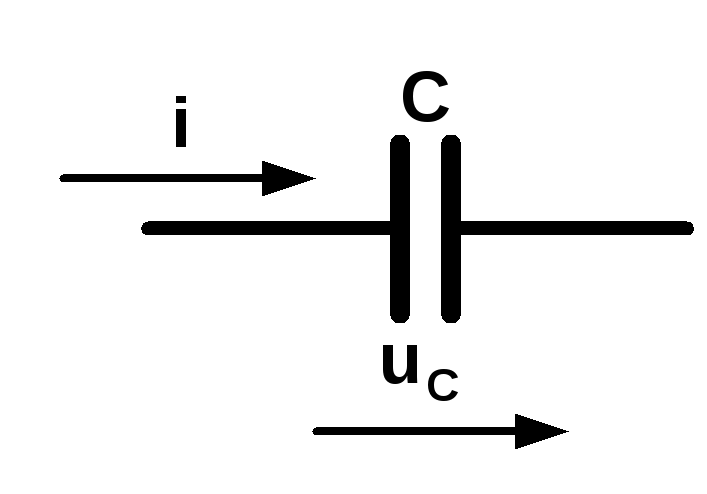атематическая модель конденсатора

i = ,

г

Рис. 5.4.10. Обозначение конденсатора

деС – ёмкость конденсатора, измеряемая в Фарадах (Ф) или в микрофарадах(1 мкФ = 10 ^-6 Ф).

На переменном токе конденсатор обладает ёмкостным сопротивлением.

X_С = (Ом),

которое может быть определено через действующее напряжение на конденсаторе и протекающий через его действующий ток по формуле:

X_C = (Ом).

X_C = const – для линейных катушек индуктивности.

В

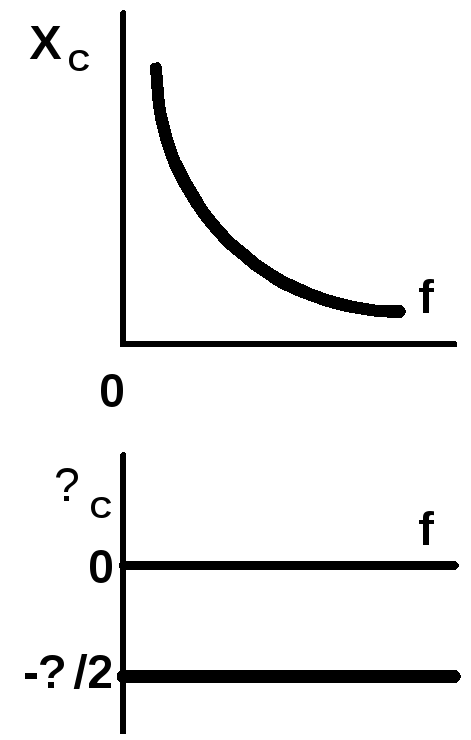
Рис. 5.4.11. Частотные

характеристики конден

сатора

соответствии с формулойсопротивления конденсатора видно, что оно обратнопропорционально частоте f.

В то же время сдвиг по фазе между напряжением и током конденсатора равен –π/2.

Частотные характеристики конденсатора X_C(f) и φ_C(f) представлены на рис. 5.4.11.

В комплексной форме сопротивление конденсатора чисто мнимое.

Z_С = = – j=–jX_C (Ом).

Закон Ома для конденсатора в комплексной форме имеет вид

Ủ_C = Z_C Ỉ= – jỈ .

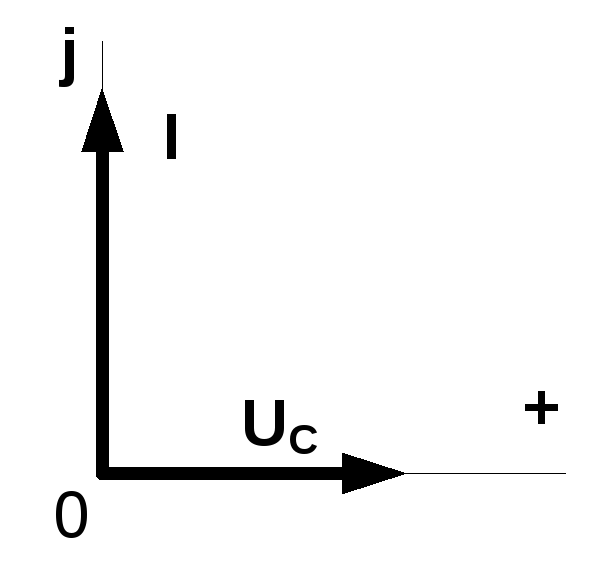
Векторная диаграмма, соответствующая этой формуле, представлена на рис. 5.4.12.

Из неё видно, что ток конденсатора опережает напряжение на π/2.

Рис. 5.4.12. Векторная

диаграмма конденсатора