2. Потенциал. Связь напряжённости электрического поля с потенциалом Основные формулы

Потенциал электростатического поля

,

где W_n– потенциальная энергия точечного положительного зарядаQ₀, помещённого в данную точку поля.

Разность потенциалов в двух точках поля

,

где А– работа по перемещению зарядаQиз точки с потенциалом в точку с потенциалом.

Работа А

.

Потенциал поля точечного заряда Qна расстоянииrот заряда

,

где м/Ф;ε– диэлектрическая проницаемость среды.

Принцип суперпозиции для потенциалов электростатических полей

,

где – расстояние от зарядаQ_iдо точки, в которой вычисляется потенциал.

Потенциальная энергия взаимодействия двух точечных зарядов Q₁иQ₂

.

Энергия взаимодействия системы точечных зарядов Q₁,Q₂, …,Q_n

,

где – потенциал поля, создаваемого всемиn-1 зарядами (за исключениемi-го) в точке, в которой расположен зарядQ_i.

Связь потенциала φ с напряжённостью электростатического поля

,

где grad– операция «градиент», действие которой на функцию φ(x,y,z) в декартовых координатах задаётся уравнением

,

где ,,– орты координатных осейx,y,z.

В случае центрально симметричного электрического поля, а также поля цилиндрической симметрии

,

где r– расстояние отцентра симметрии, или соответственно от оси цилиндрической симметрии до точки наблюдения.

В случае однородного поля

,

где d– проекция отрезка, соединяющего точки с потенциалами и , на направление силовой линии поля.

Примеры решения задач

Пример 1

Три точечных заряда Q₁= 1 мкКл,Q₂= -2 мкКл,Q₃= 4 мкКл находятся на бесконечно больших расстояниях друг от друга. Найти: а) работу, которую нужно совершить, чтобы расположить заряды в вершинах правильного треугольника со сторонойа= 0,1 м; б) потенциальную энергию зарядаQ₁после перемешения зарядов.

Дано:

а) А -? б) Wn1 -?

Решение

После перемещения зарядов:

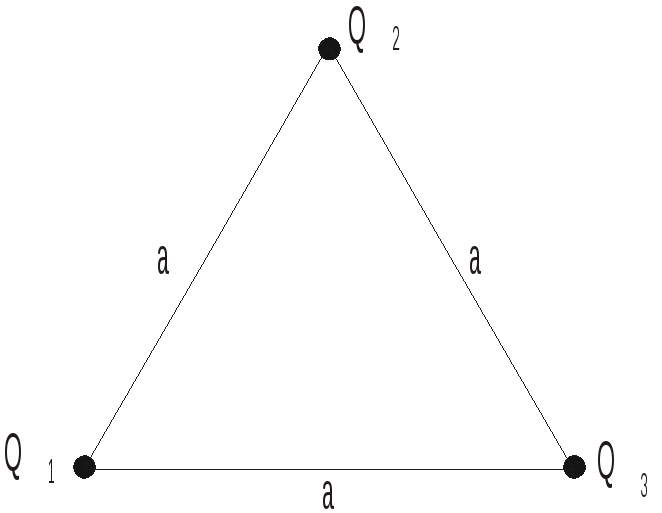
а) Работа Аравна изменению потенциальной энергии:А= |W_nкон-W_nнач|.

W_nнач= 0;W_nкон=W₁₂+W₂₃+W_13;

.

Дж.

б) Дж.

Ответ: а) А= 0,54 Дж; б)W_n1=0,45 Дж.

Пример 2

Бесконечная тонкая равномерно заряженная нить имеет линейную плотность заряда Кл/м. Какую скорость приобретет электрон, переместившись из точки на расстоянииr₁= 0,1 м в точку на расстоянииr₂= 0,2 м от нити? Отношение модуля заряда электрона к его массе Кл/кг. Начальная скорость электрона равна нулю.

Дано: Кл/м r1 = 0,1 м r2= 0,2 м Кл/кг υ0= 0

υ = ?

Решение

По теореме о кинетической энергии работа , т.к..

С другой стороны, работа А

тогда.

Из уравнения, связываюшего потенциал и напряженность электрического поля в случае цилиндрической симметрии ,следует:.

Напряженность Еполя нити . Тогда скорость.

м/с.

Ответ: м/с.

Пример 3

Диэлектрический шар радиусом0,2 м сравномерно заряжен по объему с объемной плотностью заряда мкКл/м³. Найти разность потенциалов между точками, расположенными на расстоянияхr₁= 0,1 м и r₂= 0,4 м от центра шара.

Дано: R = 0,2м мкКл/м3 r1= 0,1 м r2= 0,4 м

Решение

Связь Еи для центрально симметричного поля

.

Напряженность электрического поля шара в зависимости от расстояния rдо центра шара

–электрический заряд шара.

В.

Ответ: В.

Пример 4

Две тонкие концентрические металлические сферы радиусами R₁= 0,2 м иR₂= 0,4 м имеют зарядыQ₁= 200 нКл иQ₂= -160 нКл. Найти потенциалы электрического поля в точках А, В и С, расположенных на расстоянияхr_A= 0,1 м;r_B= 0,3 м; иr_C= 0,5 м от общего центра сфер.

Дано: R1 = 0,2 м R2 = 0,4 м Q1 = Кл Q2 = Кл rA= 0,1 м rB= 0,3 м rC= 0,5 м

- ?

Решение

Потенциал внутри первой сферы одинаков во всех точках внутри этой сферы и по принципу суперпозиции для потенциалов

Потенциал,

где совпадает с потенциалом поля точечного заряда, равногоQ₁и расположенного в т. О; – потенциал поля, создаваемого сферой «2» во всех точках между сферами.

В.

Потенциал в точке вне обеих сфер совпадает с потенциалом поля точечных зарядов, равныхQ₁иQ₂, помещенных в т.O:, где, .

Тогда

В.

Ответ:В,В,В.

Пример 5

Тонкое кольцо радиуса R= 0,3 м равномерно заряжено с линейной плотностью зарядамкКл/м. Найти работу по перемещению точечного зарядаQ= 20 нКл из центра кольца вдоль оси кольца на расстояниеh= 0,4 м плоскости кольца.

Дано: R= 0,3 м Кл/м Q= h = 0,4м

A- ?

Решение

Выберем ось координат, совпадающую с осью кольца с началом в центре кольца. Определим зависимость потенциала кольца от расстояния «Y» до его центра. По принципу суперпозиции для потенциалов

,

где ; м/Ф;.

Для всех зарядов dQкольца расстояниеrдо точкиА, в которой вычисляем потенциал, есть величина постоянная, следовательно,

,,

Работа Апо перемещению зарядаQиз центра кольца в точку, расположенную на оси кольца на расстоянииhот его плоскости,

Дж.

Ответ: Дж.

Пример 6

Два электрона, находясь первоначально на бесконечном расстоянии друг от друга, движутся навстречу друг другу со скоростями, равными по величине 10 м/с. На какое минимальное расстояние сблизятся электроны?

Дано: υ0 = 10 Мм/с = 107м/с

rm - ?

Решение

По закону сохранения энергии

W₁=W₂, или,

где кг,Кл – масса и заряд электрона.

Отсюда м.

Ответ:r_m = м.

Пример 7

В условиях предыдущей задачи один из электронов первоначально покоился. Найти минимальное расстояние между электронами.

Дано: м/с

rm -?

Решение

а) По закону сохранения импульса или, гдескорость каждого электрона в момент наибольшего сближения. Имеем.

б) По закону сохранения энергии W₁=W₂,или,или .

Отсюда м.

Ответ: м.

Замечание:равенство скоростей электронов в момент их наибольшего сближения, когда потенциальная энергия их взаимодействия максимальна, означает, что их кинетическая энергия минимальна, что достигается тогда, когда скорость относительного движения минимальна, т.е. равна нулю.