3. Закон био-савара-лапласа. Теорема о циркуляции магнитного поля.

Закон Био-Савара-Лапласа

,

где m₀ = 4p×10^-7 Гн/м – магнитная постоянная, m - магнитная проницаемость среды, I – сила тока в проводнике, - элемент тока, протекающего в участке , - радиус-вектор, направленный от элемента тока к точке, в которой определяется магнитная индукция .

В скалярной форме:

dB = mm₀I×dl×sina/(4pr²),

где a - угол между векторами и .

Магнитная индукция в центре кругового тока:

B = mm₀I/(2R),

где R – радиус кругового тока силой I.

Магнитная индукция поля, создаваемого отрезком провода с током, являющегося частью бесконечного прямолинейного проводника:

B = mm₀I(cosa₁ - cosa₂)/(4ph),

г де - a₁ и a₂ – углы, под которыми виден отрезок с током из точки наблюдения А, h – расстояние от отрезка с током (или его продолжение) до точки наблюдения А.

Теорема о циркуляции вектора магнитной индукции:

,

где SI_охв – алгебраическая сумма токов, охватываемых контуром L.

Магнитная индукция поля, создаваемого точечным движущимся зарядом (2-я формула закона Био-Савара-Лапласа):

,

где - скорость заряда q, - радиус-вектор, направленный от заряда к точке наблюдения.

В скалярной форме:

В= mm₀qu×sina/(4pr²),

a - угол между вектором скорости и радиус-вектором.

Принцип суперпозиции магнитных полей:

,

где - индукция магнитного поля в некоторой точке, - индукция магнитного поля i-го участка проводника в этой точке.

Примеры решения задач

Задача 1. Вычислить магнитную индукцию в точке 0 для бесконечного проводника с током, изображенного на рисунке. Принять R = 0,1 м, I = 10 А, j = 30⁰.

Решение.

По принципу суперпозиции для магнитных полей магнитная индукция в точке 0:

, где - магнитные индукции в точке 0 от 1-го, 2-го и 3-го участков проводника соответственно.

Для 1-го участка используем формулу индукции магнитного поля отрезка проводника:

B₁ = m₀I(cosa₁ - cosa₂)/(4ph), где h = R, a₁ = 0⁰, a₂ = 90⁰. Следовательно, B₁ = m₀I/(4pR).

Магнитная индукция кольцевого тока в центре кольца B_к = m₀I/(2R). Участок 2 составляет 2/3 окружности радиуса R, тогда B₂ = m₀I/(3R).

Для участка 3 рассмотрим магнитную индукцию в точке 0, создаваемую элементом участка по закону Био-Савара=Лапласа . Поскольку çç , то , т.е. и В₃ = 0. Учитывая, что в точке 0 по правилу буравчика вектор направлен "к нам", а вектор "от нас", получим:

В = В₂ - В₁ = m₀I/(3R) - m₀I/(4pR) = m₀I(1/3 -1/4p)/R.

В = 4×3,14×10(0,333 - 0,08)/0,1=3,2×10^-5 Тл.

Ответ: В = 3,2×10^-5 Тл.

Задача 2. Два бесконечных проводника с токами I₁ = 30 F, I₂ = 40 А представляют собой взаимноперпендикулярные скрещивающиеся прямые, расстояние между которыми равно h = 0,2 м. Найти индукцию магнитного поля в точке, расположенной посередине между проводниками.

Решение.

Проведем через проводники с токами две параллельные плоскости. Отрезок MN перпендикулярен обеим плоскостям. Его концы лежат на проводниках. Отрезок представляет собой минимальное расстояние h между проводниками. Точка А расположена посередине отрезка MN. По принципу суперпозиции магнитных полей . Векторы построены по правилу буравчика для 1-го и 2-го проводника соответственно, причем . По теореме Пифагора . По формуле индукции магнитного поля бесконечного прямолинейного проводника с током: B₁ = m₀I₁/(2p 0,5×h), B₂ = m₀I₂/(2p×0,5×h). Тогда

.

Тл.

Ответ: В_А = 10^-4 Тл.

Задача 3. Протон движется в вакууме по прямой с постоянной скоростью 10⁶ м/с по направлению к некоторой точке С. Точка А расположена на расстоянии h = 6 м от точки С так, что отрезок АС перпендикулярен траектории протона. Найти индукцию магнитного поля, создаваемого протоном в точке А в тот момент, когда расстояние от протона до точки С равно l = 8 м.

Решение.

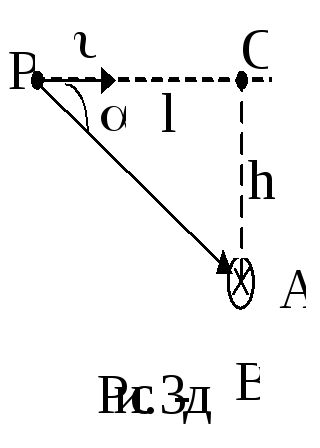По закону Био-Савара-Лапласа магнитная индукция, создаваемая протоном в точке А,

,

– радиус-вектор проведенный от протона в точку А, q = 1,6×10^-19 Кл – заряд протона.

В скалярном виде B = m₀qu×sina/(4pr²),

где a - угол между вектором скорости и радиус-вектором.

По правилу буравчика вектор магнитной индукции направлен перпендикулярно плоскости, в которой лежат векторы скорости и радиус-вектор, "от нас".

По теореме Пифагора r² = l² + h², по определению синуса прямоугольного треугольника sina = h/r.

Тогда B = m₀qu×h/(4p(l² + h²)^3/2).

В = 4×3,14×10^-7×1,6×10^-19×10⁶×6/(4×3,14(8² + 6²)^3/2) = 9,6×10^-23 Тл.

Ответ: В = 9,6×10^-23 Тл.

Задача 4. По бесконечному прямолинейному цилиндрическому проводнику радиуса R = 0,1 м протекает постоянный электрический ток плотностью j = 800 А/м² по сечению проводника. Найти напряженность магнитного поля в точках, расположенных на расстояниях r₁ = 0,05 м, r₂ = 0,2 м.

Решение.

Проведем круговой контур L₁ радиуса r₁ с центром на оси проводника. По теореме о циркуляции вектора напряженности магнитного поля

,

где SI_охв1 – алгебраическая сумма токов, охватываемых контуром L_1.

В любой точке контура || и = const;

SI_охв1 = J×S₁ = J×p×r²₁, где S₁ – площадь круга радиуса r₁.

Получим Н_l = Н = const для точек контура L₁, тогда , или Н₁×2pr₁ = jpr₁². Следовательно, Н₁ = jr₁/2 = 800×0,05/2 = 20 А/м.

Выберем контур L₂ радиуса r₂ с центром на оси проводника. По теореме о циркуляции вектора напряженности магнитного поля

, где åI_охв2 = jS = jpR², где S – площадь поперечного сечения проводника, Н₂ = const для всех точек контураL₂.

Получим: Н₂×2pr₂ = jpR², отсюда Н₂ = jR/(2r₂),

Н₂ = 800×0,1²/(2×0,4) = 10 А/м.

Ответ: Н₁ = 20 А/м, Н₂ = 10 А/м.

Задача 5. По плоскости протекает электрический ток с линейной плотностью j = 80 А/м (ток, приходящийся на единицу длины в направлении перпендикулярном току). Найти индукцию магнитного поля тока плоскости.

Решение.

Выберем контур L в виде прямоугольника с основанием а и высотой b, плоскость которого перпендикулярна плоскости с током и который делится плоскостью тока пополам параллельно основаниям прямоугольника.

Мысленно разделим плоскость с током на узкие параллельные полосы вдоль направления тока. Линии магнитной индукции для тока, протекающего по каждой полосе, представляют собой окружности с центрами на полосах и с направлением по ходу часовой стрелки. Если по принципу суперпозиции сложить векторы магнитной индукции от каждой полосы, то над плоскостью получим вектор , направленный горизонтально влево, а под плоскостью - вектор , направленный горизонтально вправо. По теореме о циркуляции вектора магнитной индукции , где åI_охв – суммарный ток, охватываемый контуром L. Для верхнего и нижнего оснований прямоугольника , а для боковых сторон и В_L = 0. åI_охв = j×а. Тогда 2Ва = m₀/jа. Следовательно, В = m₀×j/2.

В = 4×3,14×10^-7×80/2 = 5×10^-5 Тл.

Ответ: В = 5×10^-5 Тл.