2. Взаимодействие магнитного поля с электрическим током

Сила Ампера – это сила, с которой магнитное поле действует на элемент тока :

dF = IBdlsin,

где I – сила тока в проводнике, dl – длина проводника, В – индукция магнитного поля.

Направление силы Ампера определяется правилом левой руки: ладонь руки располагается так, чтобы четыре вытянутых пальца указывали направление элемента тока, а вектор магнитной индукции входил в ладонь, тогда отогнутый на 90⁰ большой палец укажет направление силы Ампера.

Момент силы, действующий на контур с током в магнитном поле

,

г де - магнитный момент контура (S и I- площадь контура и сила тока в нем, - единичный вектор нормали к плоскости контура).

В векторном виде:

М = p_mВsin, где  - угол между векторами и .

Работа силы Ампера по перемещению контура с током в магнитном поле:

А = I(Ф₂ - Ф₁), где Ф₂ и Ф₁ – магнитные потоки через контур в начальном и конечном состоянии.

Магнитный поток через плоскость контура: ,

где , dS – площадь контура,  - угол между вектором нормали к контуру и вектором магнитной индукции.

В задачах этого раздела сделаны следующие допущения:

вспомогательные проводники расположены вне магнитного поля или направлены так, что сила Ампера на них не действует;

при движении проводников вспомогательные провода не оказывают сопротивления этому движению;

при движении проводников в магнитном поле явления, связанные с электромагнитной индукцией, считаются несущественными.

Примеры решения задач

Задача 1. По проводнику в форме полуокружности радиусом R = 0,2 м протекает ток I = 10 А. Перпендикулярно плоскости проводника создано магнитное поле с индукцией В = 0,4 Тл. На сколько увеличится сила, действующая на проводник, если его распрямить в плоскости полуокружности?

Решение.

Найдем силу F₁, действующую на проводник в форме полуокружности. Мысленно разобьем полуокружность на малые элементарные дуги dl. Равнодействующая всех сил, действующих на элементы : .

Разложим вектор на две составляющие: . Тогда

.

Поскольку вклады в F_х элементов dl и dl, симметричных относительно оси оу, взаимно компенсируются, следовательно, . Так как , тогда , где dF_y = dFcos. По закону Ампера dF = IBdlsin, где  - угол между вектором и направлением тока равен 90⁰, dl = Rd.

Окончательно получаем .

Сила Ампера F₂, действующая на прямой проводник

F₂ = IBL,

где L = R – длина проводника. Следовательно F₂ = IBR.

Разность сил равна: F₂ – F₁ = ( - 2)IBR.

F₂ – F₁ = (3,14 – 2)100,40,2 = 0,9 Н.

Ответ: F₂ – F₁ = 0,9 Н.

Задача 2. Прямолинейный проводник длиной L = 0,5 м массой m = 20 г висит горизонтально на двух параллельных нитях равной длины. Магнитное поле с индукцией В = 0,4 Тл создано в вертикальном направлении. На какой угол отклонятся нити с проводником от вертикали, если по проводнику пропустить ток I = 1 А?

Решение.

Условие равновесия проводника:

,

где  натяжение нити, F_A = IBLsin90⁰ – сила Ампера.

В проекциях на оси координат:

ох: F_A – 2Tsin = 0,

oy: 2Tcos - mg =0.

или

Решая систему данных уравнений, получаем: , следовательно,  = 45⁰.

Ответ:  = 45⁰.

Задача 3. Квадратная рамка со стороной а = 0,1 см, по которой протекает ток силой I =20 А, помещена в магнитное поле с индукцией В =0,5 Тл так, что угол между нормалью к рамке и вектором индукции магнитного поля равен  = 30⁰. Найти вращающий момент М, действующий на рамку со стороны магнитного поля.

Решение.

Магнитный момент М, действующий на рамку с током равен

М = р_mВsin,

где р_m = IS – модуль магнитного момента рамки, S = а² – площадь рамки.

Следовательно, М = Iа²Bsin

М = 200,1²0,50,87 = 0,087 Нм.

Ответ: М = 0,087 Нм.

Задача 4. Тонкий равномерно заряженный стержень вращается с постоянной угловой скоростью вокруг оси, перпендикулярной стержню и проходящей через один из его концов. Линейная плотность заряда стержня  = 2 мкКл/м, линейная плотность стержня  = 0,4 кг/м. Найти отношение магнитного момента стержня к его моменту импульса .

Решение.

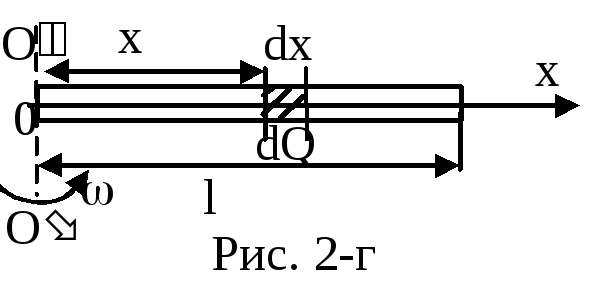Пусть l – длина стержня,  - его угловая скорость, ось ох проходит вдоль стержня перпендикулярно оси вращения ОО. Мысленно разобьем стержень на бесконечно малые элементы dx. Элемент dх имеет элементарный заряд dQ = dх. Сила эквивалентного тока при вращении заряда dQ равна

,

где - период вращения.

Модуль магнитного момента эквивалентного тока равен

dp_m = SdI,

где S = x² – площадь круга.

С учетом вышесказанного .

Проинтегрируем dр_m по х в пределах от 0 до l:

.

Модуль момента импульса стержня:

L = J,

где J – момент инерции стержня относительно оси, проходящей через конец стержня. По теореме Штейнера ,

где m = l – масса стержня. Следовательно, .

Отношение магнитного момента к моменту импульса равно

Кл/кг;

Кл/кг.

Ответ: Кл/кг.

Задача 5. Контур, имеющий форму окружности радиуса R = 0,1 м, помещен в однородное магнитное поле с индукцией В = 0,8 Тл так, что плоскость контура параллельна вектору магнитной индукции. Найти работу сил магнитного поля А по повороту контура на 90⁰ вокруг диаметра окружности, перпендикулярного вектору магнитной индукции. Сила тока в контуре I = 10 А.

Решение.

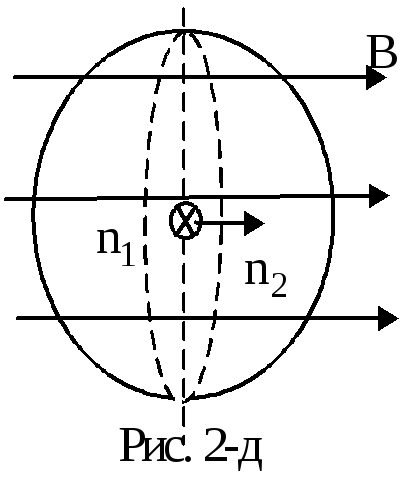Работа по повороту контура:

А = I(Ф₂ – Ф₁),

где Ф₁ = BScos90⁰ – начальный магнитный поток вектора магнитной индукции через контур, Ф₂ = BScos0⁰ – конечный магнитный поток, S = R² – площадь контура.

Следовательно, А = IBR².

А = 3,14100,80,1² = 0,25 Дж.

Ответ: А = 0,25 Дж.