Методические рекомендации Решение обыкновенных дифференциальных уравнений.

Задача Коши.

Пусть дано обыкновенное дифференциальное уравнение первого порядка, разрешенное относительно производной функции :

при начальном условии .

Численно решить уравнение – это значит в некоторых точках (t₁, t₂, … , t_N) найти приближения x₁, x₂, . . . , x_N для значений точного решения x(t₁), x(t₂), . . . , x(t_N).

Метод Эйлера

Метод Эйлера – простейший метод численного интегрирования обыкновенных дифференциальных уравнений. Получается путем замены производной функции ее численной аппроксимацией:

.

Приближённые значения определяются по формуле:

.

Погрешность метода R_k имеет порядок h².

Метод Рунге-Кутты IV порядка

Порядок точность можно повысить за счет усложнения расчетной схемы. В частности во всех расчетных методах Рунге – Кутты точность повышается за счет включения в расчетную схему ряда значений функции правой части дифференциального уравнения в промежуточных точках расчетного шага .

Для метода Рунге – Кутты четвёртого порядка получаются следующие расчетные формулы:

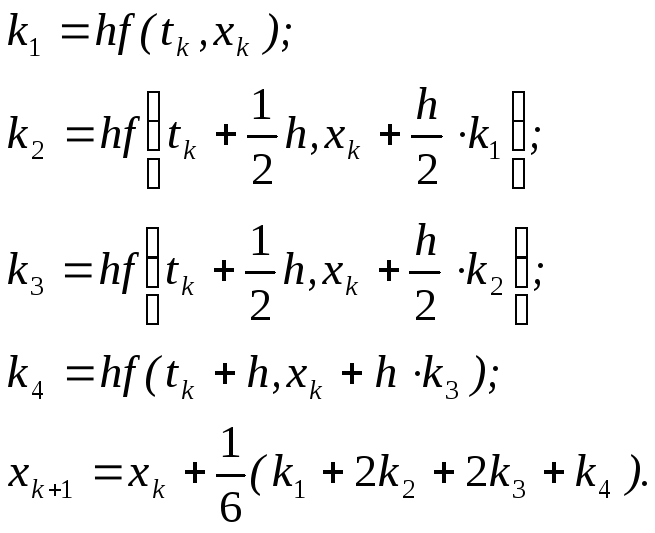
При вычислениях по приведённым формулам сначала последовательно находятся k₁, k₂, k₃, k₄, а затем определяется x_k+1.

Формулы Рунге – Кутты m-го порядка (m> 2) имеют погрешность порядкаh^m+1.

Явный многошаговый метод Адамса

В методах Рунге-Кутта значение зависело только от информации в предыдущей точке. Кажется вполне очевидным, что можно добиться большей точности, если использовать информацию о нескольких предыдущих точках. Именно так работают многошаговые методы.

Большой и важный класс многошаговых методов возникает на основе следующего подхода. Если подставить в исходное дифференциальное уравнение точное решение и проинтегрировать это уравнение на отрезке, то получится следующий результат:

,

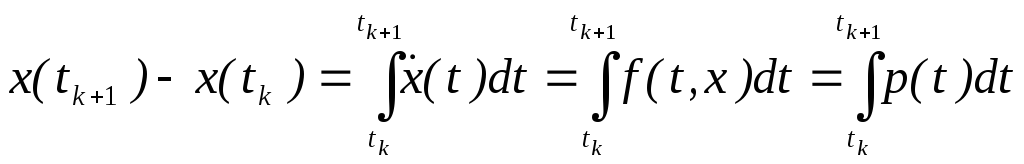где в последнем члене предполагаем, что p(t)-полином, аппроксимирующийf(x,t). Чтобы построить этот полином, предположим, чтоx_k , x_k-1 , … , x_k-n – приближения к решению в точкахt_k , t_k-1 , … , t_k-n.Gо-прежнему считаем, что узлы расположены равномерно с шагомh. Тогда(i = k, k-1, …, k-n) есть приближения к в точкахt_k , t_k-1 , … , t_k-n, и мы в качестве полиномаpвозьмём полином для набора данных(i = k, k-1, …, k-n) . Таким образом,p-полином степениn, удовлетворяющий условиям, (i = k, k-1, …, k-n) . В принципе, можно проинтегрировать этот полином явно, что ведёт к следующему методу:

.

В простейшем случае, когда n=0, полиномpесть константа, равнаяf_k, и мы получаем обычный метод Эйлера. Еслиn=1, тоpесть линейная функция, и интегрируя этот полином на, получаем следующий метод:

, (1)

который является двухшаговым, поскольку использует информацию в двух точках t_k , t_k-1. Аналогично, еслиn=2, тоpесть квадратичный полином, а соответствующий метод имеет вид:

. (2)

Если n=3, то интерполяционный полином является кубическим, а соответствующий метод определяется формулой:

(3)

Отметим, что метод (2) является трёхшаговым, а (3) -четырёхшаговым. Формулы (1)-(3) известны как явные методы Адамса (Адамса- Башфорта) , т.к. они для нахождения x_k+1 не требуют решения никаких уравнений. Метод (1) имеет второй порядок точности, поэтому его называют методом второго порядка. Аналогично, методы (2) и (3) называют соответственно методами Адамса- Башфорта третьего и четвёртого порядков.

Правило Рунге

Правило Рунге — правило оценки погрешности численных методов, было предложено К. Рунге в начале 20 века.

Основная идея (для методов Рунге-Кутты решения обыкновенных дифференциальных уравнений) состоит в вычислении приближения выбранным методом с шагом h, а затем с шагомh/2, и дальнейшем рассмотрении разностей погрешностей для этих двух вычислений.

Для оценки погрешности численного решений обыкновенных дифференциальных уравнений на регулярных сетках требуется решить задачу на 2 сетках, один раз с шагом h() и второй — с шагомh/2(). Формула:

дает погрешность решения . Подпонимается порядок точности использованного численного метода. Например, для численного метода, имеющего четвёртый порядок точности (метод Рунге-КуттыIV), формула принимает вид:

.