2. Задачи повышенного уровня сложности.
3.31. Доказать,
что любое рациональное число можно
записать в виде десятичной периодической
дроби.
Доказать, что
следующие числа иррациональны.
3.32.
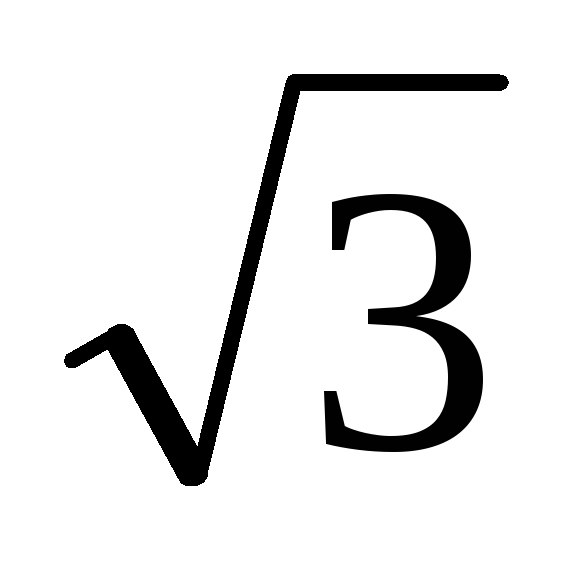 .
3.33.
.
3.33.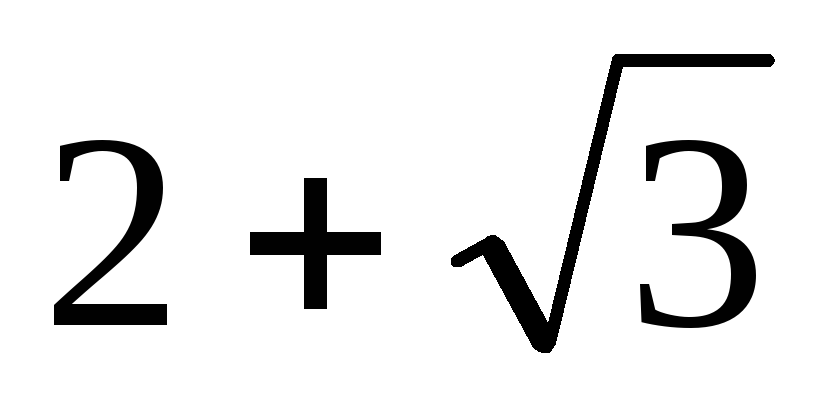 .
3.34.
.
3.34.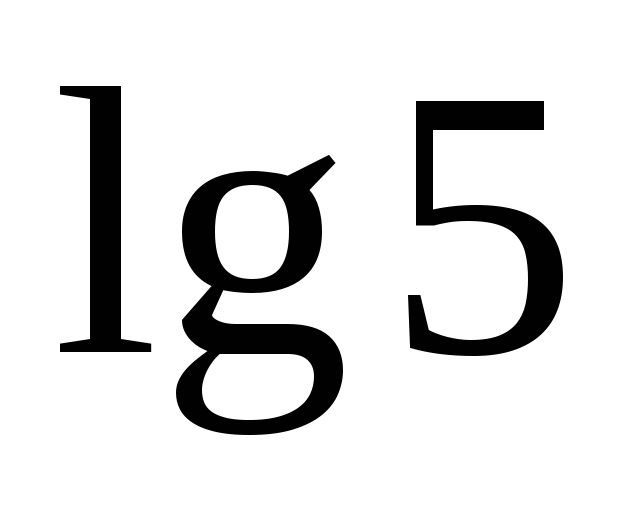 .
.
3.35. Доказать,
что для любых вещественных чисел
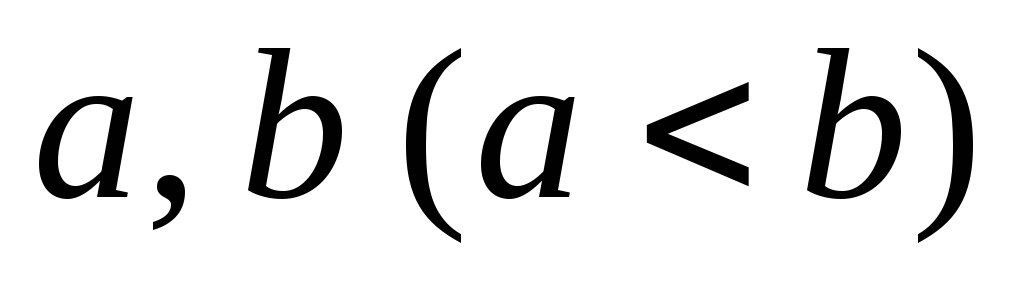 найдется рациональное число
найдется рациональное число такое, что
такое, что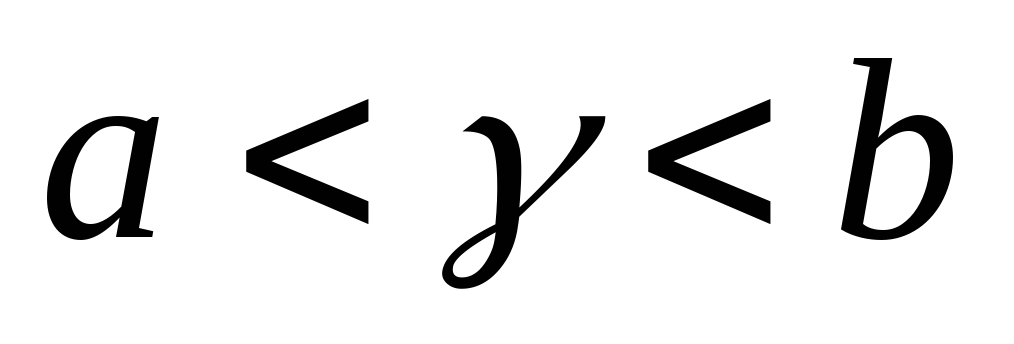 .
.
3.36.
Доказать, что для любых вещественных
чисел
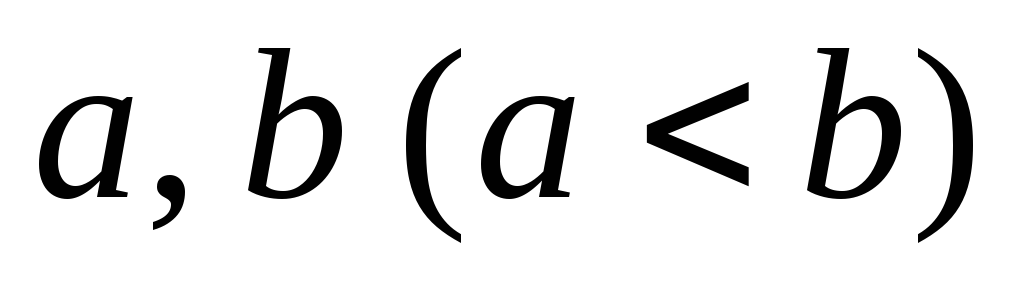 найдется иррациональное число
найдется иррациональное число такое, что
такое, что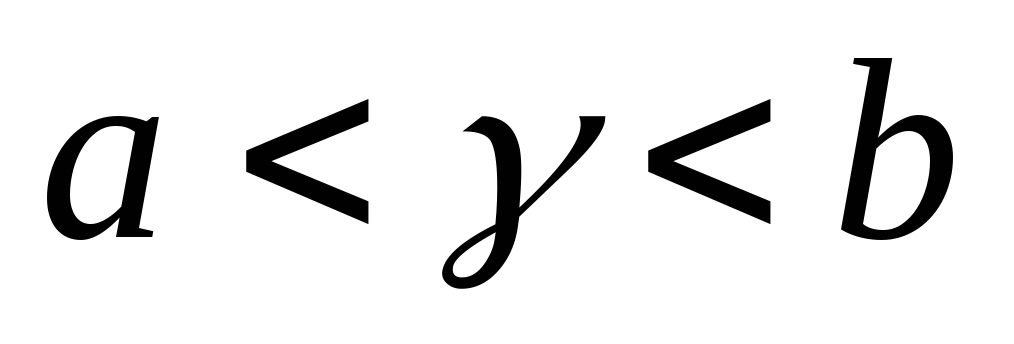 .
.
3.37. Каков порядок
подгрупп групп 7-го и 10-го порядков?
Построить таблицу умножения группы
седьмого порядка.
3.38. Построить
таблицу умножения группы диэдра
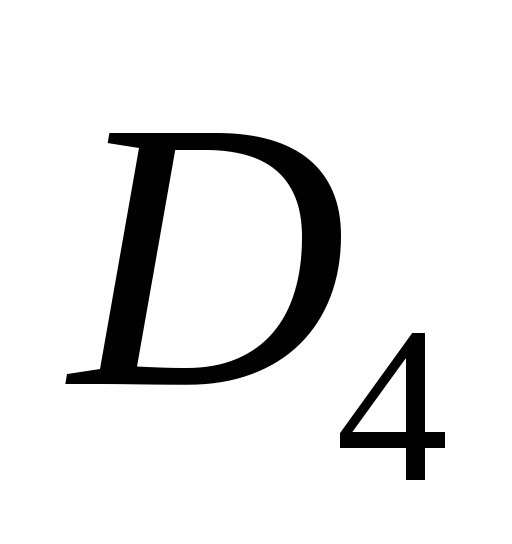 .
Эту группу можно рассматривать как
группу симметрии квадрата относительно
его поворотов на углы
.
Эту группу можно рассматривать как
группу симметрии квадрата относительно
его поворотов на углы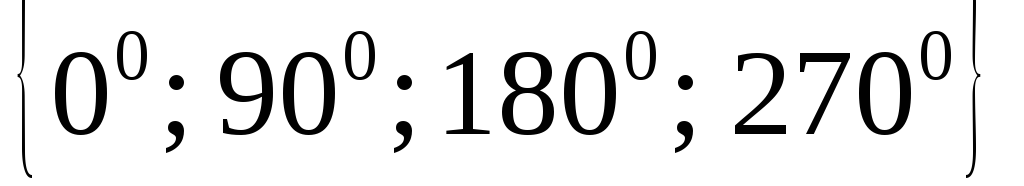 вокруг оси, перпендикулярной плоскости
квадрата и проходящей через его центр,
а также поворота квадрата на угол
вокруг оси, перпендикулярной плоскости
квадрата и проходящей через его центр,
а также поворота квадрата на угол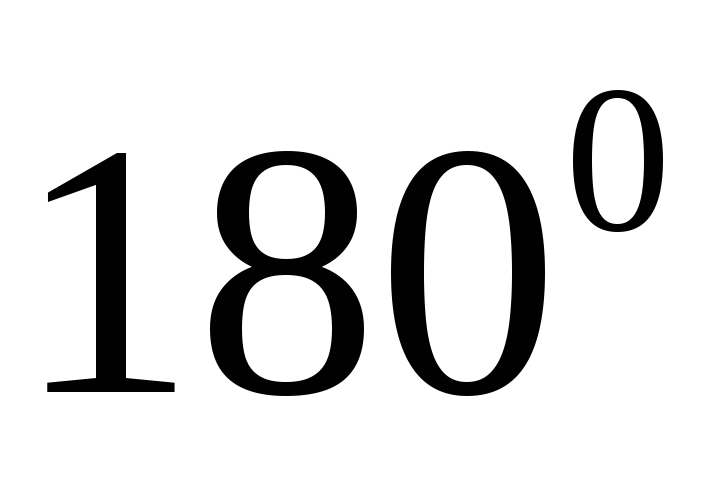 относительно оси, лежащей в плоскости
квадрата, проходящей через его центр и
параллельной стороне квадрата. Найти
подгруппы этой группы. Построить
факторгруппу
относительно оси, лежащей в плоскости
квадрата, проходящей через его центр и
параллельной стороне квадрата. Найти
подгруппы этой группы. Построить
факторгруппу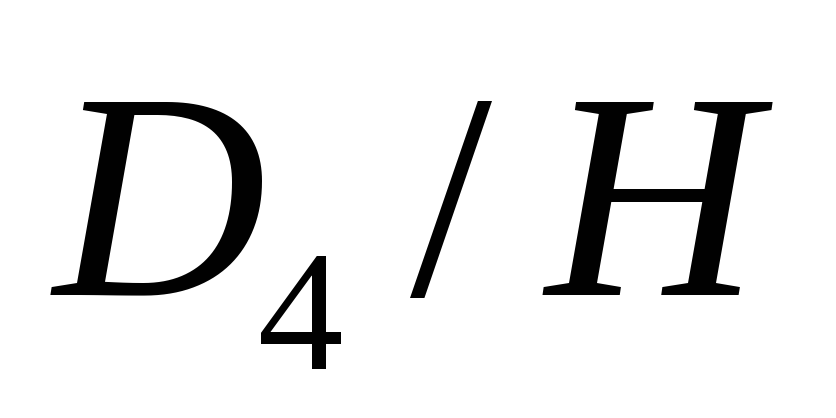 ,
доказав предварительно инвариантность
,
доказав предварительно инвариантность ,
где
,
где - подгруппа четвертого порядка. Построить
гомоморфизм
- подгруппа четвертого порядка. Построить
гомоморфизм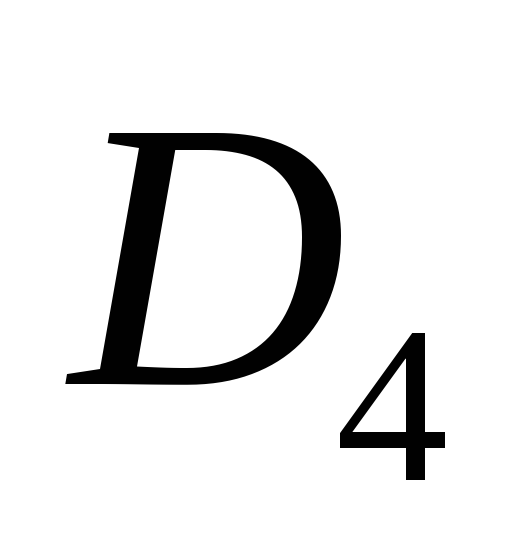 на
на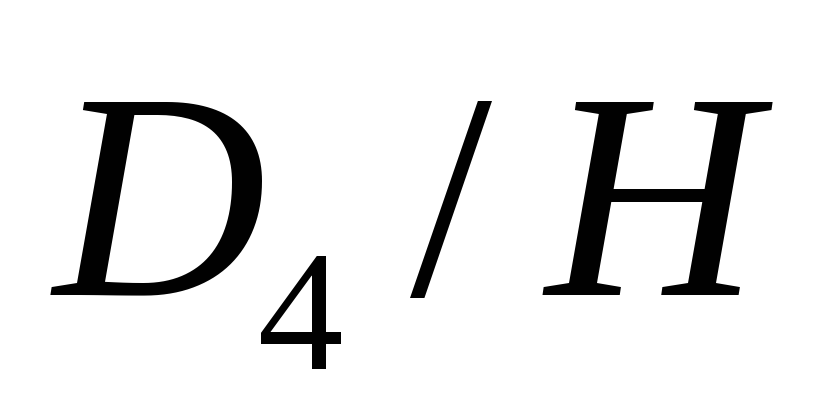 .
Какой подгруппе симметрической группы
.
Какой подгруппе симметрической группы изоморфна группа диэдра
изоморфна группа диэдра ?
?
3.39. Построить
таблицу умножения группы кватернионов
 ,
содержащей элементы
,
содержащей элементы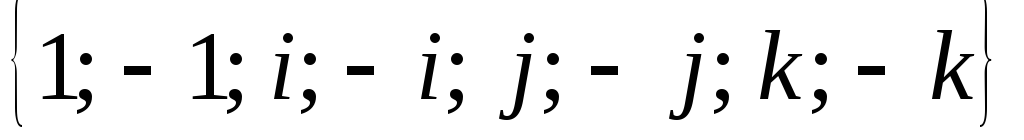 .
Учесть, что
.
Учесть, что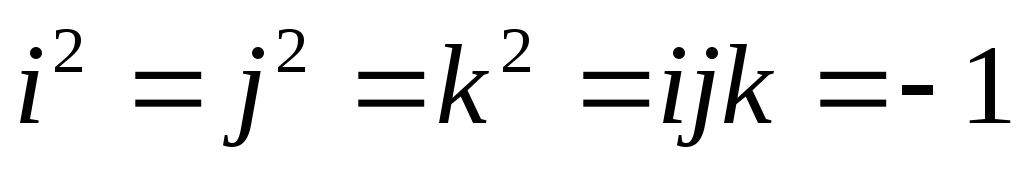 .
Найти левые и правые смежные классы
подгруппы
.
Найти левые и правые смежные классы
подгруппы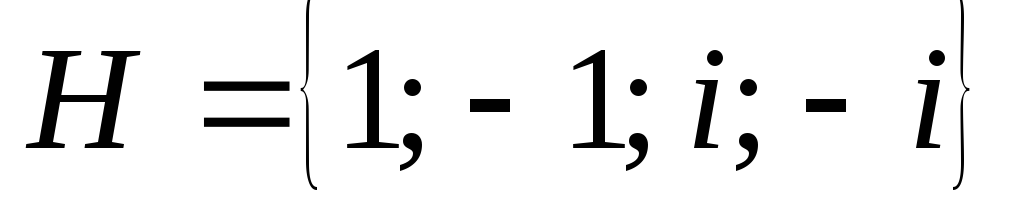 в группе кватернионов. Является ли эта
подгруппа инвариантной? В случае
положительного ответа построить
факторгруппу
в группе кватернионов. Является ли эта
подгруппа инвариантной? В случае
положительного ответа построить
факторгруппу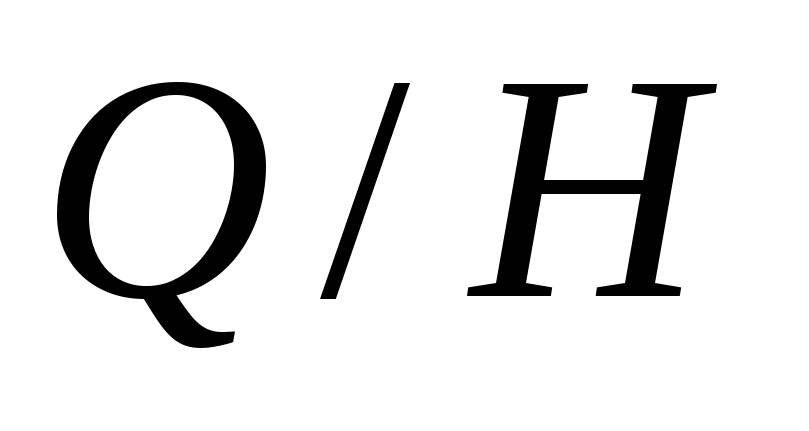 ,
задав ее таблицей умножения. Какие еще
подгруппы имеет группа кватернионов?
,
задав ее таблицей умножения. Какие еще
подгруппы имеет группа кватернионов?
3.40. Найти все
собственные подгруппы группы кватернионов
 .
Описать все сопряженные подгруппы
подгруппе
.
Описать все сопряженные подгруппы
подгруппе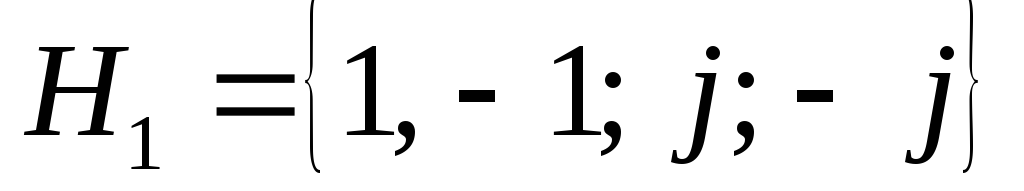 в группе
в группе .
Доказать, что подгруппа
.
Доказать, что подгруппа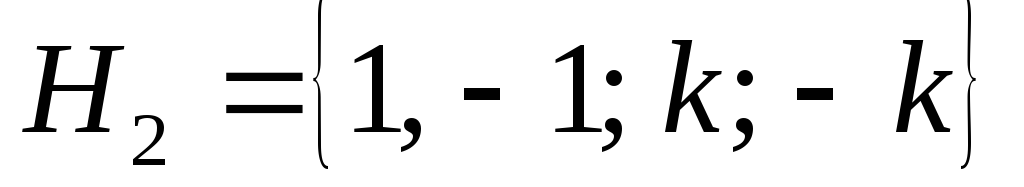 является нормальным делителем и найти
факторгруппу
является нормальным делителем и найти
факторгруппу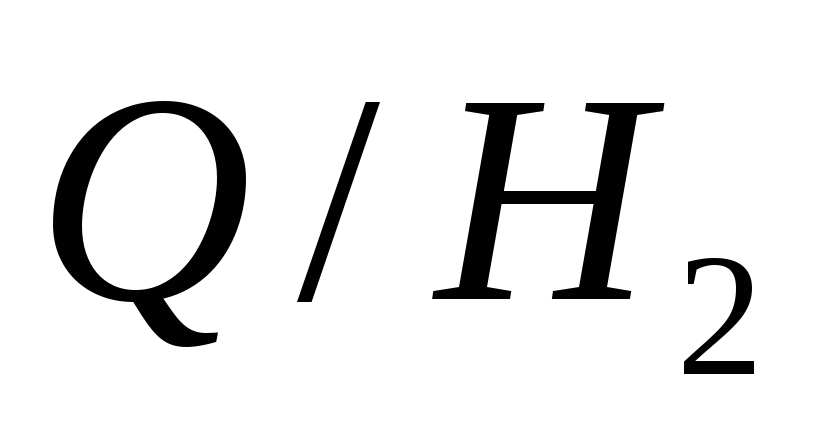 с ее таблицей умножения.
с ее таблицей умножения.

