
- •Московский государственный строительныйуниверситет
- •§ 2. Определители второго и третьего порядков.
- •§ 3. Определители n-ого порядка.
- •§4. Свойства определителей.
- •§5. Алгебра матриц.
- •Свойства суммы матриц и произведения матрицы на число.
- •Свойства умножения матриц.
- •§6. Обратная матрица.
- •§ 7. Ранг матрицы.
- •Глава 2. Системы линейных уравнений.
- •§1. Основные понятия.
- •§2. Матричная запись системы линейных уравнений.
- •§ 3. Решение системы линейных уравнений методом Крамера.
- •§ 4. Решение систем линейных уравнений с помощью обратной матрицы.
- •§ 5. Метод Гаусса.
- •§ 6. Теорема Кронекера – Капелли.
- •§ 7. Однородные системы линейных уравнений.
- •Примеры.
- •Глава 3. Примеры. Задание 1.
- •Задание 2.
- •Найти: а) ; б) ; в) ; г) ; д) .
- •Задание 3.
- •Ответ: , , .
- •Ответ: , , .
- •Задание 4.
- •Оглавление.
Задание 2.
Даны матрицы:
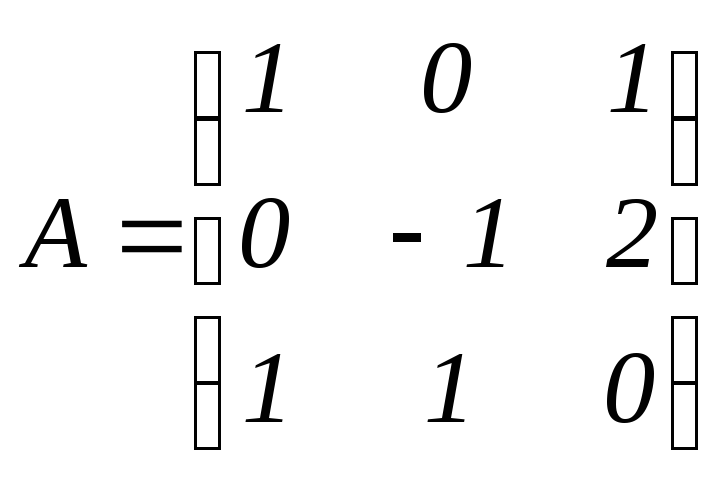 ,
,
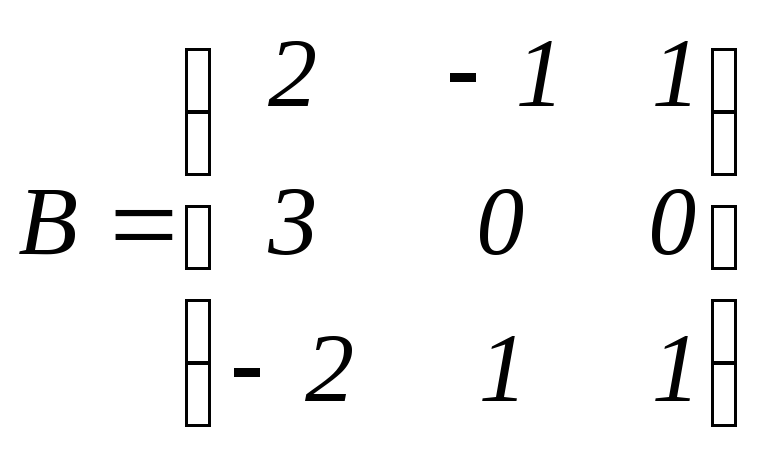 ,
,
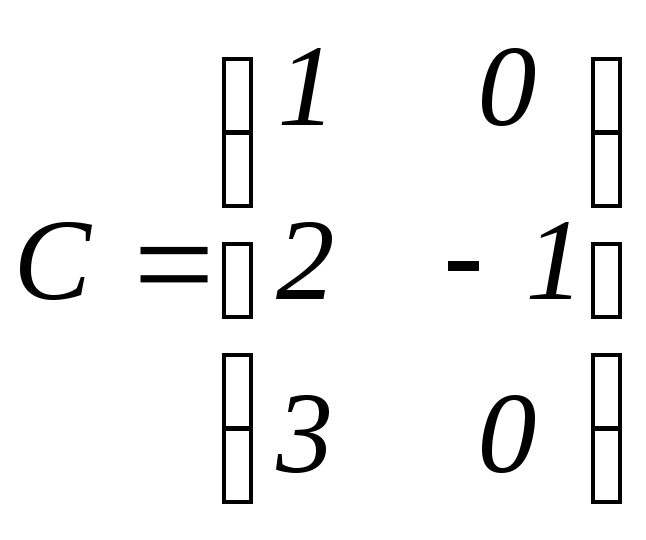 .
.
Найти: а) ; б) ; в) ; г) ; д) .
Решение.
а)
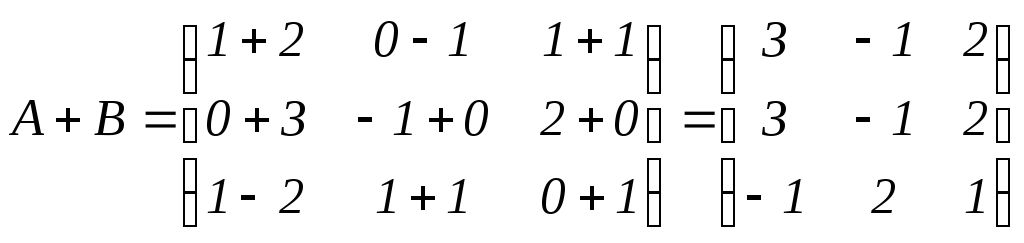 .
.
б)
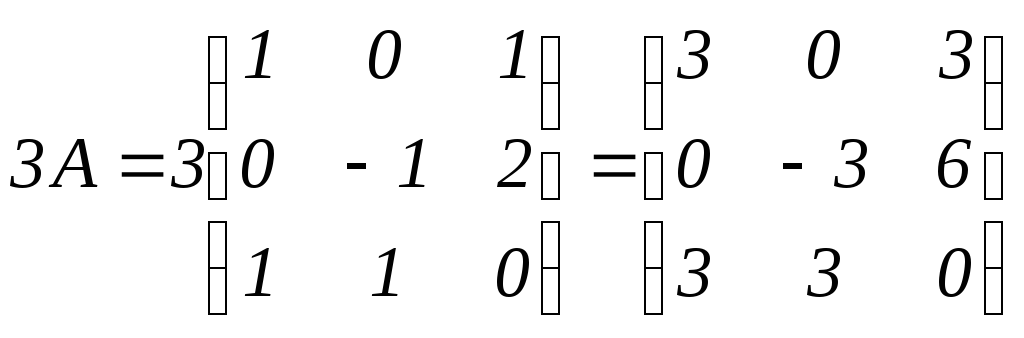 .
.
в)
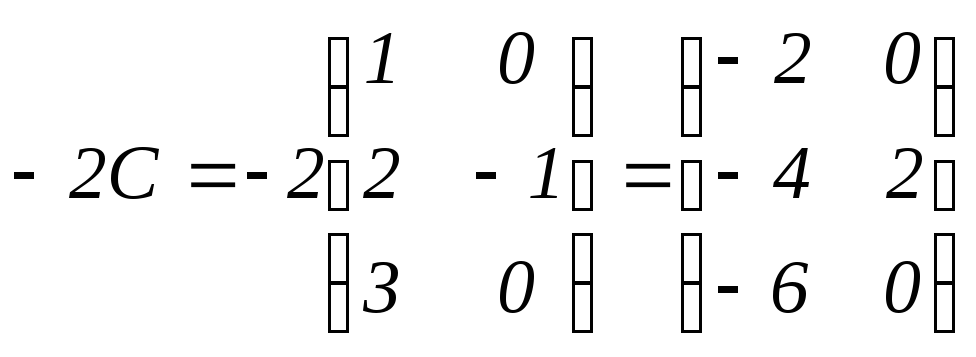 .
.
г)
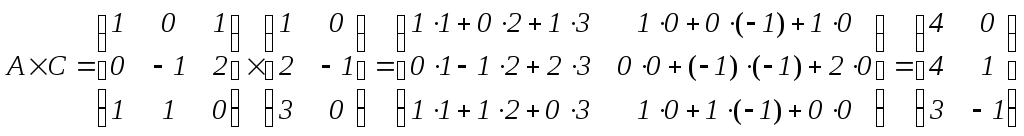 .
.
д)
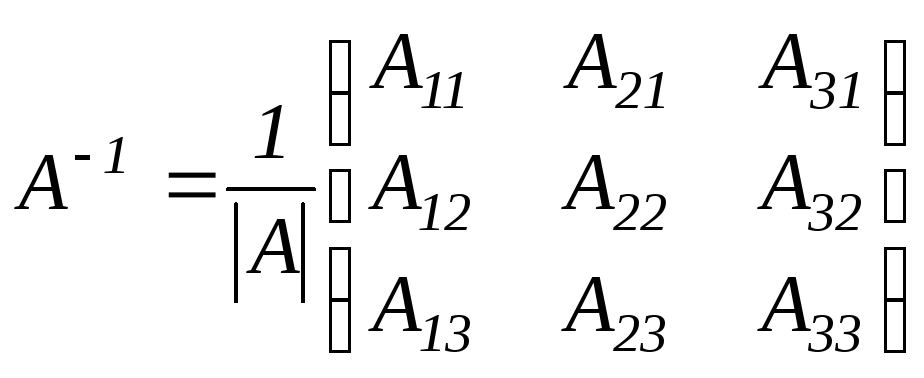 .
.
Найдем определитель матрицы A:

следовательно, обратная матрица существует.
Определим алгебраические дополнения
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найдем
![]() (обратную матрицу к матрицеА):
(обратную матрицу к матрицеА):
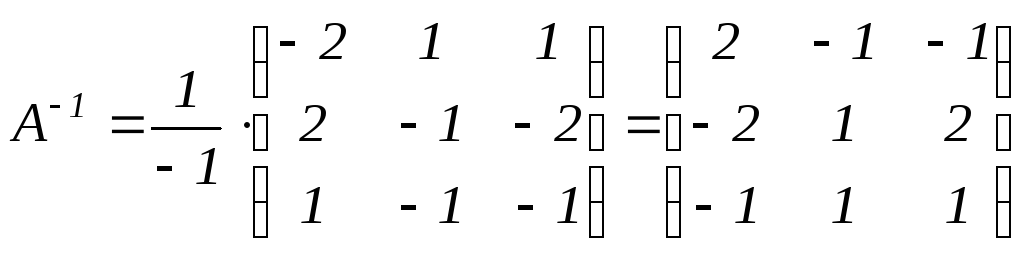 .
.
Проверка:

Задание 3.
Данасистема линейных уравнений:
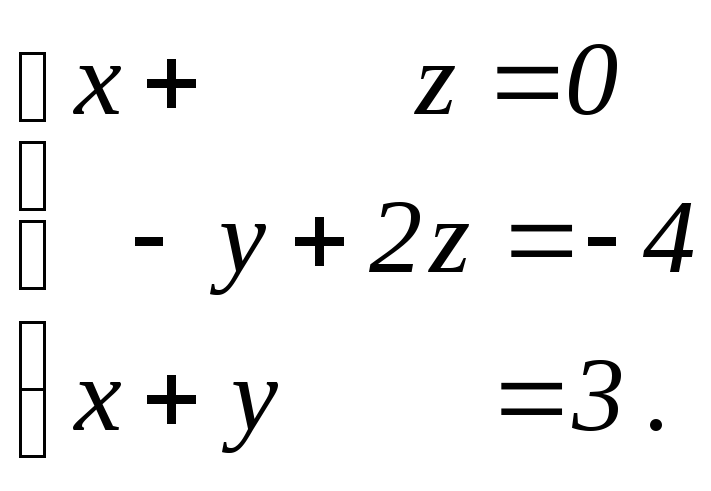
Решитьэту систему:
а) по формулам Крамера;
б) с помощью обратной матрицы;
в) методом Гаусса.
Решение.
а) Найдем определитель системы :
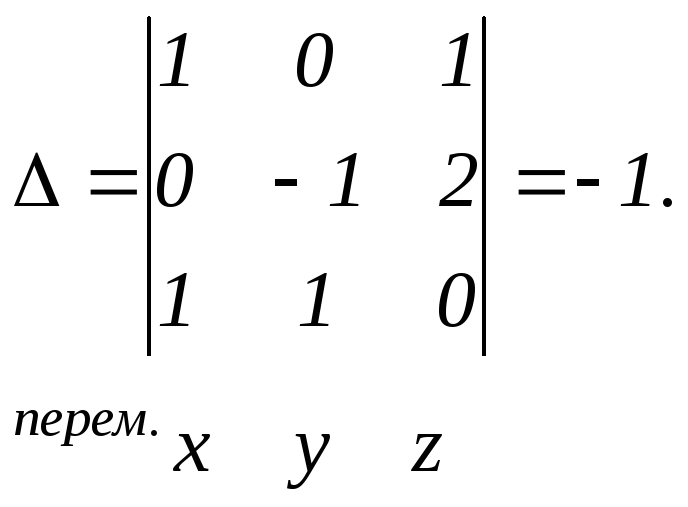
В этом определителе заменим 1- ый столбец столбцом свободных членов, получим определитель :
 .
.
Вычислим определитель, который получается из определителя системы заменой 2-ого столбца столбцом свободных членов:
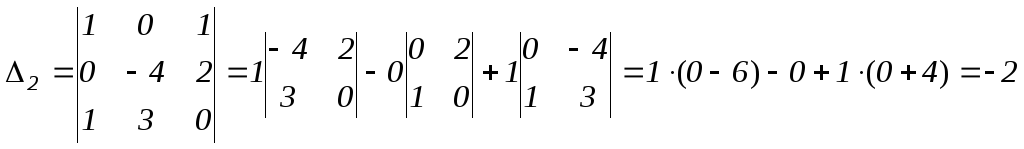 .
.
Аналогичным образом, заменяя в определителе системы 3-ий столбец столбцом свободных членов, получим :
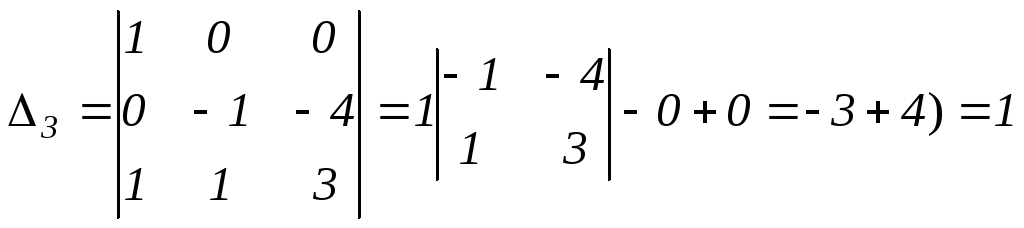 .
.
Найдем значения x, yиz по формулам Крамера:
![]() ;
;
![]() ;
;
![]() .
.
Ответ: , , .
б) Рассмотрим матрицы:
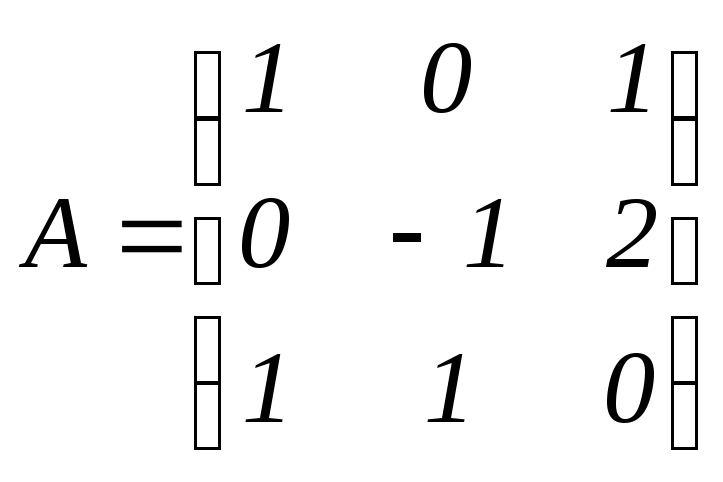 -
матрица, состоящая из коэффициентов
при неизвестных;
-
матрица, состоящая из коэффициентов
при неизвестных;
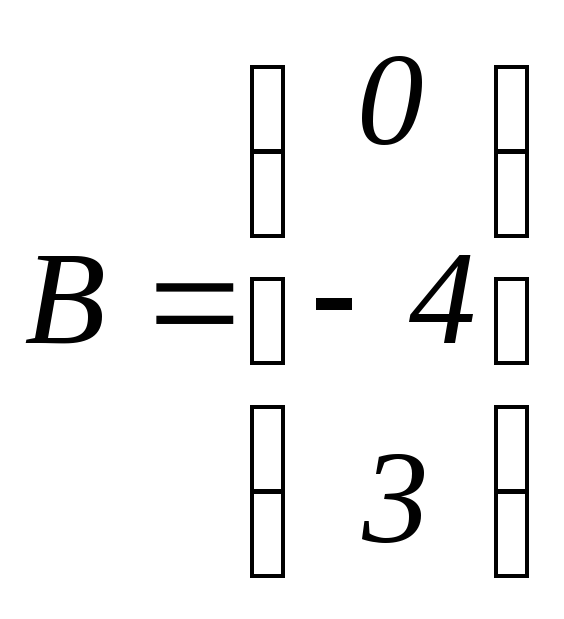 -
матрица свободных членов;
-
матрица свободных членов;
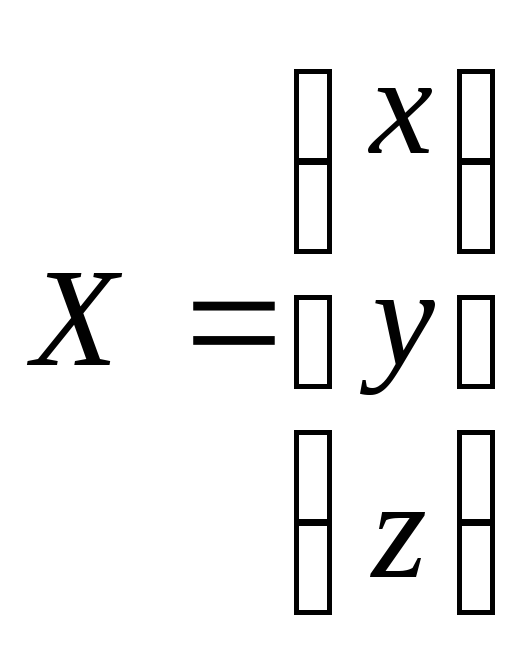 -
матрица неизвестных.
-
матрица неизвестных.
Тогда, в матричной форме система линейных уравнений может быть записана следующим образом:
![]() .
.
Если
![]() ,
то система имеет единственное решение,
которое можно найти по формуле:
,
то система имеет единственное решение,
которое можно найти по формуле:
![]() .
.
Для матрицы
![]() взадании №2 ( пункт д) нами была
найдена обратная матрица:
взадании №2 ( пункт д) нами была
найдена обратная матрица:
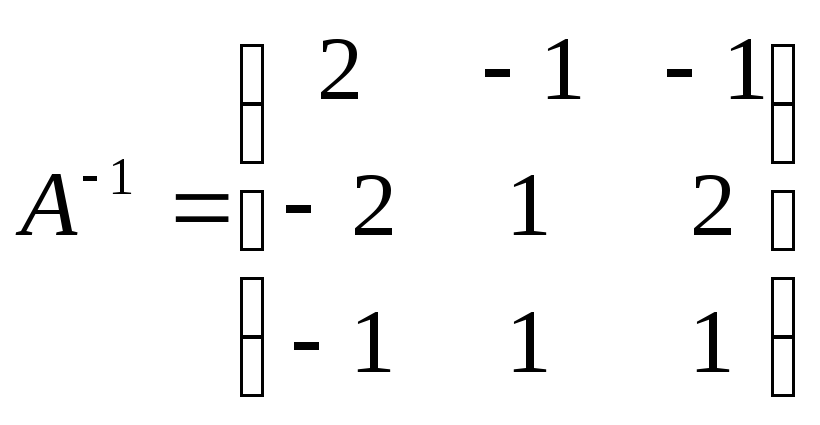 .
.
Найдем матрицу
![]() :
:
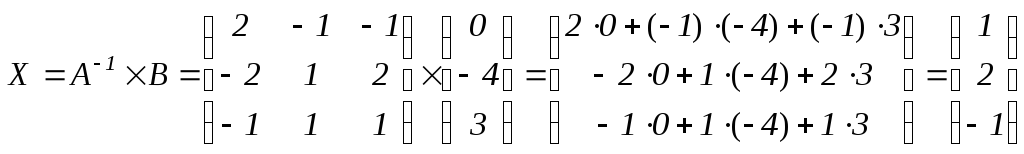 .
.
Ответ: , , .
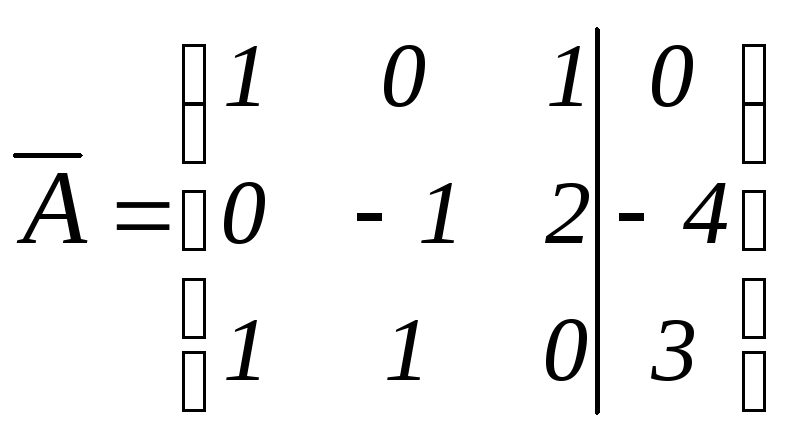
в) Выпишем расширенную матрицу системы :
 .
.
Проверяем:
 .
.Мысленно умножим элементы 1-ой строку на «-1» и сложим с элементами 3-ей строки, получим:
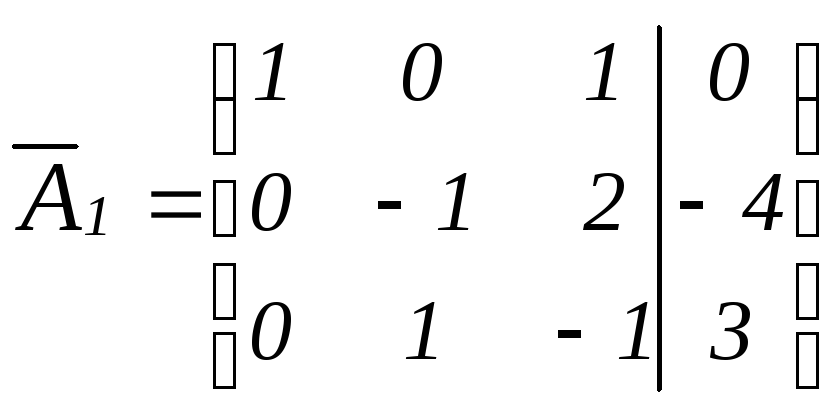 .
.
Проверяем:
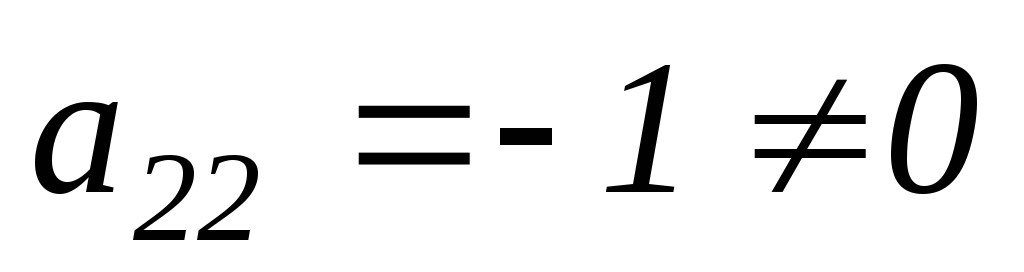 .
.Мысленно умножим 2-ую строку на «1» и сложим с 3-ей строкой:
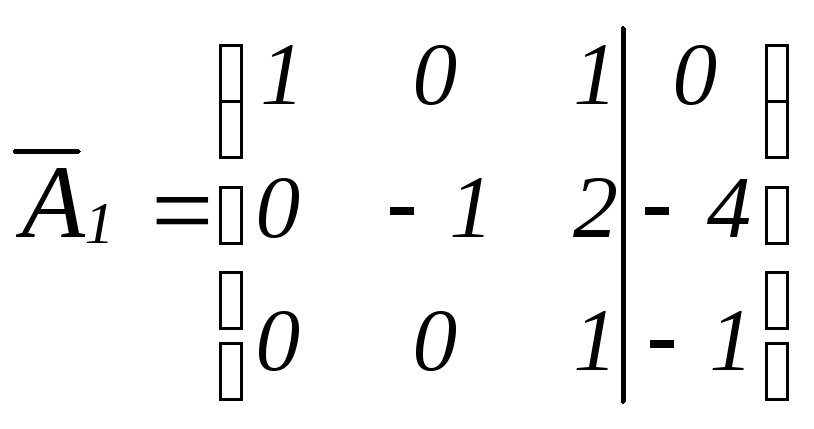 ,
,
получаем матрицу ступенчатого вида (см. определение 2 §7 главы I).
Составляем систему уравнений, соответствующую матрице
 :
:
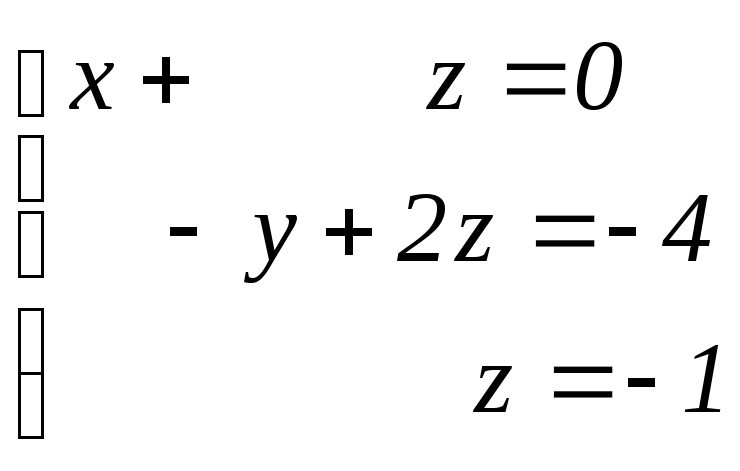 .
.
Подставляем
![]() в предпоследнее уравнение системы :
в предпоследнее уравнение системы :
![]() ,
,
отсюда
![]() .
.
Из первого уравнения находим
![]() .
.
Ответ:
 .
.
Задание 4.
Пользуясь критерием Кронекера – Капелли, исследовать систему линейных уравнений на совместность, и в случае совместности найти ее решение методом Гаусса
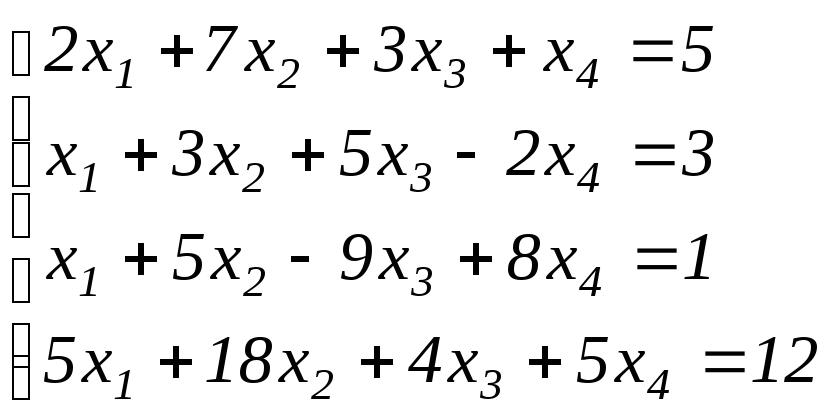 .
.
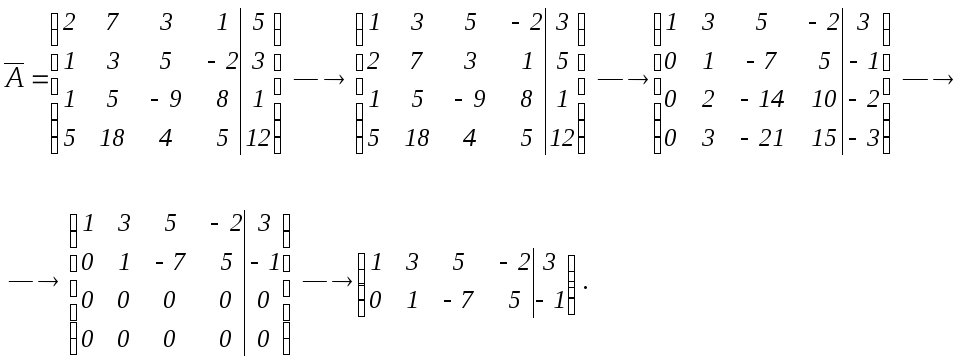
При переходе от 1-ой матрице ко 2-ой
мы поменяли местами 1-ую и 2-ую строки
для простоты вычислений, затем мысленно
умножили элементы1-ой строки на «-2»;
«-1» и «-5» и результат прибавили
соответственно к элементам 2-ой, 3-ей,
4-ой строк, получили 3-ю матрицу. Затем
перешли к 4-ой матрице: 1-ую и 2-ую строки
оставили без изменения; умножив элементы
2-ой строки на «-2», затем на «-3», прибавили
результаты умножения соответственно
к элементам 3-ей и 4-ой строк. Затем убрали
нулевые строки и перешли к матрице
ступенчатого вида. Мы одновременно
приводим к ступенчатому виду основную
и расширенную матрицы
![]() и
и
![]() .
.
По определению ранга матрицы (см. определение 3 §7 главы I)
![]() .
.
В силу критерия Кронекера – Капелли система уравнений совместна. Переходим от последней матрицы к системе уравнений:
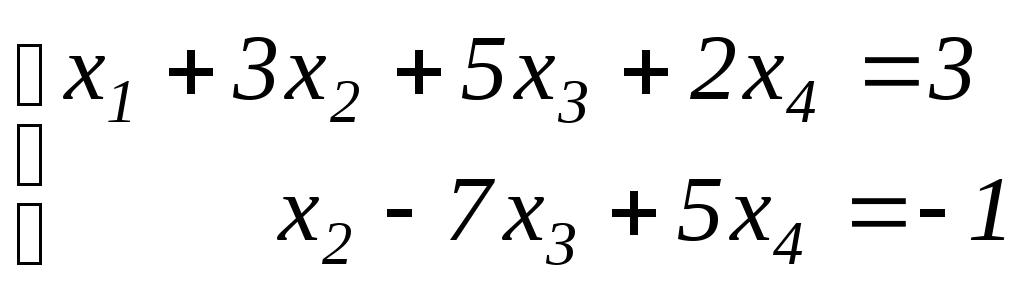 .
.
Из последнего уравнения выражаем
![]() :
:
![]() .
.
И, подставляя это равенство в первое уравнение системы, получаем:
![]() ,
,
отсюда имеем:
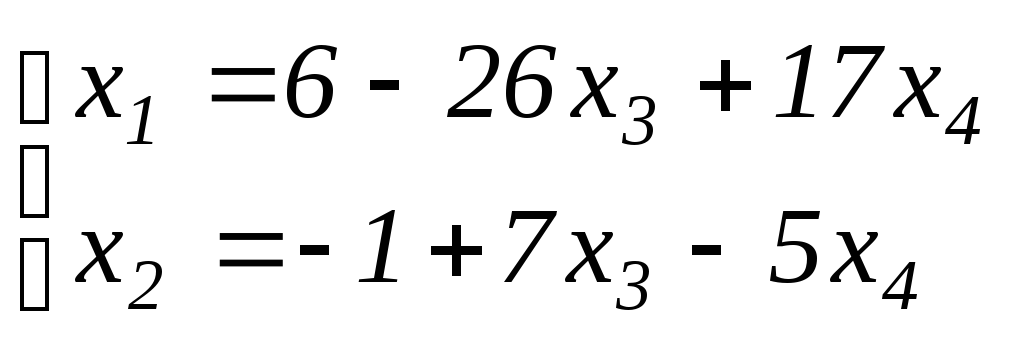 .
.
Таким образом, полученная система имеет
бесчисленное множество решений. Давая
произвольные значения независимым
переменным
![]() и
и![]() ,
мы каждый раз будем получать частные
решения системы.
,
мы каждый раз будем получать частные
решения системы.

