
- •Фбгоувпо
- •3.2 Конструирование рациональных механизмов
- •4 Кинематический анализ механизмов
- •4.1 Задачи кинематического анализа
- •4.2 Кинематика входных звеньев
- •4.3 Аналоги скоростей и ускорений
- •4.4 Определение положений звеньев и построение траекторий их точек
- •4.5 Аналитический метод исследования рычажных механизмов
- •4.6 Определение скоростей и ускорений точек методом кинематических диаграмм
- •4.7 Определение скоростей и ускорений методом планов
- •4.7.1 Построение плана скоростей и ускорений кривошипно-ползунного механизма
- •4.7.2 Построение плана скоростей и ускорений кулисного механизма
4.2 Кинематика входных звеньев
Законы движения входных звеньев могут быть заданы в аналитической или графической форме как функции времени. Например, если в аналитическом виде задано перемещение кривошипа φ(t) или ползуна s(t) (рис.4.1), то соответствующие скорости и ускорения могут быть найдены как первая и вторая производные по времени:
φ = φ(t) или s = s(t),
ω
=ω(t) или
v
= v(t)=
или
v
= v(t)= ,
,
ε
= ε(t) илиa
= a(t)=
илиa
= a(t)= .
.
Если аналитически задана, например, угловая скорость кривошипа, то по начальным условиям путем интегрирования найдем перемещение:
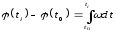 .
.
Если аналитически задано угловое ускорение кривошипа, то также по начальным условиям путем интегрирования найдем вначале угловую скорость, а затем уже перемещение:


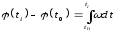 .
.

Рис.4.1 Задание координат перемещения ведущего звена
 При
графическом задании перемещения
кривошипа φ(t)
или ползуна s(t)
(рис.4.2) можно методом графического
дифференцирования получить графики и
скорости, и ускорения. Если имеются
графики скорости или ускорения
При
графическом задании перемещения
кривошипа φ(t)
или ползуна s(t)
(рис.4.2) можно методом графического
дифференцирования получить графики и
скорости, и ускорения. Если имеются
графики скорости или ускорения

Рис.4.2 Пример графического задания перемещения
ведущего звена
ведущего звена, то используя соответствующее графическое интегрирование и дифференцирование можно получить остальные кинематические характеристики. О методе графического дифференцирования и интегрирования мы еще будем говорить в соответствующих темах.
Очень часто кинематическое исследование механизма выполняют при постоянной скорости ведущего звена, что упрощает расчет. В дальнейшем при динамическом расчете уже переходят от постоянной скорости к истинной.
4.3 Аналоги скоростей и ускорений
При кинематическом
исследовании механизмов скорость и
ускорение ведомых звеньев часто удобно
выражать не в функции времени, а в функции
угла поворота
 или перемещенияs
ведущего звена. Тогда скорость и ускорение
ведомых звеньев называются соответствующими
аналогами, они не будут явно зависеть
от времени и кинематическое исследование
можно вести чисто геометрическим
способом. Это удобно ещё и потому, что
истинный закон движения ведомых звеньев
в функции времени зависит от действующих
сил и определяется при динамическом
исследовании механизмов.
или перемещенияs
ведущего звена. Тогда скорость и ускорение
ведомых звеньев называются соответствующими
аналогами, они не будут явно зависеть
от времени и кинематическое исследование
можно вести чисто геометрическим
способом. Это удобно ещё и потому, что
истинный закон движения ведомых звеньев
в функции времени зависит от действующих
сил и определяется при динамическом
исследовании механизмов.
|
Аналогом скорости и ускорения называется соответственно первая и вторая производные перемещения звена или его точки по перемещению ведущего звена. |
Для наглядности в таблице приведены выражения и для скоростей, и ускорений, и для их аналогов.
|
Параметр |
Истинное значение параметра k-того звена или m-ой точки |
Соответствующие аналоги |
|
скорость |
|
|
|
ускорение |
|
|
Найдем связь между скоростью и ускорением и аналогами скорости и ускорения в случае ведущего звена – кривошипа. Для k-того звена получим угловые характеристики:
 ;
;
 .
.
Для m-ной точки к-того звена запишем линейные характеристики:
 ;
;

Мы видим, что связь между скоростью и ускорением и аналогами скорости и ускорения в случае ведущего звена – кривошипа достаточно проста.
Здесь отметим еще одно удобство: аналоги угловых ускорений и скоростей являются безразмерными величинами, а аналоги линейных ускорений и скоростей имеют размерность длины.
В приведенных выше
формулах обозначено:
 перемещение,
скорость и ускорение ведущего звена;
перемещение,
скорость и ускорение ведущего звена;
 перемещение, скорость и ускорениеk-того
звена;
перемещение, скорость и ускорениеk-того
звена;
 перемещение, скорость и ускорениеm-ой
точки;
перемещение, скорость и ускорениеm-ой
точки;
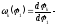 аналог угловой скорости или передаточное
отношение между звеньямиk
и 1;
аналог угловой скорости или передаточное
отношение между звеньямиk
и 1;
 аналог
углового ускорения;
аналог
углового ускорения; аналог линейной скоростиm-ой
точки;
аналог линейной скоростиm-ой
точки;
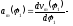 аналог
линейного ускоренияm-ой
точки.
аналог
линейного ускоренияm-ой
точки.
Заметим, что аналог угловой скорости или передаточное отношение является основной кинематической характеристикой для передаточных механизмов.
Простые аналогичные зависимости получаются и в случае, когда ведущим звеном является ползун.




