16.2. Энергетическая и дифференциальная формы уравнения движения

Уравнение движения материальной точки или звена можно представить в разном виде. Например, из теоретической механики Вам должно быть уже известно уравнение Лагранжа второго рода или уже используемое нами уравнение движения в форме ( ):

.

(16.6)

Для удобства изложения будем записывать уравнение движения для звена приведения, например, кривошипа. В этом случае изменение кинетической энергии будет иметь вид:

.

Разность работ сил движущих и сил сопротивления представим в виде:

Теперь уравнение(16.6) можно представить в виде

,

(16.7)

называемом энергетической формой уравнения движения.

Продифференцируем уравнение (16.7) по :

.

(16.8)

В этом выражении в первом слагаемом сделаем преобразования

Тогда уравнение (16.8) принимает вид:

(16.9)

Уравнение (16.9) является уравнением движения в дифференциальной форме. Здесь следует обратить внимание на то, что в первом слагаемом дифференцирование скорости происходит по времени, а во втором дифференцирование момента инерции - по углу поворота звена приведения.

точное решение путем непосредственного интегрирования.

Рассмотрим некоторые частные случаи.

1. Если моменты движущий и сопротивления и приведенный момент инерции изменяются в функции угла поворота звена приведения (или постоянны) , то уравнение движение (16.9) имеет решение в виде

.

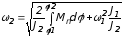2. Если моменты движущий и сопротивления и приведенный момент инерции изменяются в функции скорости звена приведения , то уравнение движение не имеет точного решения и необходимо использовать методы приближенного интегрирования (численного или графического).

3. Если моменты движущий и сопротивления изменяются в функции скорости звена приведения, а приведенный момент инерции в функции угла поворота звена приведения , то уравнение движение также не имеет точного решения и необходимо использовать методы приближенного интегрирования.

208. Толкатель А, нагруженный силою Q = 5 H, поднимается равномерно вверх силой Р = 10 H. Угол между направлением силы Р и направлением движения штанги равен α. Определить наиболь­шую величину угла α, при котором движение толкателя возможно, если коэффициент трения между толкателем А и направляющими В равен f = 0,1, а расстояние х = l.