Линейная алгебра лекция 8. Основные понятия линейной алгебры

1. Пространство Rn.

Мы уже видели, что если в трехмерном пространстве задать систему координат, то векторы однозначно представляются тройками чисел

,

и операции над векторами приводят к соответствующим операциям над тройками чисел. Во многих вопросах математики и ее приложений приходится иметь дело не с тройками, а с четверками, пятерками и т.д. действительных чисел. Например, если на складе имеется посуда в количестве 100 столовых ложек, 150 чайных ложек, 200 вилок, 50 ножей и 300 тарелок, то всю имеющуюся посуду можно описать набором чисел

x=(100, 150, 200, 50, 300).

Такой набор называется упорядоченным, т.к. набор из тех же чисел, взятых в другом порядке y=(300, 50, 100, 150, 200) соответствует другому составу посуды. Если набор посуды y привезли на склад в дополнение к имеющемуся x, то станет

x+y=(100+300, 150+50, 200+100, 50+150, 300+200) = (400, 200, 300, 200, 500),

т.е. складываются числа, стоящие в одинаковых позициях набора: первое с первым, второе со вторым и т.д.

Если 3 дня подряд завозят наборы посуды y, то всего привезли

3y=(900, 150, 300, 450, 600),

т.е. каждое число в наборе умножается на 3.

В общем случае ассортимент n видов продукции в количествах x₁, x₂, ... x_n единиц соответственно характеризуется набором

из n действительных чисел. Такие упорядоченные наборы из n чисел мы будем по-прежнему называть векторами, или n-мерными векторами. Если имеется другой вектор

,

то их сумма определяется как вектор

.

Если – число, то

.

Итак, операции сложения векторов и умножения на скаляр определяются покоординатно.

Пространством Rⁿ называется множество всех n-мерных векторов с покоординатным сложением и умножением на скаляр.

Многие другие понятия, относящиеся к Rⁿ, взяты из трехмерного пространства. Это – скалярное произведение:

;

модуль вектора:

;

расстояние между точками x и y (элементы Rⁿ мы будем называть векторами или точками в зависимости от ситуации):

.

Нулевой вектор играет роль нуля при сложении векторов:.

Коль скоро есть понятие скалярного произведения, то есть и понятие ортогональности:

.

Более того, с помощью скалярного произведения вводится понятие угла между векторами x и y:

.

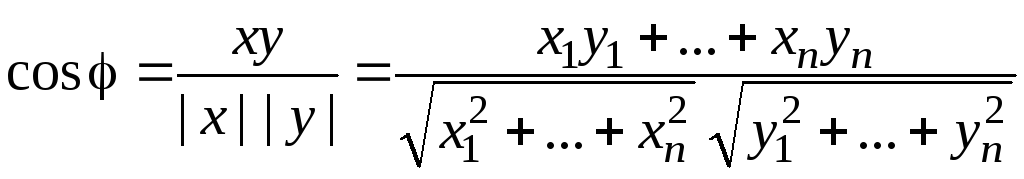Конечно, при этом надо быть уверенным, что выражение справа, взятое по модулю, не превосходит единицы, или

. (1)

Неравенство (1) действительно всегда имеет место при любых . Более того, равенство возможно в том и только в том случае, когда, т.е.х коллинеарен y. Последнее означает, что при некотором(или) и не исключает случая, когдаили (и).

Неравенство (1) имеет название: неравенство Коши–Буняковского–Шварца. Сформулируем сказанное в виде теоремы и докажем ее.

Теорема 1. Имеет место неравенство (1), причем знак «» возможен тогда и только тогда, когда .

Доказательство. Рассмотрим функцию

.

Она неотрицательна при любом t, поскольку представляет собой квадрат длины вектора (x, y выбраны произвольно, но фиксированы, t – меняется).

С другой стороны, – квадратный трехчлен относительноt с коэффициентом (y, y) при t². Поскольку он неотрицателен при всех t, то его дискриминант неположителен:

,

откуда вытекает требуемое неравенство:

.

Равенство в (1) имеет место тогда и только тогда, когда , но в этом случае трехчленимеет кореньt_:

.

Теорема 1 доказана.