
Информатика все семинары и лекции / Лекция 2
.docxЛекція № 2: Основные понятия теории информации (ПС, ЮП)
1. Предмет теории информации и основные виды информационных процессов.
Важнейшим предметом ТИ является оценка количества и качества информации. Классификация теоретических направлений в зависимости от видов информационных мер иллюстрируется на рис.1.

Рис.1.
Структурная ТИ – рассматривает дискретное построение массивов информации и ее измерение простым комбинаторным расчетом порций (квантов) информации. Наиболее часто используются количественные оценки, носящие характер геометрических, комбинаторных или аддитивных вычислений. Пример – двоичная аддитивная мера Хартли, рассмотренная на предыдущей лекции.
Статистическая ТИ – рассматривает понятие энтропии, как меры статистической (вероятностной) неопределенности информации, представленной в виде систематизированных видов сообщений. Математическим аппаратом статистической ТИ является теория вероятностей. Основоположником статистической ТИ является К.Шеннон. Эта теория является основной во всех технических приложениях информатики.
Семантическая ТИ – рассматривает ценность, полезность или сущность информации. Семантическая ТИ базируется на понятиях семиотики (науки про знаки, слова и языки).
Каждое из рассмотренных трех направлений ТИ имеет свою специфическую область применения.
Основными элементарными информационными процессами, изучаемыми ТИ, являются:
1. Восприятие информации процесс целенаправленного получения и анализа информации о каких-либо процессах, явлениях и т.д. Этапами восприятия являются:
- первичное восприятие;
- анализ объекта исследования;
- выявление и распознавание семантических признаков;
- прогнозирование ситуаций.
2. Переработка информации – это логическое, аналитическое или эвристическое преобразование информации человеком или средствами ВТ с целью наиболее эффективного ее дальнейшего использования.
3. Представление информации – это процесс преобразования ее в форму, наиболее благоприятную для восприятия и переработки человеком или техническими средствами.
4. Передача информации в пространстве или времени. Передача в пространстве между объектами информационного процесса называется телекоммуникацией. Передача во времени составляет суть процесса хранения информации.
Основной формой представления некоторой "порции" информации является сообщение. Сообщения всегда представляются в виде материально-энергетической формы, т.е. в виде символов или сигналов – материальных технических носителей информации, являющихся переменными физическими величинами. В технике известны следующие виды сигналов: электрические; электромагнитные; акустические; механические; оптические и др.
Сущность информации определяет ее основные свойства:
-
количественное содержание И;
-
качественное содержание И (ценность):
-
достоверность – степень соответствия полученной информации (данных) ее первоначальному содержанию;
-
адекватность – степень соответствия информации реальным процессам, которые она отображает;
-
полнота – как свойство достаточности для принятия решений на основе полученной информации;
-
ценность – свойство полезности содержащейся в данных информации. В динамических системах ценность является убывающей функцией времени в результате "старения" информации;
-
избыточность – свойство, обеспечивающее сохранение среднего количества информации в данных при их частичных потерях. Избыточность используется для создания методов защиты от ошибок, т.е. для повышения достоверности.
-
2. Количественное описание информации. Понятие энтропии.
Количественное описание И. является основным проблемным вопросом теории информации. Мера информации должна быть: во-первых, интуитивно понятной; во-вторых, быть объективной и удобной при расчетах.
Первая попытка измерения количества информации была предпринята в 1921 г. американским ученым Р. Хартли. Он попытался связать количество информации с числом возможных сообщений (исходов) и ввел определение логарифмической меры:
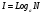 ,
,
где 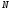 – число возможных исходов (значений)
некоторого опыта (сигнала);
– число возможных исходов (значений)
некоторого опыта (сигнала);
 – основание логарифма, измеряющего
информацию, которое определяет единицу
меры следующим образом:
– основание логарифма, измеряющего
информацию, которое определяет единицу
меры следующим образом:
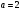 (двоичный логарифм)– единица измерения
Бит (Binary
Digital);
(двоичный логарифм)– единица измерения
Бит (Binary
Digital);
 (натуральный логарифм) – единица
измерения Нат;
(натуральный логарифм) – единица
измерения Нат;
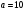 (десятичный
логарифм)– Дит (Decimal
Digital).
(десятичный
логарифм)– Дит (Decimal
Digital).
Более строгую и
объективную количественную меру
информации предложил американский
ученый Клод Элвуд Шеннон. В основополагающей
работе "Математическая теория связи"
(1948 г.) он утверждал, что семантические
аспекты неуместны для измерения
количества информации в технических
системах. Шеннон связал количественную
меру с вероятностями появления сообщений,
являющихся своеобразными информационными
квантами (порциями). При этом целесообразным
оказалось применение логарифмической
меры Хартли. Количество информации,
содержащееся в произвольном сообщении
источника, которое появляется с
вероятностью
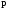 в соответствии с мерой Шеннона
в соответствии с мерой Шеннона
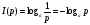 , (1)
, (1)
где
 – основание логарифма, как и ранее
определяющее единицу измерения
информации. В современной теории
информации и информатике используется,
в основном, логарифм по основанию 2,
поэтому наиболее привычной является
единица измерения информации, называемая
Битом.
– основание логарифма, как и ранее
определяющее единицу измерения
информации. В современной теории
информации и информатике используется,
в основном, логарифм по основанию 2,
поэтому наиболее привычной является
единица измерения информации, называемая
Битом.
Основными свойствами количественной меры (1) являются:
1. Непрерывность


Действительно,
если вероятность события (сообщения)
равна 1 (известное сообщение), в соответствии
с (1) количество информации равно 0. Если
вероятность сообщения
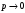 ,
то
,
то
 .
Это свойство количественной меры
иллюстрируется графиком:
.
Это свойство количественной меры
иллюстрируется графиком:
2. Аддитивность:
количество информации, получаемой от
 независимых источников, равно сумме
количества информации, получаемой от
каждого из этих источников:
независимых источников, равно сумме
количества информации, получаемой от
каждого из этих источников:
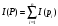 .
.
Покажем это на
примере двух (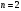 )
независимых сообщений, имеющих вероятность
совместного появления
)
независимых сообщений, имеющих вероятность
совместного появления
 .
Действительно:
.
Действительно:
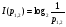 ,
однако, из теории вероятностей известно,
что вероятность появления двух независимых
событий равна произведению их вероятностей,
т.е.
,
однако, из теории вероятностей известно,
что вероятность появления двух независимых
событий равна произведению их вероятностей,
т.е.
 .
Поэтому
.
Поэтому
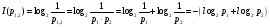
 .
.
Обобщенной
характеристикой информативности
произвольного источника информации
(сообщений) или некоторого потока данных
является энтропия,
которая определяется, как математическое
ожидание количества информации в
произвольном сообщении. Если источник
может выдавать
 различных сообщений с вероятностями
различных сообщений с вероятностями
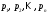 ,
соответственно, то энтропия такого
источника определяется:
,
соответственно, то энтропия такого
источника определяется:
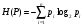 . (2)
. (2)
Понятие энтропии
заимствовано из термодинамики. Так
энтропия Больцмана характеризует
степень неопределенности некоторого
объема газа, возникающую в результате
хаотического теплового движения молекул.
Формула (2) показывает, что энтропия
является функцией только от распределения
вероятностей появления различных
сообщений источников
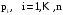 .
С использованием определения энтропии,
количество информации в произвольном
сообщении может быть определено, как
убывание степени неопределенности
источника, т.е.
.
С использованием определения энтропии,
количество информации в произвольном
сообщении может быть определено, как
убывание степени неопределенности
источника, т.е.
 ,
,
где
 – априорная (до опыта) энтропия
(неопределенность);
– априорная (до опыта) энтропия
(неопределенность);
 – апостериорная
(после опыта) степень неопределенности.
– апостериорная
(после опыта) степень неопределенности.
Пример.
Пусть учебная дисциплина подразумевает
прослушивание 8 лекций, в случае если
студент прослушал только 7 лекций, то
количество полученной им информации
может быть оценено, как убыль степени
неопределенности
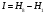 :
:
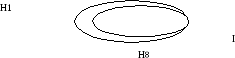
Основные свойства энтропии:
1. Непрерывность и ограниченность: энтропия любого источника информации – непрерывная величина, ограниченная в диапазоне
 ,
,
где
 – число различных сообщений источника,
называемое мощностью
алфавита
источника.
– число различных сообщений источника,
называемое мощностью
алфавита
источника.
2. Энтропия принимает
максимальное значение, если сообщения
являются взаимно независимыми и
равновероятными. Действительно, при
равновероятных сообщениях
 ,
,
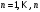 .
Тогда
.
Тогда
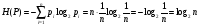
Это значит, что
мера Хартли является частным случаем
меры Шеннона для равновероятных
сообщений.
Пример: энтропия
двоичного источника.
Пусть
источник может генерировать два сообщения
 с вероятностью
с вероятностью
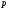 и
и
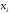 – с вероятностью
– с вероятностью
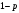 .
Тогда
.
Тогда
 при
при
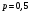 .
.
3. Энтропия детерминированных (известных) сообщений, а также энтропия невозможных сообщений равна нулю:
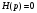 при
при
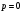 и
и
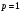 .
.
4. Свойство аддитивности. совместная энтропия независимых сообщений равна сумме их энтропий. Это свойство, также как аналогичное свойство количества информации является следствием логарифмического измерения: логарифм произведения равен сумме логарифмов:
 .
.
(далее выдача заданий на КР)
