Информатика все семинары и лекции / Лекция 3

Лекція № 3 Данные и работа с ними. (ПС, ЮП)

1. Системы счисления

Наиболее удобным средством представления информации, с точки зрения автоматизации процессов ее обработки, является язык чисел. Любой язык чисел определяется системой счисления.

Система счисления – способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.

Различают непозиционные и позиционные системы счисления.

В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе. Тем самым исключается всякая возможность автоматизации распознавания чисел и, как следствие, обработки информации.

В позиционной системе счисления значение каждой цифры зависит от ее места (позиции) в числе.

Позиционные системы счисления характеризуются:

• основанием 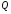системы счисления – количеством различных символов, используемых для изображения чисел. Значения этих символов лежат в пределах от 0 до ;

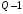• разрядом – позицией, занимаемой отдельным символом в изображении числа. Разряды нумеруются справа налево, начиная с 0;

• весом разряда – количественным значением одной единицы разряда. Численно вес разряда определяется через основание системы счисления и номер 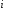разряда: .

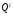Таким образом, максимальное целое число, которое может быть представлено в 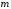разрядах числа в -ичной системе счисления – 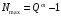. Минимальное значащее (не равное 0) число, которое можно записать в разрядах дробной части – 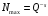. Тогда, имея в целой части числа 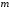, а в дробной разрядов, можно представить 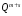чисел из диапазона от 0 до .

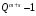Поскольку в технике известно много физических приборов и сред с двумя устойчивыми состояниями, в качестве алфавита языка ЭВМ приняты символы 0 и 1, названные двоичными цифрами. Последовательности нулей и единиц конечной длины образуют двоичные числа, которые, в свою очередь, образуют позиционную двоичную систему счисления.

2. Кодирование чисел в ЭВМ.

Для кодирования (представления, хранения и транспортировки) данных в ЭВМ используются различные коды.

Кодом называется некоторая система символов, составляющих алфавит, и совокупность правил использования этого алфавита.

Наиболее типичным и, возможно, первым примером использования кода является письменность, как средство представления (кодирования) информации (данных) с использованием материальных носителей.

В технических системах, как уже отмечалось, наибольшее распространение получил двоичный числовой код. Это связано с необходимостью сделать язык общения технических систем как можно более примитивным. Каждая из значащих цифр кода может принимать только два значения: "1" или "0". В некоторых языках программирования для представления машинных команд и данных используются восьмеричная и шестнадцатеричная системы счисления. Все системы счисления (кодирования) однозначно связаны между собой. Данные, представленные в одном коде, без особого труда могут быть трансформированы (переведены)в другой код. Этот процесс принято называть кодированием данных. (Пример – текстовые документы, переводимые с одного языка на другой).

Рассмотрим цифровое кодирование при использовании различных алфавитов. В различных системах используются следующие символы для кодирования значений отдельных разрядов чисел:

Система счисления	Алфавит
Десятичная СС	0,1,2,3,4,5,6,7,8,9.
Двоичная СС	0,1.
Восьмеричная СС	0,1,2,3,4,5,6,7.
Шестнадцатеричная СС	0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

Как выглядят одни и те же числа в различных системах счисления?

Система счисления
Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
3	11	3	3
9	1001	11	9
15	1111	17	F

Правило перевода целых чисел из одной системы счисления в другую:

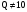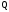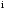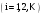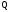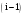Целые десятичные числа кодируются числами системы счисления с основанием путём последовательного деления десятичного числа на до тех пор, пока частное не окажется меньше . Остаток от -го деления при использовании символов -ичной системы счисления заносится в -й разряд формируемого числа. Последнее частное образует старший (левый) разряд 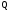-ичного числа.

Рассмотрим это правило на примере, представив десятичное число 154 в двоичной форме:

154 2

0 77 2

1 38 2

0 19 2

1 9 2

1 4 2

0 2 2

0 1

1

Следовательно, 154₁₀=10011010₂.

Для возврата записи числа из произвольной системы счисления в десятичную используется понятие "веса значащего разряда" 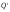. Например, для рассмотренного примера:

.

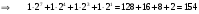Правило перевода дробных чисел из одной системы счисления в другую:

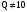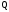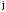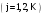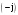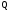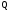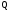Дробная часть десятичных чисел представляется в системе счисления с основанием путём последовательного умножения на . При этом целая часть -го произведения заносится в -й разряд дробной части -ичного числа, а оставшаяся дробная часть произведения вновь умножается на и т.д. Указанная процедура повторяется до тех пор, пока не будет обеспечено достаточное количество цифр (точность) -ичного числа или дробная часть не станет равной нулю.

Пример:

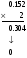
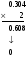
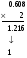
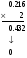
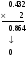
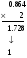
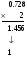
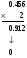и т. д.

Значит 0.152₁₀ ≈ 0.00100110₂.

Проверим правильность результата путем обратного преобразования:

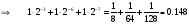
Задание на самостоятельную проработку: запишите десятичные числа 22, 148, 1.25 в двоичной системе счисления.