
Aнтенны и распространение радиоволн
.pdf
|
|
|
|
|
|
|
3. ЭЛЕМЕНТАРНАЯ РАМКА С ТОКОМ |
|
|
|
|
|
|
13 |
|||||||||||||||||||
Векторный потенциал, создаваемый в точке P малым участком витка углового размера |
|||||||||||||||||||||||||||||||||
dϕ0, расположенным в точке Q, равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dA~ = |
1 |
~e |
|
I(t − R(ϕ0)/c) |
a dϕ0 = |
1 |
|
( ~e |
sin ϕ0 |
+ ~e |
|
cos ϕ0) |
|
I(t − R(ϕ0)/c) |
a dϕ0. |
|
|||||||||||||||||
|
|
|
|
|
4π |
|
|
|
|
|
|||||||||||||||||||||||
|
4π |
ϕ |
R(ϕ0) |
|
|
|
|
|
|
− x |
|
|
|
|
|
y |
|
|
|
|
|
R(ϕ0) |
|
||||||||||
Векторный потенциал, создаваемый всем витком, определяется интегралом |
|
||||||||||||||||||||||||||||||||
|
|
|
|
1 |
Z0 |
2π |
|
|
|
|
|
|
|
|
|
|
|
I(t |
|
|
R(ϕ |
)/c) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
A~ = |
|
(−~ex sin ϕ0 + ~ey cos ϕ0) |
|
|
− 0 |
|
|
|
a dϕ0. |
(1.39) |
|||||||||||||||||||
|
|
|
|
4π |
|
|
R(ϕ0) |
|
|
|
|||||||||||||||||||||||
Несложно убедиться, что R(ϕ0) = |
|
|
|
|
|
|
|
|
|
|
. Если радиус витка |
||||||||||||||||||||||
|
r2 + a2 |
− |
2ar sin ϑ cos(ϕ |
0 − |
ϕ) |
||||||||||||||||||||||||||||
мал по сравнению с расстоянием r, то p |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.40) |
|||||||||||||||||||
и |
|
|
|
|
|
R(ϕ0) ≈ r − a sin ϑ cos(ϕ0 − ϕ) |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
≈ |
|
h1 + |
|
|
sin ϑ cos(ϕ0 − ϕ)i . |
|
|
|
|
|
|
(1.41) |
|||||||||||||
|
|
|
|
|
|
R(ϕ0) |
r |
r |
|
|
|
|
|
|
|||||||||||||||||||
Взяв первые два члена разложения функции I(t) в ряд Тейлора и используя (1.40),
получим
I(t − R(ϕ0)/c) ≈ I(t − r/c) + I0(t − r/c) ac sin ϑ cos(ϕ0 − ϕ).
Подстановка этого выражения совместно с (1.41) в (1.39) даст векторный потенциал витка в виде
|
|
|
A~ = 4π |
( |
|
−r |
|
|
|
|
|
|
|
2π |
(−~ex sin ϕ0 |
+ ~ey cos ϕ0) h1 + r sin ϑ cos(ϕ0 |
− ϕ)i dϕ0 |
+ |
||||||||||||||||||||||||||||
|
|
|
t |
|
|
) Z0 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
I |
|
r/c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
I0(t − r/c) |
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
||||||
+ |
|
sin ϑ |
|
|
|
|
|
( ~e |
|
sin ϕ0 + ~e |
|
|
cos ϕ0) cos(ϕ0 |
− |
ϕ) |
1 + |
|
sin ϑ cos(ϕ0 |
− |
ϕ) dϕ0. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
4π |
|
r |
|
|
|
|
|
Z0 |
|
|
|
|
− x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
h |
r |
|
i |
||||||||||||
Выполнив интегрирование, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A~ = ~e |
|
|
a2 |
|
I(t − r/c) |
+ |
|
I0(t − r/c) |
|
sin ϑ. |
|
|
(1.42) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ϕ 4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
rc |
|
|
|
|
|
|
|
|
||||||||||||
Компоненты вектора напряжённости магнитного поля найдём по формуле (A.5): |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
= |
|
a2 |
I(t − r/c) + |
I0(t − r/c) |
cos ϑ, |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.43) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
r3 |
|
|
|
|
|
|
|
r2c |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
H |
|
= |
a2 |
|
|
I(t − r/c) |
+ |
|
I0(t − r/c) |
+ |
I00(t − r/c) |
|
|
sin ϑ, |
|
(1.44) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ϑ |
|
|
|
|
|
|
r3 |
|
|
|
|
|
r2c |
|
|
|
|
|
|
rc2 |
|
|
|
||||||||||||||
Hϕ = 0.
Для нахождения напряжённости электрического поля, как и в случае диполя Герца, подставим значения компонент вектора напряжённости магнитного поля (1.42) и (1.43) в
(A.1), что даст |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ε |
∂Er |
|
= 0, |
ε |
∂Eϑ |
= 0, |
ε |
∂Eϕ |
= |
|
a2 |
|
I000 |
(t − r/c) |
|
+ |
I00(t − r/c) |
sin ϑ, |
||||||||
∂t |
|
|
∂t |
− |
4c2 |
|
|
|
r2 |
|||||||||||||||||
|
|
|
∂t |
|
|
|
|
|
|
|
rc |
|
|
|
|
|||||||||||
откуда после интегрирования по времени находим |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Er = 0, |
Eϑ = 0, |
|
|
|
|
|
|||||||
|
|
|
|
|
E |
|
= |
|
a2µ |
|
|
I00(t − r/c) |
+ |
I0(t − r/c) |
|
|
sin ϑ. |
(1.45) |
||||||||
|
|
|
|
|
|
− 4 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
ϕ |
|
|
|
rc |
|
|
|
|
|
r2 |
|
|
||||||||

14 1. ЭЛЕМЕНТАРНЫЕ ИЗЛУЧАТЕЛИ
Если ток в витке изменяется по гармоническому закону, то, как следует из (1.43) – (1.45), комплексные амплитуды ненулевых составляющих поля рамки будут определяться
выражениями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ik |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
H˙ r = |
|
I˙ |
|
+ |
|
|
|
|
e−ikr cos ϑ, |
|
|
|
|
(1.46) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
r3 |
r2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
1 |
|
|
|
|
|
ik |
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
H˙ ϑ = |
|
I˙ |
+ |
|
|
|
|
− |
|
|
|
e−ikr sin ϑ, |
|
|
(1.47) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
r3 |
r2 |
r |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
E˙ ϕ = |
a2 |
W0I˙ − |
ik |
+ |
k2 |
e−ikr sin ϑ. |
|
|
(1.48) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
r2 |
|
|
|
r |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
~ |
|
|
2 |
, выражения |
|||||||
Используя понятие магнитного момента витка M(t) = I(t)µS = ~ezI(t)µπa |
|||||||||||||||||||||||||||||||||||||||||||
для ненулевых компонент поля витка (1.43) - (1.45) можно переписать в виде |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
H |
|
|
= |
|
1 |
|
M0(t |
|
|
r/c) |
+ |
M(t − r/c) |
|
cos ϑ, |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2πµ |
|
|
|
r−2c |
|
|
|
|
|
|
|
(1.49) |
||||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
|
||||||||||||||||||||||
H |
|
= |
|
1 |
|
|
|
|
M00(t − r/c) |
|
+ |
M0(t − r/c) |
+ |
M(t − r/c) |
|
sin ϑ, |
(1.50) |
||||||||||||||||||||||||||
|
4πµ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
ϑ |
|
|
|
|
rc2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
r2c |
|
|
|
|
r3 |
|
|||||||||||||||||
|
|
|
|
E |
|
|
|
= |
|
1 |
|
|
M00(t − r/c) |
+ |
M0(t − r/c |
sin ϑ, |
|
|
(1.51) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
−4π |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
rc |
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|||||||||||||||||
где M(t) = I(t)µπa2 – величина магнитного момента.
Формально можно считать, что магнитный момент витка создан магнитным диполем – двумя точечными магнитными зарядами одинаковой величины и противоположного знака
+q |
м |
и −q |
м |
, расположенными на расстоянии ` |
~ |
м |
(t)` (положи- |
|
|
друг от друга: M(t) = ~ezq |
|
тельный магнитный заряд расположен выше отрицательного, как на рис. 1.1). Используя понятие магнитного тока, текущего между магнитными зарядами, M(t) = dqм/dt, из (1.49) - (1.51) получим следующее определение ненулевых компонент поля элементарного электрического витка через магнитные заряды и токи:
|
|
|
H |
|
= |
|
` |
|
M(t r/c) |
+ |
qм(t − r/c) |
|
|
cos ϑ, |
|
|
|
|||||||||
|
|
|
|
|
|
r−2c |
|
|
|
|
|
|
|
|
(1.52) |
|||||||||||
|
|
|
|
|
r |
|
2πµ |
|
|
|
r3 |
|
|
|
||||||||||||
H |
|
= |
` |
|
M0(t − r/c) |
+ |
M(t − r/c) |
+ |
qм(t − r/c) |
|
sin ϑ, |
(1.53) |
||||||||||||||
ϑ |
4πµ |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
rc2 |
|
|
|
|
r2c |
|
|
|
|
r3 |
|
|||||||||||
|
|
|
E |
|
|
= |
− |
` |
|
M0(t − r/c) |
+ |
M(t − r/c) |
sin ϑ. |
|
|
(1.54) |
||||||||||
|
|
|
|
|
4π |
|
|
|
|
|||||||||||||||||
|
|
|
|
ϕ |
|
|
rc |
|
|
|
r2 |
|
|
|
|
|||||||||||
Сравнение этих выражений с (1.29) – (1.31) показывает, что элементарный виток радиуса a с электрическим током I создаёт точно такое же электромагнитное поле, как и магнитный диполь Герца длиной ` с магнитным током
M = µπ a2 dI/dt.
`
При изменении тока по гармоническому закону комплексные амплитуды электричес-
˙ |
|
|
˙ |
кого тока в рамке I и магнитного тока эквивалентного магнитного диполя Герца M будут |
|||
связаны между собой соотношением |
|
|
|
˙ |
2π2a2 |
˙ |
(1.55) |
M = iW0 |
λ` |
I. |
|
Подставив это выражение в (1.36) и учитывая (1.38), найдём сопротивление излучения элементарного электрического витка:
|
π5 |
|
a |
|
4 |
|
RΣ = |
8 |
W0 |
|
. |
||
3 |
λ |
|||||

4. ЭЛЕМЕНТ ГЮЙГЕНСА |
15 |
В воздухе (вакууме)
RΣ = 320π6 a 4 Ом.
λ
4.Элемент Гюйгенса
Вряде практически важных случаев удобнее рассматривать элементарные излучатели не на физической поверхности или в объёме антенны, а на некоторой воображаемой поверхности, расположенной в окружающем антенну пространстве. Этот подход базируется на приведённой в начала п.2 эквивалентных поверхностных токов. Согласно этой теореме, при определении электромагнитного поля в пространстве не обязательно знать распределение источников поля в занимаемом ими объёме: достаточно знать распределение поля, создаваемого этими источниками на некоторой замкнутой поверхности, охватывающей источники поля. Обычно такую поверхность выбирают в зоне излучения источников возбуждения поля. При этом распределение поля на этой поверхности может быть определено приближенно, исходя из упрощённых моделей.
Итак, рассмотрим малый квадратный (со стороной `) участок такой поверхности, расположенной в зоне излучения электрических и магнитных токов, возбуждающих электромагнитное поле. Как было показано выше, поле, создаваемое элементарными токовыми излучателями, в зоне излучения имеет структуру плоской волны. Следовательно, поле, создаваемое возбуждающими токами, также можно локально считать полем плоской волны (как результат суперпозиции плоских волн, создаваемых элементарными излучателями, на которые можно разбить эти токи). Введём систему координат, как показано
|
|
|
|
|
|
|
Z |
6 |
|
|
|
W0 |
|
|
|
|
Z |
6 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
` |
|
|
|
|
|
I˙ t− |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
`/2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
- |
H~ τ0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˙ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
O |
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
` |
|
|
|
|
|
- |
|
|
M |
|
|
|
- |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Y |
|
|
|
|
|
|
|
Y |
|
|
|||||||||||||||||
|
|
|
|
|
- |
|
~ |
|
|
|
|
|
`/ |
|
|
|
|
|
`/ |
|
|
|
|
|
|
||||||
|
|
|
|
|
m~s |
|
j |
|
|
|
|
t |
2 |
|
|
|
|
t |
2 |
|
|
|
|
|
|||||||
|
|
0 |
|
|
W |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Eτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
t |
`/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
а) Эквивалентные поверхностные токи |
б) Эквивалентные диполи Герца |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
Рис. 1.5. К определению поля элемента Гюйгенса |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~˙ |
0 |
~˙ 0 |
, |
|
на рис. 1.5. Будем полагать, что токи, создающие исходное поле с векторами E |
|
|
и H |
||||||||||||||||||||||||||||
находятся внизу, под плоскостью XOY . Без потери общности можно считать, что касательные к рассматриваемой площадке составляющие векторов поля расположены так,
~˙ 0 |
˙ 0 |
~˙ 0 |
˙ 0 |
. Кроме того, амплитуды векторов |
как показано на рис. 1.5а: Eτ |
= ~exEτ |
и Hτ |
= ~eyHτ |
напряжённости электрического и магнитного полей связаны между собой соотношением
˙ 0 |
˙ 0 |
, |
(1.56) |
Eτ |
= W1Hτ |
где коэффициент W1 зависит от волнового сопротивления W среды под плоскостью XOY и от угла падения ϑп исходной волны на площадку. Если волна падает на площадку нормально (угол падения ϑп = 0◦), то W1 = W . Если ϑп 6= 0 и в плоскости падения4
4Плоскостью падения называется плоскость, проходящая через направление распространения волны и через нормаль к поверхности в точке падения
16 |
|
|
|
|
1. ЭЛЕМЕНТАРНЫЕ ИЗЛУЧАТЕЛИ |
|
||||
|
|
~ 0 |
|
˙ 0 |
˙ 0 |
˙ 0 |
˙ 0 |
˙ 0 |
/W . Соответственно, в этом случае, |
|
лежит вектор E |
, то Eτ |
= E |
cos ϑп и Hτ |
= H |
= E |
|||||
|
|
|
|
|
|
|
|
|
~ 0 |
, |
как видно из (1.56), W1 = W/ cos ϑп. Если же в плоскости падения расположен вектор H |
||||||||||
˙ 0 |
˙ 0 |
˙ 0 |
˙ 0 |
cos ϑп и W1 = W cos ϑп. Общий случай произвольной ориентации век- |
||||||
то Eτ |
= E |
, Hτ = H |
||||||||
торов поля относительно плоскости падения может быть представлен в виде суперпозиции рассмотренных вариантов.
Воспользовавшись (1.27) и (1.28) и учитывая, что вектор внешней нормали к площадке ~ns = ~ez, найдём плотность эквивалентных поверхностных электрических и магнитных
токов на площадке: |
|
|
|
1 |
|
|
~˙s |
= ~ex |
˙ 0 |
, |
|||
j |
|
Eτ |
||||
|
|
|
|
W1 |
|
|
|
˙ |
s |
|
˙ 0 |
|
|
m~ |
|
= ~eyEτ . |
|
|||
Если размер площадки мал, то комплексные амплитуды векторов напряжённости исходного поля и, соответственно, эквивалентных поверхностных токов одинаковы во всех точках площадки. В таком случае все эквивалентные электрические поверхностные токи можно заменить электрическим диполем Герца длиной ` с осью, ориентированной по оси
OX. Электрический ток в этом диполе равен |
|
|
|
˙ |
` |
˙ 0 |
(1.57) |
I = |
W1 |
Eτ . |
|
|
|
|
|
Аналогичным образом магнитные эквивалентные поверхностные токи заменим магнитным диполем Герца такой же длины, ориентированным вдоль оси OY с магнитным током
˙ |
˙ 0 |
(1.58) |
M = `Eτ . |
||
Таким образом, рассматриваемую площадку можно, как показано на рис. 1.5б, заменить двумя ортогональными диполями Герца: электрическим с током I˙, определяемым по (1.57), и магнитным с током M˙ , определяемым по (1.58).
Найдём поле, создаваемое этими диполями в произвольной точке P со сферическими координатами (r, ϑ, ϕ), расположенной в зоне излучения диполей. Можно показать, что
электрический диполь Герца создаст в точке P поле |
||||||||
˙ |
|
˙ 0 |
dS W0 |
|
|
|
||
|
E |
|
−ikr |
|
||||
~ I |
|
τ |
|
|
|
|
(−~eϑ cos ϑ cos ϕ + ~eϕ sin ϕ) , |
|
E |
= i |
|
|
|
e |
|
||
2λr W1 |
|
|||||||
где dS = `2 – площадь рассматриваемой площадки. Поле магнитного диполя в этой же
точке будет равно |
|
|
|
˙ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
˙ |
|
|
|
dS |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
E |
−ikr |
|
|
|
|
|
|
||||||||
|
|
~ M |
= −i |
τ |
|
|
|
(~eϑ cos ϕ − ~eϕ cos ϑ sin ϕ) . |
|
|
|||||||||
|
|
E |
2λr |
e |
|
|
|
|
|
||||||||||
Полное поле такой системы диполей |
|
|
|
|
|
|
|
|
|
||||||||||
E~˙ |
|
˙ 0 |
e−ikr ~eϑ cos ϕ |
1 + W1 |
cos ϑ − ~eϕ sin ϕ W1 |
+ cos ϑ . |
(1.59) |
||||||||||||
= E~˙ I + E~˙ M = −i 2τλr |
|||||||||||||||||||
|
|
E dS |
|
|
|
|
|
|
|
|
|
|
|
|
W0 |
|
W0 |
|
|
|
Если W1 = W0, то выражение для полного поля несколько упростится: |
|
|||||||||||||||||
|
|
˙ |
|
˙ 0 |
dS |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
E |
|
−ikr |
|
|
|
|
|
|
|
|
||||||
|
~ |
|
τ |
|
|
|
|
|
|
|
|
|
|
|
(1.60) |
||||
|
E = −i |
|
|
e |
|
|
|
(1 + cos ϑ) (~eϑ cos ϕ − ~eϕ sin ϕ). |
|
||||||||||
|
2λr |
|
|
|
|
||||||||||||||
Рассмотренная плоская площадка, имеющая малые в сравнении с длиной волны размеры, на поверхности которой одновременно присутствуют касательные компоненты E˙ τ0 и H˙ τ0, называется элементом Гюйгенса. Обычно поверхность, на которой ищутся эквивалентные токи, выбирается совпадающей с фазовым фронтом (поверхностью равных фаз) исходной волны, или волновой поверхностью (волновым фронтом). Соответственно, элемент Гюйгенса иногда называют элементом волновой поверхности (элементом

5. ЗАКЛЮЧЕНИЕ |
17 |
волнового фронта). Другими словами, элемент Гюйгенса – это участок волнового фронта плоской электромагнитной волны, размеры которого малы по сравнению с длиной волны.
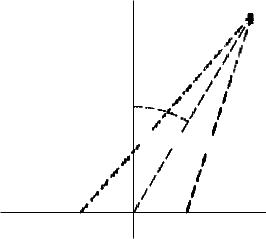
Как видно из (1.60), зависимость амплитуды поля от направления при W1 = W0 определяется выражением 1 + cos ϑ. График этой зависимости показан на рис. 1.6 (сплошная линия). Максимум излучения соответствует положительному направлению вектора Умова-Пойнтинга на площадке, т.е. направлению распространения исходной волны (при ϑ = 0). В противоположном направлении (ϑ = 180◦) поле минимально, и при W1 = W0
|
~˙ |
I |
направлен одинаково как при |
ϑ = 0, |
равно нулю. Это объясняется тем, что вектор E |
|
|||
˙ |
|
|
˙ |
|
так и при ϑ = 180◦, а вектор E~ M при |
ϑ = 0 совпадает по направлению с E~ I , а при |
|||
ϑ = 180◦ изменяет направление на обратное. Таким образом, при ϑ = 0 поля обоих диполей складываются, а при ϑ = 180◦ – вычитаются. Элемент Гюйгенса обладает большей направленностью излучения по сравнению с диполем Герца. Зависимость амплитуды поля от направления для диполя Герца показана на рис. 1.6 пунктирной линией.
Z 6

 -
-
X
Рис. 1.6. Характеристики направленности элемента Гюйгенса и диполя Герца
5.Заключение
Вэтой главе были рассмотрены свойства различных элементарных излучателей, расположенных в однородном пространстве. Поля, создаваемые ими в зоне излучения, имеют ряд общих свойств, а именно:
•Электромагнитная волна распространяется по прямой от источника поля;
|
|
|
|
|
~ |
~ |
|
• Векторы напряжённостей электрического E и магнитного H полей и единичный |
|||||||
|
|
|
|
|
|
|
~ |
|
вектор направления распространения волны p ортогональны между собой и обра- |
||||||
|
зуют правую тройку: |
|
|
|
|
|
|
|
~ |
~ |
|
1 |
|
|
~p; |
|
E × H = |
E~ |
H~ |
|
|
||
• |
~ ~ |
|
|
|
|
|
|
Ориентация векторов E и H в пространстве однозначно определяется расположе- |
|||||||
нием точки наблюдения относительно элементарного излучателя;
•Величины векторов напряжённостей электрического и магнитного полей связаны между собой соотношением
E~˙ |
|
= W0 |
H~˙ |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
где коэффициент W0 зависит только от параметров среды распространения;
18 |
1. ЭЛЕМЕНТАРНЫЕ ИЗЛУЧАТЕЛИ |
•Зависимость комплексных амплитуд векторов напряжённостей поля от расстояния r от излучателя до точки наблюдения определяется выражением e−ikr/r, где k – волновое число;
•Любой элементарный излучатель обладает определённой пространственной избирательностью (т.е. при фиксированном расстоянии до точки наблюдения величина создаваемого поля зависит от ориентации излучателя относительно точки наблюдения).
Иными словами, комплексные амплитуды векторов напряжённости электрического и магнитного полей электромагнитной волны, создаваемой элементарным излучателем в зоне излучения на расстоянии r в произвольной точке наблюдения P со сферическими координатами ϑ, ϕ, могут быть в общем виде представлены следующим образом:
|
|
˙ |
|
E |
|
|
|
e−ikr |
|
|||
|
|
~ |
|
|
|
˙ |
|
|
|
|
(1.61) |
|
|
|
E = ~e |
|
(ϑ, ϕ)KAf(ϑ, ϕ) |
|
r |
, |
|
||||
|
|
˙ |
H |
|
A˙ |
e−ikr |
|
|||||
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
H = ~e (ϑ, ϕ)K |
W0 |
f(ϑ, ϕ) |
r |
, |
|
|||||
где единичные векторы ~e |
E |
(ϑ, ϕ) и |
~e |
H |
|
|
|
~ |
~ |
|||
|
|
(ϑ, ϕ) показывают направления E и H в точке на- |
||||||||||
блюдения, коэффициент K зависит от типа излучателя и его размеров, A˙ – комплексная амплитуда тока возбуждения, функция f(ϑ, ϕ) описывает направленные свойства излучателя. При этом ~eE × ~eH = ~p, ~eH ×~p = ~eE, ~p × ~eE = ~eH .
Как видно из (1.61), поверхность равных фаз (фазовый фронт) для поля излучения элементарного излучателя является сферой с центром в точке, где расположен излучатель. Следовательно, элементарный излучатель в зоне излучения создаёт расходящуюся волну со сферическим фазовым фронтом или сферическую волну. Поверхность равных амплитуд (амплитудный фронт) будет задаваться уравнением r(ϑ, ϕ) = f(ϑ, ϕ). Учитывая, что элементарные излучатели обладают определённой пространственной избирательностью (т.е. f(ϑ, ϕ) не является константой), поверхности амплитудного и фазового фронтов не совпадают. Такие волны называются неоднородными.
При дальнейшем рассмотрении антенн будем по умолчанию полагать, что точка наблюдения расположена в зоне излучения для всех элементарных излучателей, на которые может быть разбита антенна, и, соответственно, опираться на эти свойства элементарных излучателей.
Глава 2
ХАРАКТЕРИСТИКИ АНТЕНН
1. Поле двух элементарных излучателей
Рассмотрим поле, создаваемое системой из двух одинаковых элементарных излучателей, расположенных на расстоянии d друг от друга, как показано на рис. 2.1.
Z 6 |
|
|
q P |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϑ |
|
|
|
r1 |
r0 |
|
r2 |
1 |
2 O q |
d/r |
2 |
- |
−d/r |
2 |
X |
Рис. 2.1. К определению поля системы из двух излучателей
Введём систему координат так, как показано на рис. 2.1. При этом проведём плоскость XOZ через оба излучателя и точку наблюдения P , совместив начало системы координат с центром отрезка между излучателями. Обозначим через r0 расстояние от начала системы координат до точки P , r1 и r2 – расстояния до точки наблюдения соответственно от первого и от второго излучателей.
Как следует из (1.61), поле в точке P будет определяться выражением
˙ |
E |
|
|
|
e−ikr1 |
E |
|
|
e−ikr2 |
|||
~ |
|
|
˙ |
|
|
|
|
˙ |
|
|
|
|
E = ~e1 |
(ϑ, ϕ)K1A1f1 |
(ϑ, ϕ) |
r1 |
+ ~e2 (ϑ, ϕ)K2A2f2 |
(ϑ, ϕ) |
|
, |
|
||||
где |
|
|
|
|
|
|
|
r2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r1(ϑ) = p |
|
, |
r2(ϑ) = p |
|
. |
|||||||
r02 + r0d sin ϑ + d2/4 |
r02 − r0d sin ϑ + d2/4 |
|||||||||||
Для простоты будем считать, что оба излучателя изотропны (т.е. абсолютно ненаправлены), в любой точке пространства создают одинаково направленные векторы поля и возбуждаются с одинаковыми амплитудами, т.е A˙1 = A˙2 = A˙. Тогда при перемещении точки наблюдения P в плоскости рисунка по окружности радиуса r0 вокруг точки O изменение поля системы излучателей (т.е. зависимость напряжённости поля от угла ϑ) будет определяться выражением
f(ϑ) = |
e−ikr1(ϑ) |
+ |
e−ikr2(ϑ) |
. |
|
|
|||
|
r1(ϑ) |
|
r2(ϑ) |
|
Это выражение удобнее переписать в виде
f(ϑ) = e−ikr1(ϑ) |
r1 |
(ϑ) + |
|
− |
r2(ϑ) |
|
. |
||
|
|
|
1 |
|
e |
|
ik[r2(ϑ)−r1 |
(ϑ)] |
|
19
20 2. ХАРАКТЕРИСТИКИ АНТЕНН
Нас будет интересовать зависимость от ϑ амплитуды создаваемого поля, т.е. функция
f0(ϑ) = |f(ϑ)| = |
r1 |
(ϑ) + |
e |
− |
r2(ϑ) |
|
|
, |
(2.1) |
||
|
|
1 |
|
|
ik[r2(ϑ)−r1 |
(ϑ)] |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Видно, что поле, создаваемое этими двумя излучателями, зависит |
как от самих расстояний |
||||||||||
r1(ϑ) и r2(ϑ), входящих в знаменатели слагаемых правой части выражения (2.1) (и определяющих амплитуды полей излучателей), так и от разности этих расстояний, входящей в показатель экспоненты в числителе второго слагаемого, т.е. от разности фаз полей излучателей.
Для сравнения степени влияния изменения амплитуд и фаз полей излучателей на величину поля рассмотрим следующие приближения функции f0(ϑ):
(1) рассматриваем только изменения знаменателей, пренебрегая разностью фаз и считая числитель второго слагаемого равным единице. При таком приближении вместо выражения (2.1) рассматривается функция
|
1 |
|
1 |
|
|
f1(ϑ) = |
|
|
+ |
|
. |
r1(ϑ) |
r2(ϑ) |
||||
Это приближение будем называть амплитудным (учитывается только изменение амплитуд полей излучателей с изменением расстояния);
(2) учитываем только изменение разности фаз, пренебрегая изменениями знаменателей, т.е. используем функцию
f2(ϑ) = 1 + e− |
r0 |
|
− |
r1 |
. |
|
|
|
ik[r2 |
(ϑ) |
|
(ϑ)] |
|
|
|
|
|
|
|
|
Это будем называть фазовым приближением.
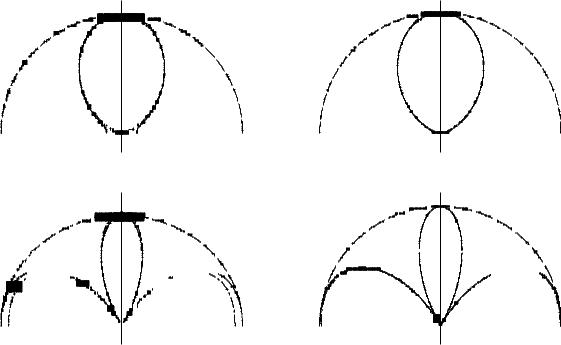
На рис. 2.2 представлены зависимости f0(ϑ) (сплошная линия), f1(ϑ) (пунктирная линия) и f2(ϑ) (штрих-пунктирная линия), рассчитанные при различных значениях d и r0. Как видно из представленных графиков, даже при малых расстояниях до точки наблю-
Z 6 |
Z 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) d = 0,5λ, r0 = 2λ |
|
|
|
|
|
|
|
|
|
а) d = 0,5λ, r0 = 5λ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
в) d = λ, r0 = 2λ |
|
|
|
г) d = λ, r0 = 5λ |
|||||||||||||||
Рис. 2.2. Различные приближения для поля системы из двух излучателей
дения (r0 = 2λ на рис. 2.2а и 2.2в) фазовое приближение даёт хорошее согласование с

2. ДАЛЬНЯЯ И БЛИЖНЯЯ ЗОНЫ АНТЕННЫ |
21 |
точным выражением (2.1) по сравнению с амплитудным. С ростом расстояния r0 влияние изменения r в знаменателе быстро убывает. Так, при r0 = 5λ (рис. 2.2б и 2.2г) распределение поля, задаваемое фазовым приближением, практически совпадает с точным. Таким образом, если расстояние от центра системы излучателей до точки наблюдения в несколько раз превышает линейный размер системы, изменением r в знаменателе выражения для поля излучателя можно пренебречь.
Действительно, если d < r0, то, разложив функции r1(ϑ) и r2(ϑ) в ряд Тейлора в окрестности точки d = 0 по степеням величины d/r0 и ограничившись первыми двумя членами разложения, можем записать
r1(ϑ) ≈ r0 |
1 + 2r0 |
sin ϑ , |
r2(ϑ) ≈ r0 |
1 − 2r0 |
sin ϑ . |
||
|
|
d |
|
|
|
d |
|
Так как амплитуда поля первого излучателя обратно пропорциональна расстоянию r1, а поле второго излучателя обратно пропорционально расстоянию r2, отношение амплитуд полей первого и второго излучателей будет равно отношению r2 к r1. С учётом последних приближенных выражений для r1 и r2 найдём:
|
|
|
1 − |
d |
sin ϑ |
|
|
|
r2 |
(ϑ) |
|
2r0 |
d |
|
|||
|
|
≈ |
|
|
|
≈ 1 − |
|
sin ϑ. |
r1 |
(ϑ) |
1 + |
d |
sin ϑ |
r0 |
|||
|
|
|
2r0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
Таким образом, при изменении ϑ отношение амплитуд полей излучателей в точке наблюдения будет меняться тем меньше, чем меньше отношение расстояния между излучателями
красстоянию до точки наблюдения.
Вто же время, как видно из рис. 2.2, пренебрежение изменением разности фаз полей излучателей приводит к кардинальному искажению распределения поля.
Распределение интенсивности излучаемого поля в пространстве определяется, прежде всего, фазовыми соотношениями полей, приходящих от элементарных излучателей, на которые можно разбить реальную антенну. Поэтому величина погрешности, допустимой при определении расстояний (вернее, разности расстояний) от различных элементов антенны до точки наблюдения должна быть мала по сравнению с длиной волны.
2. Дальняя и ближняя зоны антенны
Рассмотрим систему из N изотропных излучателей, показанную на рис. 2.3. Пусть
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
>* |
|
P |
|
|
|
|
|
|
|
~rn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bn |
|
|
|
|
|||||
BN |
~r |
|
|
|
||||||
soS |
|
|
|
|
|
|
|
|
|
|
|
s6 |
|
|
|
|
|
||||
%~NS |
|
q |
%~n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
B |
|
|
|
|||
|
S: |
|
|
|
|
|||||
|
O %~1s |
|
1 |
|
|
|
||||
B2 s %~2 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.3. К определению дальней зоны антенны
m-й излучатель расположен в точке Bm, m = 1, 2 . . . N. Введем сферическую систему координат и связанную с ней декартову. Начало системы координат расположим в точке O,

22 |
2. ХАРАКТЕРИСТИКИ АНТЕНН |
расположенной в области, занимаемой системой излучателей (в частности, точка O может совпадать и с одним из излучателей). Поле излучателей будем искать в точке наблюдения P , заданной сферическими координатами (r, ϑ, ϕ).
Обозначим радиус-вектор точки Bn через %~n. Очевидно, что
|
|
|
|
~ |
|
|
(2.2) |
|
|
%~n = xn~ex + yn~ey + zn~ez = ρnrn, |
|||||
где xn, yn и zn – декартовы координаты этой точки, ρn = |
|
|
– расстояние |
||||
|
xn2 + yn2 + zn2 |
||||||
от начала координат до |
n |
-го излучателя, |
~ |
– единичный |
вектор направления из начала |
||
rn |
|||||||
|
|
p |
|
||||
координат на эту точку. Вектор, соединяющий точку Bn с точкой наблюдения P , обозначим ~rn. Используя единичный вектор направления волны от n-го излучателя к точке наблюдения ~pn можем записать
~rn = rn~pn,
где rn – расстояние от n-го излучателя до точки наблюдения. Радиус-вектор точки наблюдения обозначим как ~r. Понятно, что
~r = r~er,
где r – расстояние от начала системы координат до точки наблюдения P . Найдём величину rn. Из рис. 2.3 видно, что ~rn = ~r − %~n. Отсюда получаем:
p p p
rn = ~rn · ~rn = (~r − %~n) · (~r − %~n) = r2 − 2rρn~er ·~rn + ρn2.
Полагая, что ρn r0, разложим последнее выражение в ряд Тейлора по степеням ρn/r и воспользуемся первыми тремя членами этого разложения:
|
|
|
|
|
|
|
|
|
~ |
2 |
2 |
|
|
|
r |
n ≈ |
r |
− |
~e |
r · |
%~ |
|
+ |
1 − (~er · rn) |
|
|
ρn |
. |
(2.3) |
n |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
r |
|||||||
Второе слагаемое в этом выражении зависит только от координат m-го излучателя и от направления на точку наблюдения. Третье слагаемое, кроме того, зависит и от расстояния r. Первое слагаемое равно расстоянию от начала координат до точки наблюдения и одинаково для всех излучателей системы.
Будем полагать, что при определении фазы поля, создаваемого излучателем, допустима ошибка δϕ. Определим, при каком расстоянии r абсолютная величина ошибки при отбрасывании в (2.3) третьего слагаемого не превысит этой допустимой величины, т.е. будет выполняться неравенство
~ |
2 |
ρn |
2 |
|
|
|
||
k |
1 − (~er · rn) |
|
|
≤ |
δφ. |
(2.4) |
||
|
|
|
r |
|
||||
2 |
|
|
|
|
||||
Выберем излучатели m и n так, чтобы расстояние между ними L = |%~m − %~n| было максимальным из всех расстояний между любыми двумя излучателями системы, т.е.
|%~m − %~n| ≥ |%~i − %~j|, i, j = 1, 2 . . . N.
В этом случае L является максимальным линейным размером системы излучателей (антенны). Положим %~m = 0, т.е. совместим начало системы координат O с точкой Bm. В этом случае неравенство (2.4) примет вид
k 1 − (~er ·~rn)2 L2 ≤ δφ.
2 r
Учитывая, что 1 − (~er ·~rn)2 ≤ 1 и k = 2π/λ, из последнего неравенства найдём:
r ≥ π L2 . δϕ λ
