13.Ачх и фчх в описании эц
ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Комплексная передаточная функция цепи:
К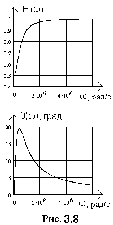
омплексная
передаточная функция
цепи не зависит от входного воздействия,
а определяется только структурой цепи
и параметрами её элементов. Для простоты
вычислений допустим, что на вход цепи
подаётся гармонический сигнал,
определяемый значением комплексной
амплитуды:
.
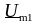Тогда комплексное амплитудное значение
тока в контуре будет равно:
,
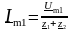а комплексное амплитудное значение
напряжения на выходе цепи:
.
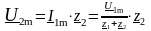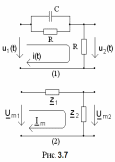
Для схемы на рисунке 3.7(1)
,
.
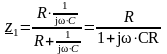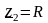Комплексная передаточная функция цепи:
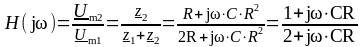
Эта функция может быть представлена в показательной форме:
.
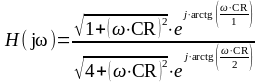Амплитудно-частотная характеристика (АЧХ) – это зависимость модуля комплексной функции от частоты. АЧХ передаточной функции по напряжению:
.
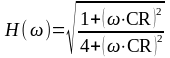Фазочастотная характеристика (ФЧХ) – это зависимость аргумента комплексной функции от частоты. ФЧХ передаточной функции по напряжению:
.
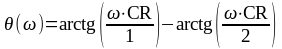Графики АЧХ и ФЧХ показаны на рисунке 3.8.
14.Резонансные явления в эц. Основные виды резонансов в эц
На всякий
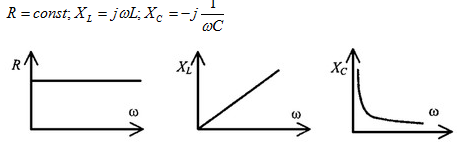
Резонанс в электрической цепи – это резкое возрастание амплитуды внутренних колебаний системы за счет совпадения частоты внутренних колебаний с частотой внешнего воздействия.
Резонансом в
электрических цепях называется режим
участка электрической цепи, содержащей
индуктивный и емкостной элементы, при
котором разность фаз между напряжением
и током равна нулю 
.
Режим резонанса может быть получен при
изменении частоты 
питающего
напряжения или изменением параметров
элементов L и С.
При
последовательном соединении возникает
резонанс напряжения.
Последовательное
соединение R,
L, C.
Резонанс токов через реактивные элементы
Резонанс токов возникает при параллельном соединении реактивных сопротивлений с одинаковыми характеристиками в цепях с переменным током. Во время резонанса токов реактивная индуктивная проводимость приравнивается к реактивной емкостной проводимости.
Колебания контура с определенной частотой совпадают с частотой колебаний источника.
Простейшим примером цепи, в которой может произойти резонанс токов, есть параллельное соединение катушки с конденсатором.
Для обеспечения резонанса силы тока или напряжения в цепи необходима ее проверка с целью определения суммарного сопротивления и проводимости. Кроме того, ее мнимая часть должна равняться нулю.
Резонанс напряжений
Резонанс напряжений имеет место в цепи переменного тока в случае последовательного соединения активного RR, емкостного CC и индуктивного LL компонентов. Резонанс напряжений состоит в совпадении внутренних колебаний источника и внешних колебаний контура. Резонанс напряжений применяется с пользой, но бывает и опасен. Например, данное явление применяют в радиотехнике, а опасность его состоит в том, что при резких скачках напряжения может произойти поломка оборудования и даже его возгорание.
Резонанс напряжения достигают несколькими путями:
подбирая индуктивность катушки;
подбирая емкость конденсатора;
подбирая угловую частоту ω0ω0.
Эти величины подбирают с помощью таких формул:
L0=1/ω2CL0=1/ω2C
C0=1/ω2L
Частота ω0 – это резонансная величина. При постоянных напряжении и активном сопротивлении в цепи сила тока в процессе резонанса напряжения наибольшая и равняется отношению напряжения к активному сопротивлению. То есть, сила тока полностью не зависима от реактивного сопротивления. Если реактивные сопротивления индукции и емкости одинаковы и по своей величине превышают активное сопротивление, тогда на зажимах катушки и конденсатора будет напряжение, сильно превышающее напряжение на зажимах контура.
Величина Q является добротностью контура и описывает его резонансные характеристики. Q=UC0/U