2.1.2. Параметры гармонических колебаний

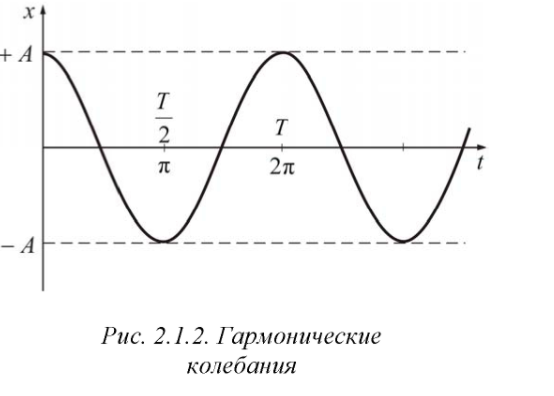
К параметрам гармонических колебаний относятся: смещение, амплитуда, фаза колебаний и т. д.

• Расстояние груза от положения равновесия до точки, в которой находится груз, называют смещением x.

• Максимальное смещение - наибольшее расстояние от положения равновесия - называется амплитудой и обозначается буквой A.

• Выражение, стоящее под знаком синуса или косинуса в формуле (1.1.2), ω t + φ определяет смещение x в данный момент времени t и называется фазой колебания.

• Величина φ называется начальной фазой колебания и определяет смещение в начальный момент времени (t = 0). Фаза измеряется в радианах и определяет значение колеблющейся величины в данный момент времени.

Так как синус и косинус изменяются в пределах от +1 до -1, то х может принимать значения от +А до -А (рис. 2.1.2).

• Движение от некоторой начальной точки до возвращения в ту же точку, например от x = A к x = -A и обратно в x = A, называется полным колебанием. Частота колебаний ν определяется как число полных колебаний в 1 секунду. Частоту, как правило, измеряют в герцах (Гц): 1 Гц равен одному полному колебанию в секунду. Очевидно, что ν = 1/T. (2.1.2)

• Т - период колебаний - минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание

• ω₀ - циклическая (круговая) частота - число полных колебаний за 2π секунд:

ω₀ = 2πν. (2.1.4)

Частота и период гармонических колебаний не зависят от амплитуды. Изменяя амплитуду колебаний груза на пружине, мы не изменяем частоту колебаний этой системы.

Колебания характеризуются не только смещением, но и скоростью v_x, и ускорением a_x. Если смещение описывается уравнением x = A cos(ω₀t + φ), то, по определению, ...

В этих уравнениях v_m =ω₀A - амплитуда скорости; a_m =ω₀²A - амплитуда ускорения.

Из уравнений (2.1.5) и (2.1.6) видно, что скорость и ускорение также являются гармоническими колебаниями.

8.Метод комплексных амплитуд в тэц. Область его применения.

Основой для создания метода комплексных амплитуд служат свойства гармонических колебаний: при алгебраическом суммировании (сложении или вычитании), дифференцировании и интегрировании гармонических колебаний с одинаковыми частотами их форма сохраняется, изменяются лишь амплитуда и начальная фаза результирующего колебания. Указанные свойства гармонических колебаний позволяют свести описание цепи в виде интегро-дифферен- циальных уравнений к уравнениям, для решения которых используется алгебра комплексных чисел. При гармоническом воздействии задача анализа установившегося режима состоит в определении комплексной амплитуды, содержащей сведения об амплитуде и начальной фазе отклика (чем и обусловлено название метода).

В теории цепей метод комплексных амплитуд получил широкое распространение благодаря:

• • потребности проведения анализа при гармоническом воздействии, поскольку гармонические колебания используются для питания различных электротехнических устройств, для передачи информации, в качестве тестовых сигналов при наладке и испытаниях электронной аппаратуры и т.п.;

• • простоте проведения анализа и выполнения расчетов с использование рассмотренных выше методов для резистивных цепей постоянного тока;

• • возможности использования результатов анализа на воздействия произвольных периодических и непериодических сигналов (с помощью рядов Фурье и интеграла Фурье по принципу наложения).

//////////////////////////////////////Дальше про метод\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Обоснование и сущность метода. Для обоснования метода комплексных амплитуд воспользуемся интегро-диф- ференциальным уравнением параллельного колебательного контура (рис. 3.2.1, а)

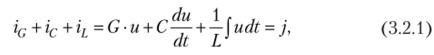
полагая, что на цепь воздействует ток

Решение уравнения (3.2.1) будем искать в виде

Необходимо определить амплитуду U и начальную фаз}' (p_t, напряжения.

Используя (3.1.2), представим ток (3.2.2) и напряжение (3.2.3) в комплексной форме:

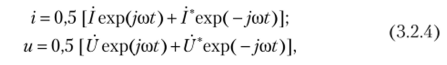
где

Подставив (3.2.4) в (3.2.1) и приравняв коэффициенты при ехр(/со?) и ехр(-усо?), получим систему из двух уравнений

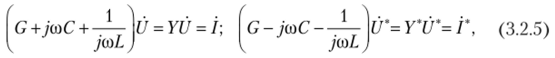
где У, У* представляют собой суммарную комплексную проводимость отдельных элементов цепи (см. рис. 3.2.1, а), что показано ниже.

Из (3.2.5) находим U= I/Y, U* = Г/У*, после чего определяем амплитуду U и начальную фазу напряжения (3.2.3). Оба уравнения (3.2.5) имеют одинаковые решения:

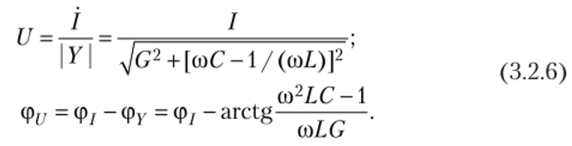
На основании (3.2.6) можно записать искомое напряжение в виде функции времени:

Как показал рассмотренный пример, сущность метода комплексных амплитуд состоит в замене интегро-дифферен- циального (или дифференциального) уравнения (3.2.1) уравнением в комплексной форме (3.2.5) и его решении относительно комплексной амплитуды напряжения. Поскольку оба уравнения (3.2.5) имеют одинаковые решения (3.2.6), достаточно составить только одно уравнение. Для составления уравнения можно использовать комплексное представление исходной схемы (рис. 3.2.1, б).

Анализ электрической цепи на рис. 3.2.1, б по методу комплексных амплитуд проводится в следующей последовательности:

• осуществляется переход от мгновенных значений напряжений и токов (3.2.2), (3.2.3) к их изображениям в комплексной форме:

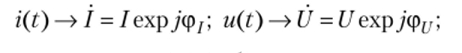
• • для схемы на рис. 3.2.1, б составляется уравнение равновесия (3.2.5);

• • уравнение (3.2.5) решается относительно комплексной амплитуды U, после чего определяются амплитуда U и начальная фаза cp_t/ напряжения;

• • осуществляется обратный переход от изображения U к мгновенному значению (3.2.7).

Рис. 3.2.1. Схема параллельного колебательного контура (а) и ее комплексное представление (б)

Теперь перейдем к непосредственному изложению метода комплексных амплитуд.

Комплексная форма описания цепей. Пассивные двухполюсники. Рассмотрим двухполюсную цепь с гармоническими напряжением и током:

и представим их в виде комплексных величин

Если одну из величин принять в качестве воздействия, а другую — в качестве отклика, то можно получить два вида передаточных функций, одна из которых имеет размерность сопротивления, другая — проводимости:

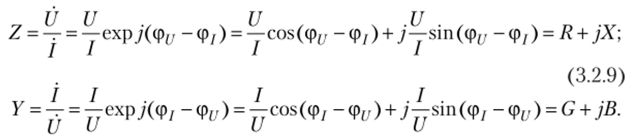
Эти функции могут служить в качестве характеристик пассивных двухполюсных цепей. Отметим, что аналогичная ситуация имеет место и в резистивных цепях, единственный пассивный элемент которых также характеризуется сопротивлением R = u/i = U/I или проводимостью G = i/u = I/U.

Поскольку для резистивных двухполюсников ф₆г = ср₇, из (3.2.9) получаем 

Введение понятий комплексного сопротивления Z и проводимости Y позволяет описать (характеризовать) емкостные и индуктивные двухполюсники.

Емкостные двухполюсники. Пусть на емкость воздействует гармоническое напряжение. В этом случае на основании общей взаимосвязи между напряжением на емкости и протекающим током получаем выражение для комплексной амплитуды тока:

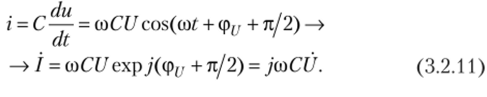
Аналогично при воздействии на емкость гармонического тока получим выражение для комплексной амплитуды напряжения:

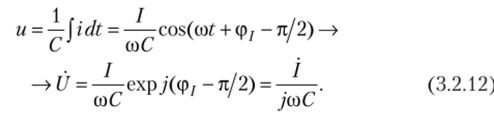
Используя выражения (3.2.11), (3.2.12), определяем соответственно комплексную проводимость и комплексное сопротивление идеальной емкости:

Индуктивные двухполюсники. На основании принципа дуальности запишем выражения для комплексных сопротивления и проводимости идеального индуктивного двухполюсника:

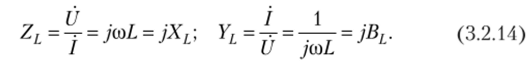
Вещественную и мнимую части в выражениях (3.2.9) называют активной и реактивной составляющими комплексного сопротивления и проводимости. Поэтому в теории цепей резистивные двухполюсники (3.2.10) относят к активным элементам, а емкостные (3.2.13) и индуктивные (3.2.14) — к реактивным.

Н с з а в и с и м ы е источники. С помощью источников напряжения и тока задают воздействующие на цепь колебания. Для их описания используют выражения (3.2.8).

Уравнения равновесия. При анализе цепей комплексным методом (так же, как и резистивных) составляют топологические и компонентные уравнения. Для топологического описания используются законы Кирхгофа в комплексной форме, согласно которым сумма комплексных амплитуд токов в узле и амплитуд напряжений в контуре должна быть равна нулю:

Для описания компонентов используются соотношения (3.2.10), (3.2.13), (3.2.15).

Особенности анализа. Прежде всего отметим, что при использовании комплексных величин и законов Кирхгофа в комплексной форме для описания цепей отсутствует необходимость в предварительном составлении систем дифференциальных уравнений и последующем их преобразовании в алгебраические уравнения для комплексных амплитуд.

Исходными данными при анализе служит комплексная схема замещения динамической цепи, содержащая базисные элементы R, G, L, С, U> I. По схеме замещения составляются уравнения равновесия для комплексных амплитуд аналогично резистивным цепям. Для проведения анализа установившегося режима можно использовать все методы, рассмотренные в гл. 2 для резистивных цепей:

• • методы эквивалентного преобразования схем;

• • методы Кирхгофа, контурных токов и узловых напряжений;

• • методы наложения, взаимности, эквивалентного источника.

Поэтому анализ динамической цепи методом комплексных амплитуд отличается от анализа резистивных цепей лишь формальными признаками. Постоянными величинами во всех соотношениях и уравнениях являются комплексные сопротивления Z(/co) и проводимости У(/со), а переменными — комплексные амплитуды напряжения Г/(со) и тока /(со). Однако при анализе комплексным методом учитываются не только амплитуды и начальные фазы переменных, но и их зависимость от частоты со. Эта особенность цепей при гармоническом воздействии обусловлена тем, что сопротивления (или проводимости) индуктивных и емкостных элементов зависят от частоты. Для выявления всех свойств цепи в установившемся режиме необходимо исследовать ее основные показатели (функции, характеристики, параметры) при изменении частоты от 0 до оо. Зависимость соответствующего показателя цепи от частоты называют частотной характеристикой. Поскольку параметры (сопротивления и проводимости) комплексной схемы замещения цепи и комплексные амплитуды напряжений и токов зависят от частоты (а не от времени), анализ по методу комплексных амплитуд относят к методам анализа в частотной области.

Следует отметить еще одну характерную особенность анализа цепей комплексным методом, которая рассмотрена ниже и состоит в возможности использования векторных диаграмм для наглядного представления фазовых соотношений токов и напряжений в анализируемой цепи.

Показатели электрических цепей. Свойство линейных цепей сохранять форму отклика при гармоническом воздействии позволяет обоснованно подойти к выбору их показателей и характеристик. При прохождении через линейную цепь входное колебание aj = ^!cos(co? + изменяет лишь амплитуду и начальную фазу, в результате чего отклик принимает вид а₂ = A₂cos((ot + Ф₂). Поэтому в качестве показателя можно принять отношение отклика к воздействию в комплексной форме, который будем назвать комплексной функцией цепи. Она может иметь различный физический смысл. Если отклик и воздействие фиксируются на одних и тех же полюсах (рис. 3.2.2, а), то комплексная функция цени отражает сопротивление (U — отклик, I — воздействие) или проводимость (I — отклик, 0 — воздействие) двухполюсника. Если же отклик фиксируется на одних полюсах, а воздействие — на других, то их отношение представляет собой передаточную функцию К (рис. 3.2.2, б). В зависимости от того, какие пары из четырех величин U_{, /), U₂> 1₂ используются в качестве отклика и воздействия, передаточная функция может быть безразмерной (U₂, U_x или /₂, /j), иметь размерность сопротивления (U_v /₂) или проводимости (/₂, U_{).

Так как в электрическую цепь входят реактивные двухполюсники, комплексные сопротивления и проводимости которых зависят от частоты воздействия, то комплексную функцию цепи можно представить в следующем виде:

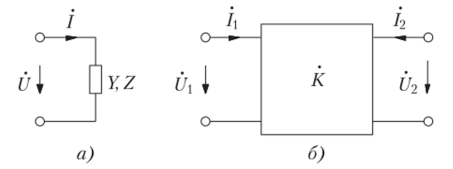
Рис. 3.2.2. Комплексная функция двухполюсника (а) и четырехполюсника (б)

где |Я(/со)|, arg H(ja> — модуль и аргумент комплексной функции Я(/со), причем

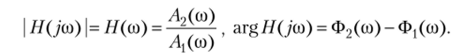
Отношение отклика к воздействию (3.3.16) называют комплексной частотной характеристикой, а зависимости модуля |Я(/со)| и аргумента argH(jw) от частоты со гармонических колебаний — амплитудно-частотной характеристикой (АЧХ) и фазо-частотной характеристикой (ФЧХ) соответственно. Обычно при определении АЧХ и ФЧХ принимают Aj=const, Oj=const.

https://studme.org/309881/tehnika/metod_kompleksnyh_amplitud