9.Описание эц в режиме постоянного тока и гармонического тока.

При постоянном токе ЭЦ находится постоянно под определённым напряжением, так же ток постоянен и не изменяется ни в величине, ни в направлении.

Переменные ток и напряжение характеризуются уже несколькими величинами. Чем сложнее их форма, тем больше величин характеризует соответствующие колебания.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

Гармоническими называют воздействия, мгновенные значения которых выражаются косинусными и синусными функциями. В более общем виде комплексными экспоненциальными функциями.

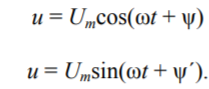
Гармоническое колебание является периодической функцией времени. На рис.1 отмечены амплитуда Um (максимальное значение) колебания и его период Т = 1/f, где f – частота колебания. Величина θ = ωt + ψ называется текущей фазой колебания и представляет собой некоторый угол, величина которого зависит от времени. Постоянная величина ψ называется начальной фазой, определяющей величину смещения гармонической функции относительно начала координат. Величина ω пропорциональна частоте f; она носит название угловой частоты и равна 2πf. Угловая частота является скоростью изменения текущей фазы, т. е.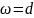 θ/dt , и измеряется в радианах в секунду (рад/с). .

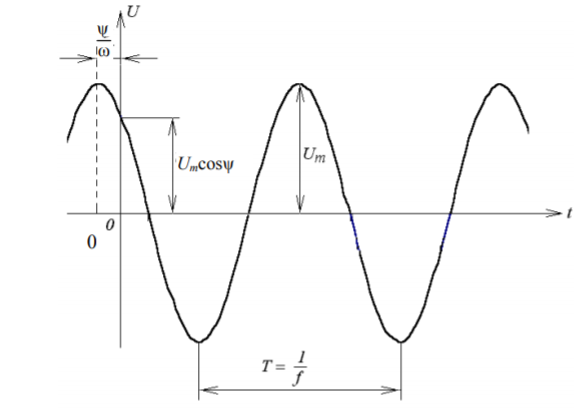
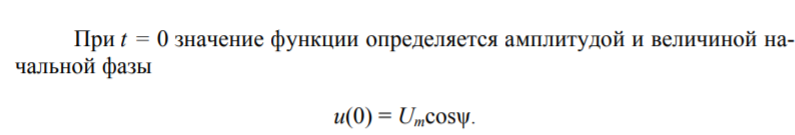
Среднее значение периодической функции за период Т определяется

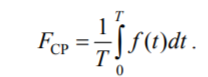
В случае гармонического колебания среднее значение за период равно высоте прямоугольника с основанием Т, площадь которого равна площади, ограниченной функцией f(t) и осью абсцисс и равна нулю, так как площадь положительной полуволны компенсируется площадью отрицательной полуволны. Поэтому под средним значением гармонической функции понимают среднее значение за полпериода. Для гармонического напряжения

При токе гармонической формы

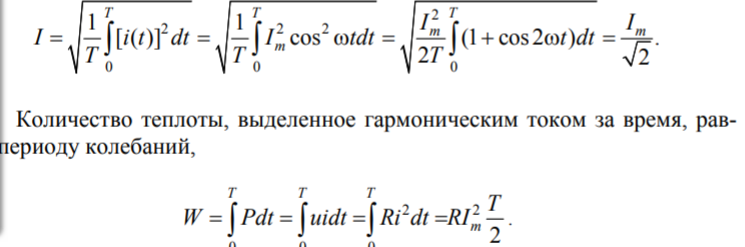
Представление гармонических функций с помощью комплексных величин. При гармоническом воздействии на линейную цепь все токи и напряжения имеют форму гармонических колебаний, поэтому задача расчета цепи сводится к нахождению амплитуд и начальных фаз этих колебаний. В связи с этим был разработан метод комплексных амплитуд, основанный на представлении гармонических функций в виде проекций вращающихся векторов, которые выражаются аналитически в комплексной форме. Метод удобно сочетает аналитические расчеты с геометрическими представлениями. Гармонические колебания согласно методу комплексных амплитуд могут быть представлены как проекции вектора Um на комплексной плоскости вращающегося против часовой стрелки с угловой частотой ω (рис. ) на оси координат

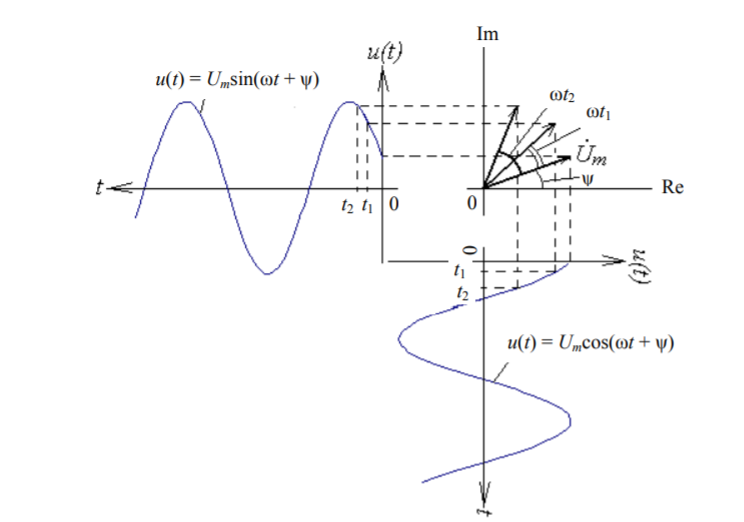
рис.

векторов.

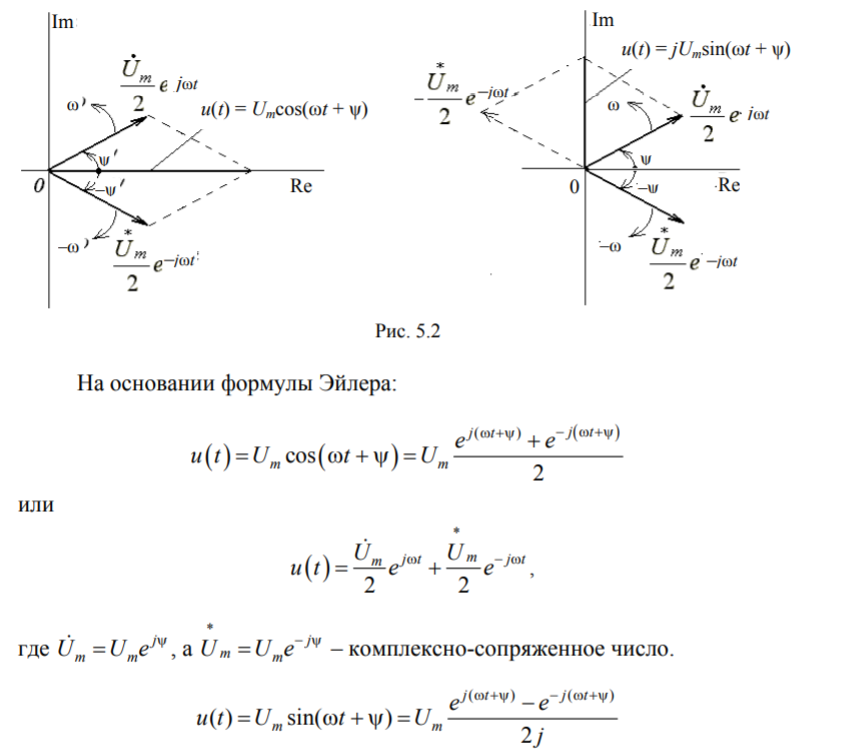
Вращение векторов в отрицательном направлении (по ходу часовой стрелки (рис. 5.2) связано с понятием отрицательной частоты, что, конечно, лишено физического смысла, однако позволяет упростить решение многих задач в радиотехнике и электронике. Таким образом, при рассмотрении напряжений и токов в цепи при гармоническом воздействии может быть построена векторная диаграмма, представляющая собой совокупность радиус-векторов, отображающих комплексные амплитуды колебаний и вращающихся на комплексной плоскости против часовой стрелки с угловой скоростью ω.

Поскольку взаимное расположение векторов на диаграмме не изменяется, то удобно рассматривать комплексные амплитуды напряжений и токов в момент времени t = 0.

На рис. 5.3 приведено схематическое изображение цепи переменного тока. Генератор гармонических колебаний питает пассивный двухполюсник П.

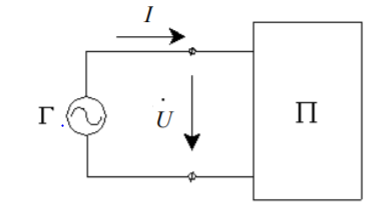
10.Понятие баланса мощности в ЭЦ при гармонической ЭДС

условие баланса мощности в цепях при гармоническом воздействии. В силу справедливости первого и второго законов Кирхгофа для комплексных действующих значений тока   и напряжения   в каждой из ветвей рассматриваемой цепи можно записать теорему Телледжена в комплексной форме

Однако поскольку ЗТК справедлив и по отношению к сопряженным токам   , то можно записать .Это уравнение отражает баланс комплексной мощности, согласно которому сумма комплексных мощностей, потребляемых всеми ветвями цепи, равна нулю. Баланс комплексной мощности можно сформулировать и в другой форме: сумма комплексных мощностей, отдаваемых независимыми источниками, равна сумме комплексных мощностей, потребляемых остальными ветвями электрической цепи:

 

Из условия баланса комплексной мощности следуют условия баланса активных и реактивных мощностей:

 ;