40.Определение дпф. Область применения дпф. Прямое и обратное дпф

 Преобразование Фурье является основоположником спектрального анализа. Спектральный анализ – это способ обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. В зависимости от того, каким образом представлен сигнал, используют разные преобразования Фурье. Подразумевается, что обрабатываемый сигнал имеет конечную длительность.

ДПФ широко применяется в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука, сжатии изображений), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале.

• Прямое дискретное преобразование Фурье ставит в соответствие временной функции  , которая определена N-точками измерений на заданном временном интервале, другую функцию  , которая определена на частотном интервале. Следует отметить, что функция на временном интервале задается с помощью N-отсчетов, а функция на частотном интервале задается с помощью K-кратного спектра.

N ˗ количество значений сигнала, измеренных за период, а также кратность частотного спектра;

k ˗ индекс частоты.

Частота k-го сигнала определяется по выражению

где T — период времени, в течение которого брались входные данные. 

• Обратное дискретное преобразование Фурье ставит в соответствие частотной функции  , которая определена K-кратным спектром на частотном интервале, другую функцию  , которая определена на временном интервале.

N ˗ количество значений сигнала, измеренных за период, а также кратность частотного спектра;

k ˗ индекс частоты.

Как уже было сказано, дискретное преобразование Фурье N-точкам дискретного сигнала   ставит в соответствие N-комплексных спектральных отсчетов сигнала  . Для вычисления одного спектрального отсчета требуется N операций комплексного умножения и сложения.

41.Основные свойства дпф. Операции циклической свёртки и циклического сдвига.

1. Линейность ДПФ. ДПФ суммы дискретных последовательностей длительности N равна сумме ДПФ слагаемых суммы и имеет длину N:

 

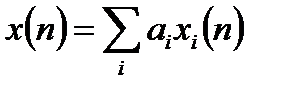 ; (2.1)

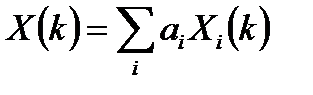 . (2.2)

 

2. ДПФ сумм последовательностей разной длины. Если в исходной сумме последовательностей   разные длины: N₁, N₂, N₃, …, то перед вычислением ДПФ всей последовательности необходимо привести последовательности к одинаковой длине N, равной максимальной длине исходных последовательностей, за счет дополнения нулями.

 

3. Сдвиг ДПФ. Сдвиг ДПФ по оси k вправо на величину k₀ соответствует умножению исходной последовательности на комплексную экспоненту   :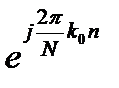

 

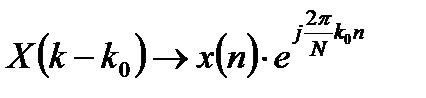 . (2.3)

4. Сдвиг исходной последовательности. Сдвиг последовательности вправо на m отсчетов (задержка последовательности) соответствует умножению ДПФ на комплексную экспоненту   :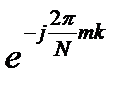

 

 . (2.4)

5. Теорема Парсеваля. Теорема Парсеваля для периодических и конечных последовательностей:

 

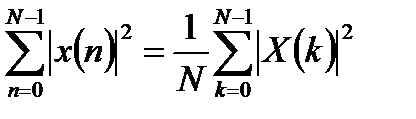 . (2.5)

Теорема Парсеваля утверждает, что энергию сигнала можно вычислить как по переменной n во временной области, так и по переменной k в частотной области.

Циклический временной сдвиг

Рассмотрим сигнал   как результат циклического временного сдвига исходного сигнала  , как это показано на рисунке 1 для положительных и отрицательных значений  .

Циклический сдвиг характерен периодическим сигналам. Спектр   сигнала   с циклическим временным сдвигом равен:

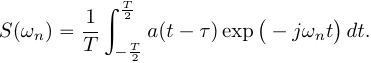
(3)

Введем замену переменной  , тогда  ,  , и выражение (3) преобразуется к виду:

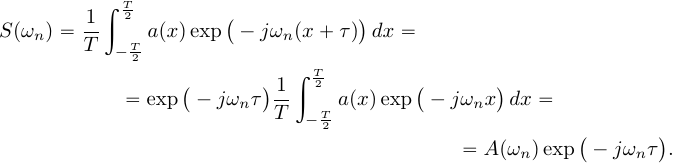
Циклическая свёртка пеиодических сигналов

Пусть сигнал   представляет собой циклическую (периодическую) свертку [2, стр. 362] сигналов   и 

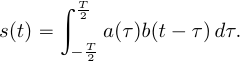
(5)

Тогда сигнал   также периодический с периодом   и его спектр равен:

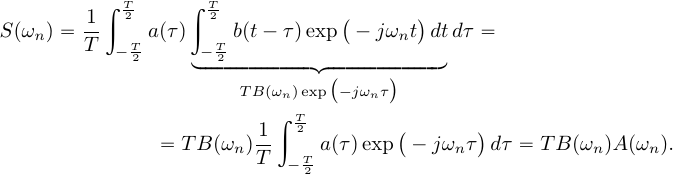
Спектр   периодического сигнала (5) пропорционален произведению спектров   и   сигналов   и  .

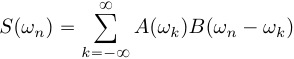
Частотный сдвиг периодического сигнала

Сигнал   представляет собой произведение сигналов   и комплексной экспоненты с частотой  , где   — произвольное целое число. Выбор частоты   обеспечивает периодичность сигнала  , поскольку на одном периоде   укладывается целое число оборотов комплексной экспоненты  .

Его спектр равен:

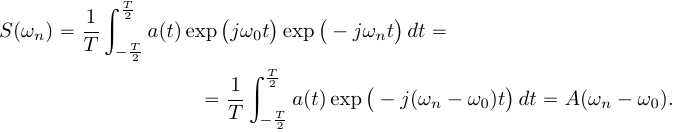
Умножение сигнала на комплексную экспоненту   переносит спектр сигнала на частоту  . При этом сигнал   становится комплексным, а его спектр — несимметричным относительно нулевой частоты.

Рассмотрим теперь умножение сигнала   не на комплексную экспоненту, а на гармоническое колебание  , где  ,   — произвольное целое число,   — произвольная начальная фаза. Выразим   через сумму комплексных экспонент , тогда:

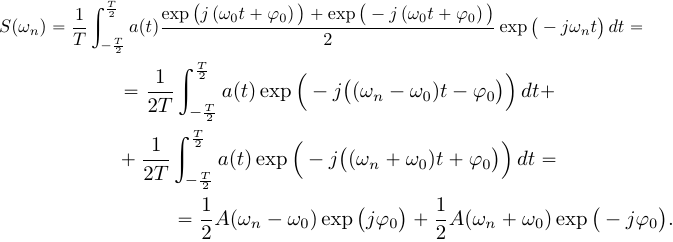
Таким образом, умножение сигнала на гармоническое колебание приводит к смещению спектра на частоты   как в положительную, так и в отрицательную области частот, уменьшению амплитуды в положительной и отрицательной областях в два раза и добавлению фазового множителя  .