- •1.Расчёт режима эц методом контурных токов.
- •2.Расчёт режима эц методом узловых потенциалов
- •3.Расчёт режима эц методом эквивалентного генератора
- •4.Расчёт режима эц методом наложения
- •5.Расчёт режима эц методом законов Кирхгофа
- •2.1.2. Параметры гармонических колебаний
- •8.Метод комплексных амплитуд в тэц. Область его применения.
- •9.Описание эц в режиме постоянного тока и гармонического тока.
- •11.Понятие баланса мощности в эц при негармонической периодической эдс
- •12.Понятие комплексного сопротивления эц
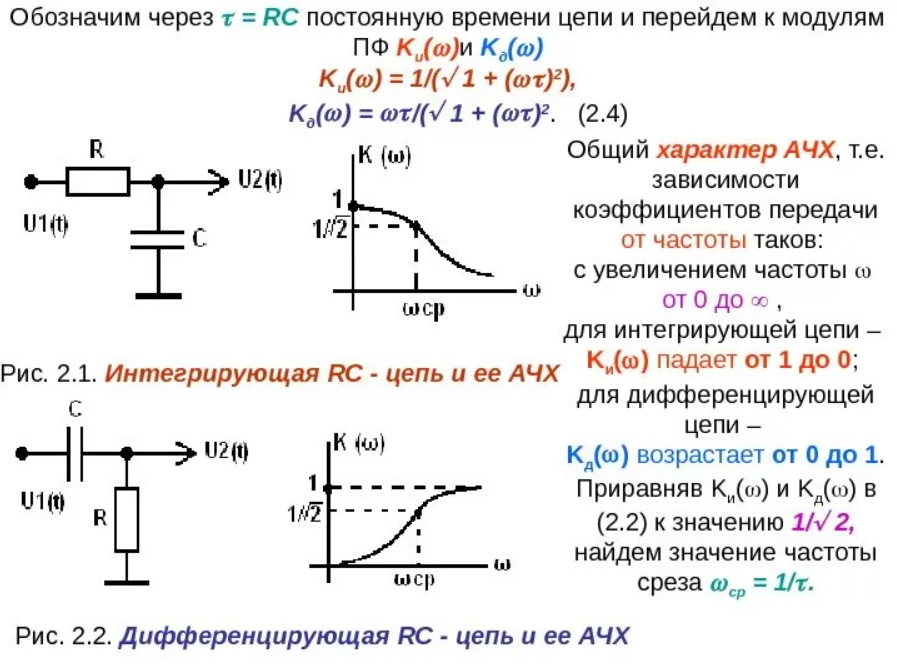
- •13.Ачх и фчх в описании эц
- •14.Резонансные явления в эц. Основные виды резонансов в эц
- •Резонанс напряжений
- •15.Схема и основные параметры последовательного колебательного контура
- •16.Схема и основные параметры параллельного колебательного контура
- •17.Анализ эц при негармоническом периодическом воздействии.
- •18.Применение рядов Фурье в анализе работы эц.
- •19.Форма представления ряда Фурье (одна из трёх по выбору)
- •Тригонометрическая форма
- •Вещественная форма
- •Комплексный (экспоненциальный) ряд Фурье
- •20.Спектры гармонического и негармонического колебаний. Графическая иллюстрация.
- •21.Классический метод решения при анализе переходных процессов в эц
- •22.Вынужденные и свободные составляющие переходных процессов
- •23.Виды начальных условий и законы коммутации.
- •24.Диффенцирующие и интегрирующие цепи. Частотные характеристики этих цепeй
- •25.Процедура и этапы расчёта эц операторным методом.
- •26.Методы определения оригинала тока или напряжения по известному изображению.
- •27.Единичная функция (включения) её связь с импульсной функцией. 1-14
- •28.Переходная характеристика и её связь с импульсным откликом 1-15
- •29.Определение параметра скважность импульсной последовательности. Влияние скважности на форму спектра.
- •30.Определение формы спектра производной периодического сигнала по известной форме спектра этого сигнала.
- •31.Интегральное преобразование Фурье. Его отличие от ряда Фурье с позиции тэц.
- •32.Прямое и обратное преобразование Фурье. Их связь с характеристиками эц.
- •33.Условие безыскажённой передачи сигнала по эц.
- •34. Теорема запаздывания в преобразовании Фурье и её применение в тэц.
- •35.Теорема о свёртке и её применение в тэц.
- •36.Физический смысл равенства Парсеваля и его применение
- •37.Дискретизация непрерывного сигнала. Теорема Котельникова.
- •38.Связь спектров непрерывного сигнала до и после дискретизации.
- •39.Условие безыскажённого восстановления непрерывного сигнала из дискретизированного.
- •40.Определение дпф. Область применения дпф. Прямое и обратное дпф
- •41.Основные свойства дпф. Операции циклической свёртки и циклического сдвига.
- •42.Эффект растекания дпф. Средства борьбы с растеканием.
- •43.Алгоритмы бпф их виды и роль в цифровой обработке сигналов.
- •44.Эффективность бпф и теоретические основы алгоритмов
- •45.Классификация основных видов частотно-избирательных фильтров. Частотные характеристики.
- •46.Рабочие параметры частотно-избирательных фильтров. Графическая иллюстрация этих параметров.
- •47.Нереализуемость идеальных фильтров на примере идеального фнч.
- •48.Дифференциальные уравнения и передаточные функции. Нули и полюса передаточной функции.
- •49.Условия физической реализуемости и устойчивости передаточной функции.
- •50.Полиномиальные фильтры. Основные типы: фильтры Баттерворта и Чебышева.
- •51.Процедуры синтеза полиномиальных фильтров. Определение порядка фильтра.
- •52.Нормированные и денормированные частотные характеристики фильтров прототипов. Переход от фнч прототипа к фвч фильтру. Нормирование параметров фильтра и преобразование частоты
- •Понятие фнч-прототипа
- •53.Активные rc фильтры. Преимущества и недостатки arc фильтров на примере схем с операционными усилителями.
- •54.Цепи с сосредоточенными и распределёнными параметрами. Первичные параметры длинных линий, их физический смысл.
- •55.Уравнение передачи однородной длинной линии. Падающие и отражённые волны.
- •56.Вторичные параметры длинных линий. Входное сопротивление длинной линии.
24.Диффенцирующие и интегрирующие цепи. Частотные характеристики этих цепeй
Дифференцирующие цепи — это цепи, на выходе которых напряжение пропорционально производной входного напряжения.
Дифференцирующую цепь можно представить в виде устройства, осуществляющего дифференцирование входного сигнала (рис. 3.12, а). Напряжение на его выходе пропорционально первой производной от входного сигнала.
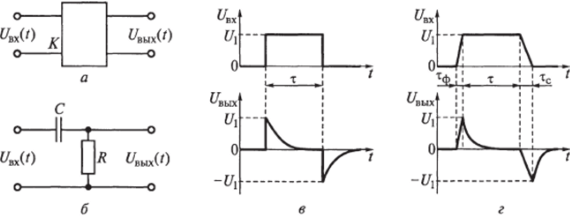
Рис. 3.12. Дифференцирующее устройство (д), дифференцирующая RС-цепь (б) и эпюры напряжений для идеального (в) и реального (г)
импульсов
Связь между напряжениями на входе и выходе можно представить в виде следующей формулы:
![]()
где К — постоянный коэффициент.
Интегрирующие цепи — это цепи, на выходе которых формируется функция, значения которой соответствуют интегралу от функции времени на входе. На входе цепи изменяется ток или напряжение. Интегрирование происходит по времени, т.е. сигнал на выходе цепочки, интегрирующей входное напряжение UBX(t'), имеет следующий вид:
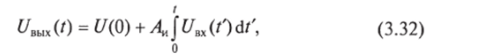
где АИ — постоянный коэффициент интегрирования; /' - {0, /} — обозначение параметра времени, протекающего в процессе интегрирования от 0 до /.
Дифференцирующая RС-цепь — это цепь, состоящая из конденсатора С и резистора R, на выходе которой напряжение пропорционально производной по времени от входного напряжения (рис. 3.12, б).
При подаче на вход RС-цепи напряжения, скачкообразно изменяющегося от 0 до R,, ток в цепи согласно первому закону коммутации и первой формуле (3.1) будет пропорционален производной от входного напряжения и емкости конденсатора:
![]()
Падение напряжения на резисторе R будет пропорционально току и сопротивлению:
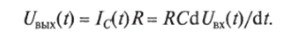
Таким образом, на выходе RС-цепи будет напряжение, пропорциональное первой производной от входного напряжения.
Фронт прямоугольного импульса приводит к резкому скачку напряжения на резисторе и соответственно на выходе дифференцирующей цепи (рис. 3.12, в). Затем конденсатор заряжается, и по мере его насыщения происходит спад зарядного тока. Соответственно падает напряжение на резисторе и выходе RС-цепи. Снижение напряжения на резисторе происходит по экспоненциальному закону с постоянной времени 0 = RC. В момент прохождения среза входного импульса напряжение на резисторе становится равным напряжению на обкладках конденсатора и имеет отрицательный знак (-?/,), так как конденсатор разряжается. По мере разряда конденсатора ток через резистор R и напряжение на его обкладках также уменьшаются по экспоненциальному закону до нуля с постоянной времени 0 = RC.
Реальные импульсы отличаются от идеальных наличием фронта длительностью тф и среза длительностью тс (рис. 3.12, г).
При малых значениях длительности фронта и среза, во время прохождения фронта импульса напряжение на входе RC-цепи линейно возрастает от 0 до Ulf а во время среза — линейно падает от О до
https://studme.org/246378/tehnika/differentsiruyuschie_integriruyuschie_tsepi
Тут с формулами
https://microtechnics.ru/differenciruyushhie-i-integriruyushhie-rc-cepi/