
4сем / Лекции _4_сем pdf / 06_Системы_Сл_Вел_Часть_3_2005
.pdf
Лекция 6 МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В лекции рассматриваются задачи, возникающие при измерении в одном эксперименте не одной, а нескольких случайных величин. Материал предыдущих лекций обобщается на этот случай, приводятся соответствующие способы описания и различные числовые характеристики.
6.1. Многомерные случайные величины
6.1.1.Функция распределения многомерной случайной величины
6.1.2.Дискретные многомерные случайные величины (ДМСВ)
6.1.3.Непрерывные многомерные случайные величины (НМСВ) 6.2. Зависимые и независимые случайные величины
6.2.1.Условные законы распределения 6.3. Числовые характеристики двумерной случайной величины
6.3.1.Корреляционный момент и коэффициент корреляции
6.3.2.Числовые характеристики условных распределений
6.3.3.Линейная регрессия. Прямые линии среднеквадратической регрессии
6.3.4.Линейная корреляция. Двумерный нормальный закон распределения
6.1.Многомерные случайные величины
На одном и том же пространстве событий может быть определена не одна, а несколько случайных величин. Это возникает в случае, когда изучаемый объект характеризуется несколькими случайными параметрами.
Пример:
Составляется модель расходов случайно выбранной семьи на одежду, обувь, питание, транспорт и т.д. Эти затраты являются случайными величинами на одном пространстве элементарных событий.
Пусть Х1 , Х2 ,..., Хn - случайные величины, определенные на множестве элементарных событий Ω. Для удобства будем рассматривать их как координаты случайного n-мерного вектора Х = ( Х1 , Х2 ,..., Хn ) (это упорядоченный
набор n случайных величин Х1, Х2, …, Хn).
Система случайных величин есть функция элементарного события
(Х1, Х2 ,..., Хn )=ϕ(ω), т.е. каждому элементарному событию ω ставятся в
соответствие значения случайных величин: Х1, Х2, …, Хn , полученных в результате опыта.
56 |
Лекция 6 |
ОМногомерной случайной величиной или случайным вектором Х(ω)
называется совокупность случайных величин {X1 (ω), X 2 (ω),..., X n (ω)} . Рас-
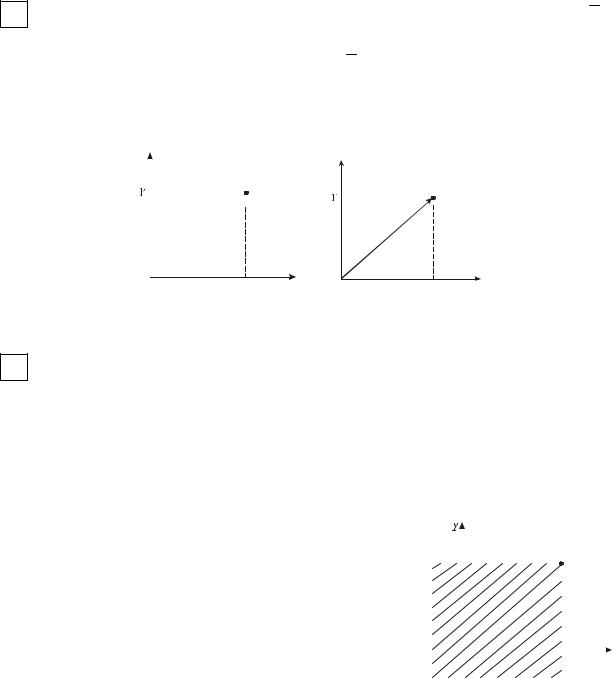
смотрим двумерную случайную величину X (ω) ={X (ω),Y (ω)} .
Геометрическая интерпретация двумерной случайной величиныэто случай- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJJG |
ная точка на плоскости с координатами (X,Y) или случайный вектор OM . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
y |
y |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X,Y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X,Y) |
M |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 X x 0 X x
6.1.1. Функция распределения многомерной случайной величины
О Функцией распределения многомерной случайной величины назы-
вается величина F (x1, x2 ,..., xn ) = P{X1 < x1, X2 < x2 ,..., Xn < xn}.
Событие в фигурных скобках означает произведение событий
{} ={X1 < x1}{X 2 < x2 } ... {X n < xn }, т.е. события происходят одновременно.
Т.о. F (x1 ,..., xn ) = P({X1 < x1} ... {X n < xn }) . Функция распределения F(x1, …, xn) называется совместной функцией распределения одномерных случайных величин.
Рассмотрим двумерную случайную вели-
|
чину |
|
(ω) ={X (ω),Y (ω)} . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
X |
|
|
|
|
|
|
y |
|
|
|
|
|
(x,y) |
|
|
|||||||||||||||||||||||||
|
Совместная функция распределения двух |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
случайных величин (X,Y) есть вероятность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
совместного выполнения двух неравенств |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
F(x,y)=P{X<x,Y<y} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Геометрически это означает вероятность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
X |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
попадания случайной тонки (X,Y) в за- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
штрихованную область. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Основные свойства совместной функции распределения F(x,y): |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1°. Функция F(x,y) есть неубывающая функция своих аргументов. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
2°. |
F (− ∞, y)= F(x,−∞)= F(−∞,−∞)=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Действительно, при x → −∞, или y → −∞ , или |
x → −∞, y → −∞ заштрихо- |
|||||||||||||||||||||||||||||||||||||||
|
ванная область будет смещаться с плоскости |
XOY и вероятность попа- |
|||||||||||||||||||||||||||||||||||||||
|
дания в нее случайной точки будет равна 0 или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3°. |
|
|
F (− ∞, y)= P({X < −∞}{Y < y}) = 0 ; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
F(∞, ∞) =1, т.е. F(∞, ∞) = p({X < ∞}{Y < ∞}) =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Многомерные случайные события |
|
|
|
|
|
|
|
|
|
57 |
|||
|
(заштрихованная область заполняет всю |
|
|
|
|
|
|
|
|
|
|||
|
плоскость, попадание на нее случайной точки |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
- событие достоверное). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
4°. |
Если F1 (x), F2 ( y) - функции распределения од- |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
номерных случайных величин, то: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
F (x, ∞) = F1 (x), |
|
|
|
|
|
|
|
|
|
x |
X |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (∞, y) = F ( y), (по многомерному распределе- |
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
нию можно восстановить одномерное распределение). |
|
|
|
|
|
|
||||||
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
F1 (x) = P{X < x,Y < ∞} = F (x, ∞) , |
т.е. |
событие |
|
|
(a1, b2 ) |
|
(b1,b2 ) |
|
|
||||
|
|
|
|
|
|||||||||
|
X<x, умноженное на достоверное собы- |
b2 |
|
|
|
|
|||||||
|
тие Y<∞, не меняется. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Геометрически |
F1 (x) означает |
вероят- |
a2 |
|
(a1, a2 ) |
(b , a |
) |
|
|
|
||
|
ность попадания точки |
в полуплос- |
|
|
|
|
|||||||
|
|
|
|
1 2 |
|
|
|
|
|||||
5°. |
кость. Аналогично для F2(y). |
|
0 |
|
a1 |
|
|
b1 |
|
|
|||
|
|
|
|
|
|
||||||||
Вероятность |
попадания |
двумерной |
|
|
|
|
|
|
|
|
|
||
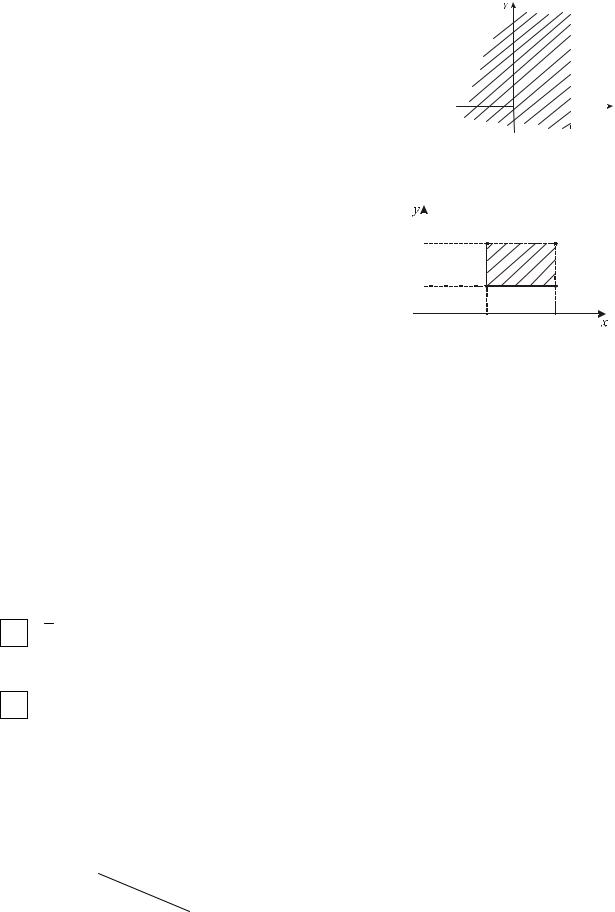
случайной величины в пределы заданного прямоугольника со сторонами a1b1 и a2b2 :
P(a1 ≤ X < b1; a2 ≤Y < b2 ) = F (b1,b2 ) − F (a1 ,b2 ) − F(b1, a2 ) + F(a1, a2 ).
Доказательство:
Вероятность попадания в заштрихованную область равна вероятности попадания в квадрант с вершиной (b1,b2) минус вероятность попадания в квадрант с вершиной ( a1 , b2 ) минус вероятность попадания в квадрант с вершиной (b1,a2), вероятность попадания в квадрант с вершиной в точке (a1,a2) вычли 2 раза, следовательно, ее нужно прибавить.
6.1.2.Дискретные многомерные случайные величины (ДМСВ)
Рассмотрим случай 2-х дискретных случайных величин.
ОX ={X ,Y} называется дискретной, если случайные величины X и Y име-
ют конечное множество возможных значений: X ={x1, x2 ,..., xk },
Y ={y1, y2 ,..., ys }.
ОВероятность того, что случайная величина X примет значение xi, а случайная величина Y – значение yj, называется законом распределения двумерной дискретной случайной величины , т.е. Pij = P{X = xi ;Y = y j }.
Событие есть произведение событий {X = xi }{Y = y j } ;Рij – совместная вероятность.
Закон распределения ДМСВ может быть задан аналогично ряду распределения для одномерной СВ таблицей (или матрицей) распределения.
yi |
y1 |
y2 |
… |
ys |
xi |
|
|
|
|
x1 |
p11 |
p12 |
… |
p1s |

58 |
|
|
|
|
|
Лекция 6 |
|
|
|
|
|
|
|
|
x2 |
p21 |
p22 |
|
p2s |
|
|
… |
… |
… |
… |
… |
|
|
xk |
pk1 |
pk 2 |
… |
pks |
|
!1). Pij ≥ 0, i, j ;
2). ∑Pij =1, |
|
k s |
|
где используется обозначение |
∑∑= ∑ |
. |
|
i, j |
i=1 j=1 i, j |
|
|
Т(о восстановлении одномерной вероятности).
По известной матрице распределения двумерной дискретной случайной величины (X,Y), можно записать ряды одномерных случайных величин X и Y.
P{X = xi } = ∑s |
Pij |
(сумма по строке), |
|
|
|
|
j=1 |
|
|
|
|
|
|
k |
|
|
|
|
|
|
P{Y = y j } = ∑Pij |
(сумма по столбцу). |
|
|
|
||
i=1 |
|
|
|
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
} |
s |
|
|
P{X = xi} = P({X = xi}Ω)= P {X = xi |
∑{Y = y j |
} |
= |
|||
|
|
|
|
j=1 |
|
|
|
s |
|
s |
s |
= P |
∑{X = xi} {Y = y j |
} |
= ∑P({X = xi}{Y = y j })= ∑Pij , |
|
|
j=1 |
|
j=1 |
j=1 |
ч.т.д.
Т.е., чтобы найти вероятность того, что одномерная случайная величина примет значение, например, xi(yj) надо просуммировать вероятности Pij, стоящие в i-той строке (j-том столбце) матрицы распределения.
Пример:
|
|
|
|
|
xi |
|
yj |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
10 |
|
10 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
10 |
|
10 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
yi |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
xi |
0 |
|
1 |
|
||||||
|
|
|
|
|
6 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
P |
4 |
|
6 |
|
|||||||
|
|
10 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
10 |
|
10 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сумма по столбцу |
|
|
|
|
|
|
|
|
|
|
|
|
|
сумма по строке |
||||||||||
Многомерные случайные события |
59 |
6.1.3. Непрерывные многомерные случайные величины (НМСВ)
ОX ={X ,Y} называется непрерывной, если ее функция распределения
F(x,y) является непрерывной функцией и имеет вторую смешанную про-
изводную ∂2 F(x, y) и ∂2 F (x, y) = f (x, y) .
∂x∂y ∂x∂y
Функция f(x,y) называется плотно-
стью распределения (совместной плотностью).
Свойства функции f (x,y):
1.f (x, y) ≥ 0 ;
2.∞∫ ∞∫ f (x, y)dxdy =1.
−∞−∞
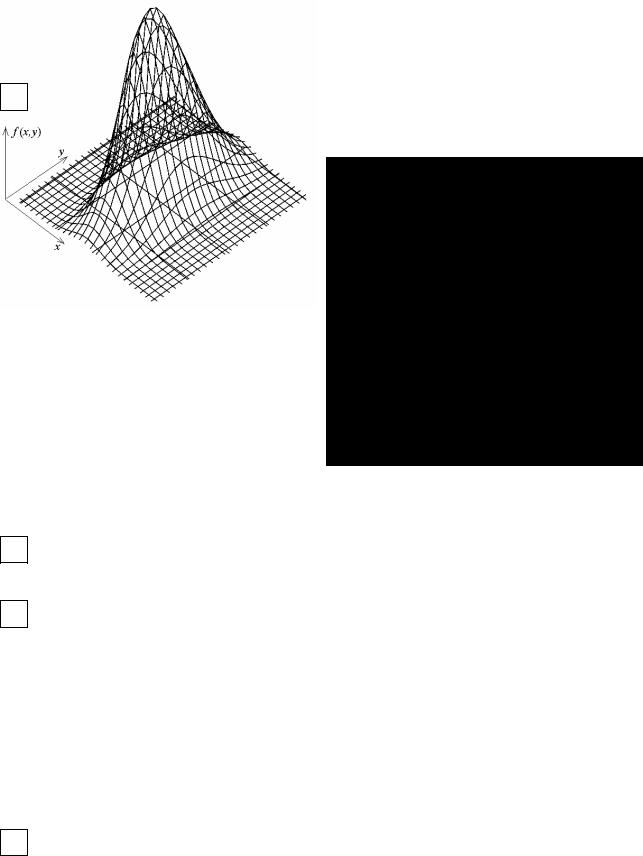
Геометрически совместная плотность распределения – это поверхность. Объем, ограниченный поверхностью распределения и плоскостью OXY, равен 1.
Аналогично случаю одномерной СВ с
элементом вероятности f(x)dx в случае двумерной СВ вводится элемент веро-
ятности f(x,y)dxdy.
ОЭлемент вероятности равен вероятности попадания случайной точки (X,Y) в элементарный прямоугольник dxdy, а вероятность приблизительно равна объему f(x,y)dxdy.
ОВероятность попадания случайной точки (X,Y) в область D плоскости XOY геометрически означает объем тела с основанием D и ограниченного сверху поверхностью f(x,y). P{( X ,Y ) D} = ∫∫ f (x, y)dxdy .
D
Зная совместную плотность распределения двумерной случайной величины f (x, y) , можно найти функцию распределения F(x, y) по формуле
x y
F(x, y) = ∫ ∫ f (x, y)dxdy ,
−∞ −∞
что непосредственно следует из определения плотности распределения двумерной СВ.
Т( о восстановлении одномерной плотности).
Если известен закон распределения НМСВ, то можно найти закон распределения каждой из величин.
f1 (x) = ∞∫ f (x, y)dy; f2 ( y) = ∞∫ f (x, y)dx .
−∞ −∞
60 |
Лекция 6 |
Для получения плотности распределения одномерной случайной величины, надо проинтегрировать совместную плотность от - ∞до ∞ по аргументу, соответствующему другой случайной величине.
Пример:
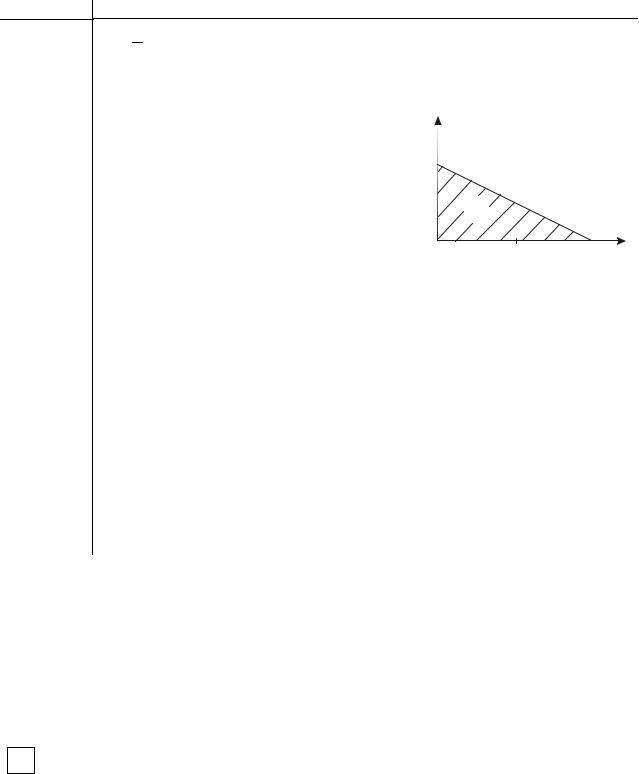
Область D – треугольник с вершинами в точках (0;0); (2;0); (0;1). Двумерная СВ X ={X ,Y} равномерно распределена в области D. Найти плотность рас-
пределения случайных величин X и Y, |
f1 (x) и f2 ( y) . |
|
|
|
|
|
|
|
||||||||||||||||
Решение: |
МСВ |
|
(X,Y) |
распределена равномерно, |
|
следовательно |
||||||||||||||||||
f (x, y) = |
0,(x, y) D; |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a,(x, y) D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+∞ +∞ |
|
|
|
|
|
|
|
|
|
|
∫∫adxdy = |
|
1 |
|
|
|
|
|
|
|
|
|||
∫ ∫ f (x, y)dxdy =1, |
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
−∞ −∞ |
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
D |
|
|
|
|
|
|
|
|
a∫∫dxdy =1, |
a S∆ =1, |
|
a 1 =1 a =1 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
2 |
|
x |
|
По соответствующей теореме |
|
|
|
|
|
|
|
|
|
|||||||||||||||
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [0;2] y 0;1 − |
x |
. |
||||||
f1 (x) = ∫ |
f (x, y)dy . Здесь х – фиксированная точка, |
|||||||||||||||||||||||
|
||||||||||||||||||||||||
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 : y 0;1 |
− |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f (x, y) = |
|
|
|
|
|
2 |
x [0;2]. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1: |
y 0;1− |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1− |
x |
|
|
|
|
|
|
|
|
0 : x [0;2]; |
|
|
|
|
|
|
|
|
||||||
2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f1 (x) = ∫ 1 dy =1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
, |
|
|
|
|
f1 |
(x) = |
|
x |
: x [0;2]. |
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 : y [0;1]; |
|
|
|
|||||||
2(1−y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f2 ( y) = |
∫1 dx = 2(1 − y), y [0;1], |
|
|
|
f2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
( y) = |
2 |
− |
2 y : y |
[ |
] |
|
|||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0;1 . |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6.2. Зависимые и независимые случайные величины
Поставим задачу, обратную теоремам предыдущего параграфа: построение многомерного закона распределения по известным одномерным. В общем виде этого сделать нельзя. Это можно сделать, когда одномерные случайные величины, составляющие многомерную случайную величину, являются независимыми.
ОСлучайные величины X и Y называются независимыми, если их совместная функция распределения равна произведению функций распределения одномерных случайных величин X и Y.
F (x, y) = F1 (x) F2 ( y) .
Многомерные случайные события |
61 |
Т(критерий независимости). Дискретные случайные величины X и Y независимы тогда и только тогда, когда Pij = pi qj ;
Pij = P{X = xi ;Y = y j }; pi = P{X = xi } ; qj = P{Y = y j }.
Таким образом, каждый элемент Pij матрицы распределения двух независимых случайных величин равен произведению соответствующих (i- того и j-того) элементов рядов распределения случайных величин X и Y.
ТНепрерывные случайные величины X и Y независимы тогда и только тогда, когда: f (x, y) = f1 (x) f2 ( y) .
Т.е., совместная плотность распределения равна произведению плотно-
сти распределения одномерных случайных величин.
Пример:
Рассмотрим предыдущий пример ( X ={X ,Y} равномерно распределена на D). Выясним, являются ли величины X и Y зависимыми, для этого проверим выполнение условия f (x, y)= f1 (x) f2 (y).
(x, y) D; |
f (x, y) =1; f1 |
(x) =1− |
x |
; |
f2 ( y) = 2 −2 y , |
||||
|
|||||||||
|
|
x |
|
|
|
2 |
|
|
|
1 |
− |
|
(2 −2 y)≠1, |
|
|
|
|
||
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
Xи Y зависимы.
6.2.1.Условные законы распределения
Если случайные величины X и Y , образующие двумерную случайную величину (X ,Y ), зависимы, для характеристики этой зависимости вводят по-
нятие условного распределения. Напомним определение условной вероятно-
сти: P (B A)= PP((ABA)).
ОУсловным законом распределения случайной величины X , входя-
щей в систему случайных величин (X ,Y ), называется ее закон распре-
деления, найденный при условии, что вторая случайная величина Y приняла |
||||||
определенное значение (или попала в определенный интервал). |
||||||
Рассмотрим вначале случай дискретной двумерной случайной величины. |
||||||
Пусть |
X ={x1 , x2 ,..., xk }, |
Y ={y1 , y2 ,..., ys }, |
pij =P(X = xi ;Y = yj ), |
|||
i =1,2,...,k; |
j =1,2,...,s. Безусловные вероятности компонент |
|||||
|
s |
|
s |
|
|
|
|
Pxi = P (X = xi )= ∑P (X = xi ;Y = y j )= ∑pij , |
|||||
|
j=1 |
|
j=1 |
|
|
|
|
k |
|
k |
|
|
|
|
Py j = P(Y = y j )= ∑P(X = xi ;Y = y j )= ∑pij . |
|
|
|||
|
i=1 |
|
i=1 |
|
|
|
Условная вероятность P(X =xi |
|
Y = yj )= |
P(X = xi ;Y = yj ) |
|||
|
||||||
|
|
|
, или, короче, |
|||
|
P(Y = yj ) |
|
||||
|
|
|
||||

62 Лекция 6
|
|
|
|
|
|
|
|
|
|
|
|
P(xi |
|
yj |
)= |
pij |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pyj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Аналогично, P(Y = yj |
|
X =xi )= |
P(X =xi ;Y = yj ) |
|
|
|
|
или P(yj |
|
|
xi )= |
pij |
. |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
P(X =x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Px |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( Pxi |
|
|
|
P(xi |
|
yj ), Pyj и |
||||||||||||||||
|
! |
Если безусловные и |
|
условные |
вероятности |
|
и |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
P(yj |
|
|
xi )) отличаются, величины |
X |
|
и Y зависимы, |
если совпадают – |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
независимы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Пусть случайная величина (X ,Y ) задана таблицей. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0,05 |
|
|
|
0,15 |
|
|
0,1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0,1 |
|
|
|
|
0,2 |
|
|
0,2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
0,05 |
|
|
|
0,1 |
|
|
0,05 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Найти безусловные законы распределения случайных величин X и Y и ус- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ловный закон распределения X при Y = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
Суммируя, получаем безусловные законы распределения компонент |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
X |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
p |
|
|
0,2 |
|
|
|
|
|
|
0,45 |
|
|
|
|
|
|
|
|
0,35 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
0,3 |
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
Условный закон распределения P(xi |
|
Y =2)= |
|
pi2 |
. |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Py |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
1 |
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PY=2 |
|
0,2 |
|
|
|
|
0,4 |
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
Видно, что безусловный и условный законы распределения не совпадают, |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
следовательно, случайные величины X и Y зависимы. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
Для непрерывной случайной величины (X ,Y ) с плотностью f (x, y) сум- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
мы заменяются интегралами. Безусловные плотности распределения компо- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
нент X |
|
и |
|
Y |
|
равны, |
соответственно, |
f1 (x)= ∫−∞∞ f (x, y)dy , |
||||||||||||||||||||||||||||||
f2 (y)= ∫−∞∞ f (x, y)dx .
Условная плотность распределения (или плотность вероятности услов-
ного распределения) случайной величины X при условии, что случайная величина Y = y определяется как

Многомерные случайные события |
|
|
|
63 |
||
f (x |
|
y)= |
f (x, y) |
= |
f (x, y) |
, f2 (y)≠ 0 . |
|
||||||
|
f2 (y) |
∞ |
||||
|
|
|
|
∫−∞ f (x, y)dx |
|
|
|
|
|
|
|
|
|
Условная плотность обладает всеми свойствами плотности распределения: f (x y)≥ 0, ∫−∞∞ f (x y)dx =1.
Аналогично определяется условная плотность распределения случайной ве- |
||||||
личины Y при условии, что случайная величина X = x : |
||||||
f (y |
|
x)= |
f (x, y) |
= |
f (x, y) |
, f1 (y)≠ 0 . |
|
||||||
|
|
∞ |
||||
|
|
|
f1 (x) |
∫−∞ f (x, y)dy |
|
|
|
|
|
||||
|
|
|
|
|
|
|
Соотношения для условных плотностей могут быть записаны в виде:
f(x, y)= f1 (x) f (y x)= f2 (y) f (x y).
6.3.Числовые характеристики двумерной случайной величины
Для многомерных случайных величин используются числовые характеристики, аналогичные одномерному случаю: математическое ожидание, дисперсия и различные моменты. В многомерном случае числовые характеристики могут описывать не только среднее значение и степень рассеяния компонент, но и степень зависимости между компонентами. Приведем основные определения для дискретных и непрерывных двумерных случайных величин.
ОМатематическим ожиданием двумерной случайной величины (X ,Y ) называется упорядоченная пара чисел (MX ,MY ).
Для дискретной с.в.
|
k |
s |
k s |
|
MX = mx = ∑∑xi pij , MY = my = ∑∑y j pij , pij =P(X = xi ;Y = yj ). |
||||
|
i=1 j=1 |
i=1 j=1 |
|
|
Для непрерывной с.в. |
|
|||
∞ |
∞ |
|
∞ ∞ |
|
MX = ∫ |
∫ xf |
(x, y)dxdy , MY = ∫ ∫ yf (x,y)dxdy , f (x, y) – плотность рас- |
||
−∞ −∞ |
|
−∞ −∞ |
|
|
пределения. |
|
(X ,Y ) называется |
|
|
О Дисперсией |
с.в. |
упорядоченная пара чисел |
||
(DX ,DY ). |
|
|
|
|
Для дискретной с.в. |
k s |
|
||
k |
s |
|
|
|
DX = ∑∑(xi −mx )2 |
pij , DY = ∑∑(y j −my )2 pij . |
|||
i=1 j=1 |
|
i=1 j=1 |
|
|
Для непрерывной с.в. |
|
|||
∞ |
∞ |
|
∞ ∞ |
(y −my )2 f (x, y)dxdy . |
DX = ∫ |
∫ (x −mx )2 f |
(x, y)dxdy , DY = ∫ ∫ |
||
−∞ −∞ |
|
−∞ −∞ |
|
|

64 |
Лекция 6 |
!Геометрическая интерпретация этих понятий следующая: математическое ожидание (mx ,my ) – координаты средней точки, относительно ко-
|
торой разбросаны случайные точки |
(X ,Y ). По |
этой причине точка |
|
|
(mx ,my ) |
иногда называется центром рассеяния. |
Дисперсия (DX ,DY ) |
|
|
показывает, насколько облако точек |
(X ,Y ) разбросано в направлении |
||
|
осей Ox и Oy . |
|
|
|
О |
Начальный момент порядка k+s |
двумерной |
случайной величины |
|
|
(X ,Y ): |
αk ,s = M (X kY s ). |
|
|
|
|
|
||
О Центральный
(X ,Y ): |
µk ,s |
!В соответствии
момент порядка k+s двумерной случайной величины
= M ((X −mx )k (Y −my )s ).
с этим определением:
mx = M (X 1Y 0 )=α1,0 , my = M (X 0Y 1 )=α0,1 ;
DX = M ((X −mx )2 (Y −my )0 )= µ2,0 , DY = M ((X −mx )0 (Y −my )2 )= µ0,2 .
6.3.1. Корреляционный момент и коэффициент корреляции
ОКорреляционный момент с.в. (X ,Y ) (момент связи, ковариация) –
смешанный центральный момент второго порядка: )).yx1,1XY
|
k |
s |
|
Для дискретной с.в. (X ,Y ) |
KXY = ∑∑(xi −mx )(y j −my )pij , |
||
|
i=1 j=1 |
|
|
|
∞ |
∞ |
|
для непрерывной с.в. (X ,Y ) |
KXY = ∫ |
∫ (x −mx )(y −my ) f |
(x, y)dxdy . |
|
−∞ −∞ |
|
|
Для вычисления ковариации удобно использовать формулу |
|
||
KXY = cov (X ,Y )== M (XY )− MX MY , |
|
|
|
которая получается из определения: |
|
|
|
KXY = M ((X −mx )(Y −my ))= M (XY −mxY −my X + my mx )= |
|
||
= M (XY )−mx M (Y )−my M (X )+my mx = M (XY )−my mx . |
|||
Свойства ковариации: |
|
|
|
1°. Ковариация симметрична: KXY |
= KYX . |
|
|
2°. Постоянный множитель можно выносить за знак ковариации: |
|||
cov (cX ,Y )= c cov (X ,Y ) |
= cov (X ,cY ). |
|
|
