
4сем / Лекции _4_сем pdf / 13_14_Корр_и_регр_анализ
.pdf
Лекции 13-14 СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ
ЗАВИСИМОСТЕЙ. КОРРЕЛЯЦИОННЫЙ
ИРЕГРЕССИОННЫЙ АНАЛИЗ
13.Основы корреляционного анализа
13.1.Основные понятия
13.2.Элементы теории корреляции. Анализ парных связей
13.3.Оценка показателя связи по выборочным данным. Корреляционное поле
13.4.Анализ коэффициента корреляции
13.4.1.Точечная оценка коэффициента корреляции
13.4.2.Интервальная оценка коэффициента корреляции
ипроверка значимости
14.Основы регрессионного анализа
14.1.Условные средние. Выборочные уравнения регрессии
14.2.Корреляционная таблица. Выборочные линии регрессии
14.3.Линейная регрессия. Выборочный коэффициент корреляции
13.Основы корреляционного анализа
13.1. Основные понятия
При решении многих задач требуется установить и оценить зависимость между переменными величинами, которые могут быть и случайными. Рассмотрим несколько примеров.
Пример:
Двое играют в кости. X1 – число очков у первого игрока, X 2 – у второго, Y
– сумма, которую получает (или платит) первый игрок.
Пример:
Y – величина износа (в мм) протектора шина на автомобилях определенного типа после 10000 км пробега, X1 – величина нагрузки (в кг) на колесо авто-
мобиля, X 2 – тип протектора (используется три типа протекторов). Если установить степень влияния X1 и X 2 на Y , то можно дать рекомендации по продлению долговечности шины.

|
Статистическое исследование зависимостей. Корреляционный и регрессионный анализ |
135 |
||||
|
Пример: |
|
|
|
|
|
|
Пусть Y1 |
– производительность химической установки (в т/ч), Y2 – процент |
|
|||
|
брака готовой продукции. Технолог предполагает, что на переменные Y1 и Y2 |
|||||
|
влияют |
в наибольшей степени |
такие технологические |
параметры, |
как: |
|
|
X1 – влажность сырья (в %), X 2 |
– температура в реакторе установки, X3 – |
||||
|
содержание примеси (в %). Если найти вид зависимости Y1 |
и Y2 от X1 , |
X 2 , |
|||
X3 , то можно подобрать оптимальный технологический режим (при котором,
например, при допустимом проценте брака производительность будет максимальной или при заданной производительности минимальным будет процент брака).
Пример:
Пусть Y – успеваемость студентов по некоторой дисциплине (измеряемая, например, средним баллом на экзамене). Ректорат проводит обследование студентов данного вуза с целью установления наиболее значимых факторов, влияющих на Y . В результате предварительного анализа сделано предполо-
жение о том, что этими факторами могут быть: X1 – время, затрачиваемое студентом на самостоятельную работу, X 2 – количество пропущенных занятий, X3 – величина стипендии. Существует ли взаимосвязь между факторами X1 , X 2 , X3 ? В какой мере они оказывают влияние на успеваемость?
Приведенные примеры не исчерпывают все возможные постановки задач рассматриваемого типа, но позволяют отметить некоторые закономерности.
1.Случайные величины могут быть связаны строгой функциональной зависимостью (пример 1: хотя Y и случайна, но однозначно зависит от X1 и X 2 ).
2.Зависимое переменное Y может быть случайной величиной, даже если переменные X1 , X 2 , …, X k таковыми не являются, так как значение Y определя-
ется не только значениями X1 , X 2 , …, X k , которые исследователь выделил (по
его мнению, они являются определяющими), но и многими другими неучтенными факторами, а также ошибками измерений. Это означает, что связь между Y и X1 , X 2 , …, X k является не функциональной, а стохастической – измене-
ние переменных X1 , X 2 , …, X k влияет на значения переменного Y через изменение закона распределения случайной величины Y . Если изменение X1 , X 2 , …, X k приводит к изменению среднего значения Y , связь называется корре-
ляционной.
3.Некоторые переменные могут иметь количественный характер, а некоторые – качественный (пример 2).
4.Нас может интересовать либо зависимость переменного Y от переменных X1 , X 2 , …, X k , либо взаимозависимость между переменными (необяза-

136 Лекции 13–14
тельно между всеми). Так, в примере 4 может существовать взаимозависимость между переменными X1 , X 2 и X3 .
Перечисленные особенности приводят к различным постановкам задач статистического исследования зависимостей, которые упрощенно можно классифицировать следующим образом:
1)задачи корреляционного анализа – задачи исследования наличия взаимосвязей между отдельными группами переменных;
2)задачи регрессионного анализа – задачи, связанные с проверкой гипотезы о наличии приближенной количественной зависимости между переменным Y и одним или несколькими переменными X1 , X 2 , …, X k , которые носят ко-
личественный характер.
3) |
задачи |
дисперсионного анализа – задачи, в которых переменные |
X1 , |
X 2 , …, |
X k , носят качественный или именованный характер, а исследуется |
и устанавливается степень их влияния на переменное Y .
13.2. Элементы теории корреляции. Анализ парных связей
Рассмотрим задачу о выборе показателя стохастической связи между дву-
мя случайными величинами X и Y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть система (X ,Y ) |
имеет двумерный нормальный закон распределения |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
(y −my ) |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
− |
|
|
(x−mx ) |
|
+ |
|
−2rxy |
x−mx y−my |
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
2 |
|
σx σy |
|
|||||||
f (x, y )= |
|
|
|
|
|
|
e |
|
2(1−rxy ) |
|
σx |
|
|
σy |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||
2πσ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
σ |
y |
1−r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где mx , my - математические ожидания, |
σx , σy |
|
– среднеквадратические откло- |
|||||||||||||||||||||||
нения, rxy – коэффициент корреляции величин X и Y . |
|
|
|
|||||||||||||||||||||||
Условная плотность распределения случайной величины Y |
при условии, |
|||||||||||||||||||||||||
что X = x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(y−mY |
|
x )2 |
|
|
|
|
|
||||
|
f (y |
|
x)= |
|
|
|
1 |
e− |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2σY2 |
|
x |
|
, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
σY |
|
x 2π |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
также является плотностью нормального распределения с параметрами mY x (условное математическое ожидание) и σY2 x (условная дисперсия) при значении
X = x , которые связаны с параметрами исходного распределения следующим образом:
M (Y |
|
X = x)= mY |
|
x |
= my −r |
σy |
(m −ax ), |
||||
|
|||||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
x |
|
D (Y |
|
X = x)=σY2 |
|
x =σy 2 (1 −r2 ). |
|||||||
|
|||||||||||
|
|
||||||||||
В этом случае линия регрессии является прямой, а условная дисперсия не |
|||||||||||
зависит от x . |
|
|
|
||||||||
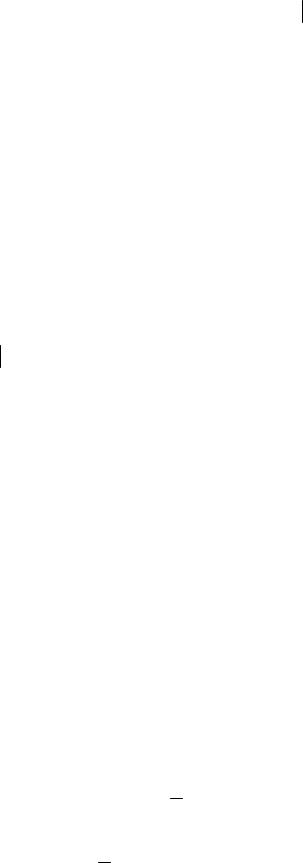
Статистическое исследование зависимостей. Корреляционный и регрессионный анализ |
137 |
Если закон распределения системы (X ,Y ) отличен от нормального, то характер изменения условного математического ожидания M (Y X = x)= f (x)
может быть и нелинейным. Напомним, что эта функция называется функцией регрессии.
Рассмотрим отклонение возможных значений с.в. Y от ее среднего, my .
Его можно разбить на два слагаемых:
y −my = (f (x)−my )+(y − f (x)),
отклонение функции регрессии f (x) в точке x от математического ожидания my и отклонение возможного значения y от значения функции регрессии в точке x .
Покажем, что рассеяние σy2 случайной величины Y относительно ее мате-
матического ожидания есть сумма двух слагаемых: математического ожидания квадрата отклонения Y от ее условного математического ожидания f (X ) и
математического ожидания квадрата отклонения f (X ) от my .
M (f (X ))= M (M (Y X ))= M (Y )= my ,
D(Y )=σy 2 = M ((Y −my )2 )= M (((f (X )−my )+(Y − f (X )))2 )=[0,1]
=M ((Y − f (X ))2 )+2M ((f (X )−my )(Y − f (X )))+ M ((f (X )−my )2 )=
=M ((Y − f (X ))2 )+ M ((f (X )−my )2 ),
так как M ((f (X )−my )(Y − f (X )))= 0 .
Докажем последнее равенство для непрерывных случайных величин X и Y , предполагая, что их совместная плотность распределения p (x, y )≠ 0:
M ((f (X )−my )(Y − f (X )))= ∫∞ |
∫∞ (y − f (x))(f (x)−my )p (x, y)dxdy = |
|||||||
|
|
−∞ −∞ |
|
|
|
|
||
∞ |
∞ |
p (x, y) |
∞ |
p (x, y) |
|
|
||
= ∫ |
(f (x)−my )pX (x)dx ∫ y |
dy − f (x) ∫ |
dy |
= 0, |
||||
pX (x) |
pX (x) |
|||||||
−∞ |
−∞ |
−∞ |
|
|
||||
|
∞ |
|
p (x, y ) |
dy = f (x), |
∞ |
p (x, y ) |
|
|
так как |
∫ |
y |
∫ |
dy =1. |
||||
|
|
|||||||
|
−∞ |
|
pX (x) |
−∞ |
pX (x) |
|||
Если ввести обозначения
σ2f = D (f (X ))= M ((f (X )−my )2 ), σ2y = M ((Y − f (X ))2 ),
то полученный результат можно представить в виде
2
σy2 =σ2f +σ y .

138 |
Лекции 13–14 |
Из этого равенства следует, что связь между X и Y тем теснее, чем больший вклад в дисперсию σy2 вносит слагаемое σ2f , порожденное функцией рег-
рессии f (x)= M (Y X = x). В качестве такой характеристики принимается отношение
|
|
|
|
σ2f |
|
|
|
|
2y , |
|
|
|
|
IYX = |
= 1− |
σ |
|
||||
|
|
|
σ2 |
|
||||||
|
|
|
|
|
σ2 |
|
||||
|
|
|
|
y |
|
|
|
y |
|
|
называемое корреляционным отношением переменного Y |
по переменному |
|||||||||
|
X . |
|
|
|
|
|
|
0 ≤ IYX2 ≤1. Если |
IYX2 =1, т.е., |
|
|
|
Из определения |
следует, |
что |
|
|
||||
|
|
2y = M ((Y − f (X ))2 )= 0, это означает, |
что X и Y связаны функциональной |
|||||||
σ |
||||||||||
зависимостью, Y = f (X ), если IYX2 |
= 0 , линия регрессии – горизонтальная пря- |
|||||||||
мая, изменение с.в. X |
не меняет математического ожидания с.в. Y (в частно- |
|||||||||
сти, это может быть, если X и Y независимы). |
I XY2 переменного |
|||||||||
|
|
Аналогично определяется и корреляционное отношение |
||||||||
Xпо переменному Y .
!Для выяснения степени тесноты связи необходимо рассматривать оба корреляционных отношения, I XY2 и IYX2 . Пусть переменные X и Y связаны функциональной зависимостью, Y = X 2 , и X принимает значения -1, 0, 1 с вероятностями 1/3 каждое. В этом случае IYX2 =1, I XY2 = 0 (в силу симметричности параболы относительно оси значений y и симметричности рас-
пределения X ). Если ограничиться только вычислением I XY2 , то может возникнуть ложное впечатление, что X и Y независимы.
Ранее при рассмотрении систем случайных величин вводился коэффициент корреляции
rXY = M ((X −mx )(Y −my )).
Для системы нормально распределенных величин X и Y
I XY2 = IYX2 = rXY2 .
Действительно, для нормально распределенной пары (X ,Y ) условная дисперсия
D (Y X = x)=σY2 x =σy 2 (1−rXY2 )= M ((Y − M (Y X = x))2 X = x)=
= M ((Y − f (X ))2 X = x)= M ((Y − f (X ))2 )=σ2y ,

Статистическое исследование зависимостей. Корреляционный и регрессионный анализ |
139 |
||||||||
и так как |
|
|
2y |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
2 |
=σy2 (1− IYX2 ), |
|
|||
|
|
|
|
|
|
||||
|
|
|
IYX2 =1− σ2 σ y |
|
|||||
|
|
|
|
|
y |
|
|
|
|
откуда I 2 = r2 . Аналогично доказывается вторая часть равенства. |
|
||||||||
|
|
YX |
XY |
|
|
|
|||
|
В общем случае показатели I |
2 |
и r2 связаны неравенствами: |
|
|||||
|
|
|
|
|
|
|
XY |
XY |
|
|
|
|
|
|
0 ≤ r2 |
≤ I 2 ≤1. |
|
||
|
|
|
|
|
|
XY |
XY |
|
|
|
При этом возможны следующие варианты: |
|
|||||||
а) |
r2 |
= 0, если Y и X независимы, но обратное (в общем случае) неверно; |
|||||||
|
XY |
|
|
|
|
|
|
|
|
б) |
r2 |
= I 2 |
=1 тогда и только тогда, когда имеется строгая линейная функ- |
||||||
|
XY |
XY |
|
|
|
|
|
|
|
циональная зависимость Y от X ; |
|
|
|
||||||
в) |
r2 |
≤ I 2 |
=1 тогда и только тогда, когда имеется строгая нелинейная функ- |
||||||
|
XY |
XY |
|
|
|
|
|
|
|
циональная зависимость Y от X ; |
|
|
|
||||||
г) |
r2 |
= I 2 |
<1 тогда и только тогда, когда регрессия Y по X строго линейна, |
||||||
|
XY |
XY |
|
|
|
|
|
|
|
но нет функциональной зависимости; |
|
||||||||
д) |
r2 |
< I 2 |
<1 указывает на то, что нет строгой функциональной зависимо- |
||||||
|
XY |
XY |
|
|
|
|
|
|
|
сти, а некоторая нелинейная кривая регрессии приближает зависимость лучше, чем любая прямая линия.
Итак, в качестве показателя стохастической связи между двумя случайными количественными переменными X и Y следует выбрать корреляционное
отношение I XY2 (или IYX2 ), если закон распределения системы (X ,Y ) неизвестен; если есть основания считать, что система (X ,Y ) имеет нормальный закон распределения, то вместо корреляционного отношения следует использовать коэффициент корреляции rXY .
13.3. Оценка показателя связи по выборочным данным. Корреляционное поле
После выбора показателя стохастической связи задача корреляционного анализа состоит в нахождении его оценки (точечной и интервальной), а также в проверке статистической гипотезы о значимом отличии его от нуля на основе экспериментальных данных.
Пусть в результате эксперимента для системы (X ,Y ) получена выборка значений (xi , yi ), =1,2,...,n .
При изучении корреляционной зависимости двух случайных величин (X ,Y ) по выборке
(xi , yi ) общую картину их взаимной изменчивости можно получить, изобразив на координат-

140 |
Лекции 13–14 |
ной плоскости все точки. Это изображение называют корреляционным полем. Уже по виду корреляционного поля часто можно сделать вывод о наличии и характере связи между случайными величинами Y и X . Так, на первом ри-
сунке выборочные точки лежат внутри некоторого эллипса (эллипса рассеяния) с осями, параллельными координатным. Следовательно, с изменением, например, X величина Y не будет менять своего
условного распределения, т.е. X и Y , повидимому, некоррелированы.
Напротив, на втором рисунке видно, что условное математическое ожидание
M (Y x)= f (x) имеет линейный характер изменения, и, значит, следует ожидать, что коэффициент корреляции rXY близок к еди-
нице.
На третьем рисунке расположение точек (xi , yi ) говорит о наличии нелинейного ха-
рактера изменения f (x), и, следовательно, коэффициент корреляции rXY может оказаться близким к нулю, а корреляционное отношение I XY – близким к единице.
13.4. Анализ коэффициента корреляции
13.4.1. Точечная оценка коэффициента корреляции
Пусть экспериментальные данные представлены в несгруппированном виде. Тогда в качестве точечной оценки коэффициента корреляции rXY берут его выборочное значение rXY* :
|
|
|
|
∑(xi − X )(yi −Y ) |
||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
||
* |
* |
|
|
i=1 |
|
|
|
|
|
|
|
|||
rXY |
= r |
= |
|
|
|
|
|
|
. |
|||||
n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
n |
||||||
|
|
|
∑(xi − |
|
)2 |
∑(yi − |
|
)2 |
|
|||||
|
|
X |
Y |
|||||||||||
|
|
|
i=1 |
|
|
|
|
|
i=1 |
|||||
Пример:
Найдем выборочное значение коэффициента корреляции для пары случайных величин (X ,Y ), где X – рост (в см), а Y – масса тела (в кг) выбранного наугад студента. Выборка объема n =15 представлена в таблице (столбцы 2 и 5).

Статистическое исследование зависимостей. Корреляционный и регрессионный анализ |
141 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
Рост, |
|
|
|
см |
|
|
|
|
|
|
|
|
Масса, |
|
|
кг |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
(xi − |
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
(yi − |
|
)2 |
(xi − |
|
)(yi − |
|
) |
|
||||
|
наблюдения |
xi |
|
|
xi − |
|
|
|
|
|
y j |
|
|
yi − |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
X |
|
X |
|
|
Y |
|
|
Y |
X |
Y |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
165 |
|
-8,33 |
|
69,44 |
72,9 |
|
|
9,83 |
|
|
96,69 |
|
-81,94 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
171 |
|
-2,33 |
|
5,44 |
|
48,4 |
|
-14,67 |
215,11 |
|
34,22 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
182 |
|
8,67 |
|
75,11 |
66,3 |
|
|
3,23 |
|
|
10,45 |
|
28,02 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4 |
165 |
|
-8,33 |
|
69,44 |
64,1 |
|
|
1,03 |
|
|
1,07 |
|
|
-8,61 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
5 |
183 |
|
9,67 |
|
93,44 |
62,7 |
|
|
-0,37 |
|
|
0,13 |
|
|
-3,54 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
6 |
180 |
|
6,67 |
|
44,44 |
76,0 |
|
|
12,93 |
|
167,27 |
|
86,22 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
7 |
183 |
|
9,67 |
|
93,44 |
73,8 |
|
|
10,73 |
|
115,20 |
|
103,76 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
8 |
166 |
|
-7,33 |
|
53,78 |
50,6 |
|
-12,47 |
155,42 |
|
91,42 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
9 |
173 |
|
-0,33 |
|
0,11 |
|
52,3 |
|
-10,77 |
115,92 |
|
3,59 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
10 |
172 |
|
-1,33 |
|
1,78 |
|
56,5 |
|
|
-6,57 |
|
|
43,12 |
|
8,76 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
11 |
174 |
|
0,67 |
|
0,44 |
|
66,8 |
|
|
3,73 |
|
|
13,94 |
|
2,49 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
12 |
170 |
|
-3,33 |
|
11,11 |
61,6 |
|
|
-1,47 |
|
|
2,15 |
|
|
4,89 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
13 |
164 |
|
-9,33 |
|
87,11 |
72,8 |
|
|
9,73 |
|
|
94,74 |
|
-90,84 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
14 |
168 |
|
-5,33 |
|
28,44 |
52,6 |
|
-10,47 |
109,55 |
|
55,82 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
15 |
184 |
|
10,67 |
|
113,78 |
68,6 |
|
|
5,53 |
|
|
30,62 |
|
59,02 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Сумма |
2600 |
|
|
|
|
|
|
747,33 |
946,0 |
|
|
|
|
|
|
1171,39 |
|
293,27 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
среднее |
173,33 |
|
|
|
|
|
|
|
|
|
|
|
|
63,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
СКО |
|
|
|
|
|
|
|
27,34 |
|
|
|
|
|
|
|
|
|
34,23 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вначале находим выборочные средние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
= 1 |
∑xi =173,3 и |
|
= |
1 |
∑yi = 63,1, |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
X |
Y |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
i |
|
|
|
n |
i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
затем вычисляем разности xi − |
|
и (столбцы 3 и 6), их квадраты (столбцы 4 и |
||||||||||||||||||||||||||||||||
|
X |
||||||||||||||||||||||||||||||||||
|
7) и произведения (столбец 8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Затем находим суммы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
∑(xi − |
|
)2 = 747,3, ∑(yi − |
|
)2 =1171,4 , |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
X |
Y |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∑15 (xi − X )(yi −Y )= 293,3
i=1
ивычисляем выборочный коэффициент корреляции:
* |
|
293,3 |
|
r |
= |
|
= 0,313 . |
747,3 1171,4 |
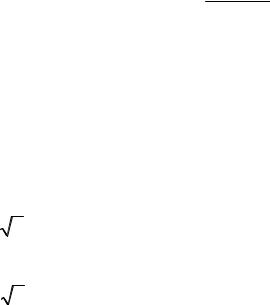
142 |
Лекции 13–14 |
13.4.2. Интервальная оценка коэффициента корреляции и проверка значимости
При построении доверительного интервала для коэффициента корреляции и проверки его значимости будем предполагать, что генеральная совокупность имеет двумерный нормальный закон распределения. В этом случае
оценка коэффициента корреляции r* (xi , y j ) имеет асимптотически нормальный
закон распределения с математическим ожиданием M r* (xi , y j ) ≈ r − r (1−r2 )
2n
и дисперсией D r* (xi , y j ) ≈ (1 −r2 )2 . n
Используя общий метод построения доверительного интервала, основанный на нормальном законе распределения соответствующей оценки при доверительной вероятности γ =1−α , можно получить следующие значения для
нижней и верхней границ интервальной оценки:
* |
|
r* (1− |
(r* )2 ) |
|
|
1−(r* )2 |
|||||
r ≈ r |
+ |
|
|
−u |
α |
|
|
, |
|||
2n |
|
|
|||||||||
|
|
|
|
1− |
2 |
|
n |
||||
|
|
* |
|
r* (1 − |
(r* )2 ) |
|
1 −(r* )2 |
||||
|
|
|
|
||||||||
r ≈ r |
+ |
|
|
+u |
α |
|
|
, |
|||
2n |
|
||||||||||
|
|
|
|
1− |
2 |
|
n |
||||
где r* – точечная оценка коэффициента корреляции, u |
α – квантиль стандарт- |
|
1− |
2 |
|
ного нормального распределения уровня 1−α . |
||
|
||
2 |
|
|
Следует заметить, что этими оценками можно пользоваться при достаточ- |
||
но больших объемах выборки (не менее 500). При малых объемах выборки можно использовать построение доверительного интервала для rXY , основанное на преобразовании Р.Фишера:
|
1 |
|
1 |
+r* |
|
z = arcth (r |
* |
). |
|
||
z = |
2 ln |
1 |
−r* |
или |
|
|
|||||
|
|
|
|
|
|
|
1 |
1+r* (xi , y j ) |
|
||
Оказывается, |
что случайная величина |
Z = |
2 ln |
|
|
уже при не- |
|||||
1−r* |
(xi , y j ) |
||||||||||
больших значениях n приблизительно распределена по нормальному закону с параметрами
M (Z )≈ |
1 ln 1+r |
+ |
|
r |
, D (Z )≈ |
|
|
1 |
|
. |
||||
2 |
(n −1) |
n |
−3 |
|||||||||||
|
2 1−r |
|
|
|
|
|
|
|||||||
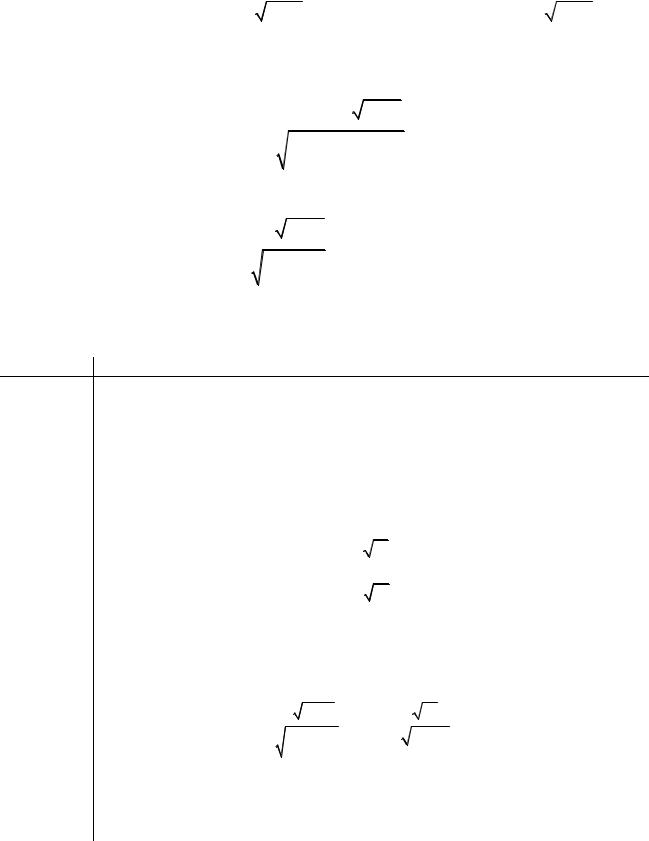
Это приводит к представлению |
|
|
|
|
|
|
|
|
|
|
||||
|
r = th z , |
|
|
|
= th |
|
, |
|
|
|
||||
|
|
r |
z |
|
|
|
||||||||
Статистическое исследование зависимостей. Корреляционный и регрессионный анализ |
|
143 |
||||||||||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
||
|
1 |
|
1+r* |
|
|
|
r* |
|
|
α |
|
|
|
|
|
|
1 |
|
1 + r* |
|
|
|
r* |
|
|
|
α |
|
|
|||||||
|
|
|
|
|
|
|
|
1− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1− 2 |
|
|
||||||||||||
z = |
ln |
+ |
|
|
− |
|
, |
|
z |
= |
ln |
+ |
|
|
|
|
+ |
|
. |
|||||||||||||||||
|
|
* |
|
( |
) |
|
n |
|
3 |
|
|
* |
|
( |
|
) |
n |
|
3 |
|||||||||||||||||
|
2 1−r |
|
2 |
|
|
|
− |
|
|
|
|
|
2 1 −r |
|
2 |
n − |
|
− |
|
|||||||||||||||||
|
|
|
n −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||
При проверке статистической гипотезы |
H0 : rXY |
= 0 (т.е. |
гипотезы о том, |
|||||||||||||||||||||||||||||||||
что нормально распределенные случайные величины |
X и Y |
независимы ис- |
||||||||||||||||||||||||||||||||||
пользуют критерий |
|
|
|
|
|
|
|
|
|
r* (xi , y j ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
t = |
|
n −2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 −(r* (xi , y j ))2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Эта случайная величина имеет распределение Стьюдента с |
|
n −2 |
степенями |
|||||||||||||||||||||||||||||||||
свободы. Если окажется, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r* |
|
n −2 |
< t |
α (n −2), |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 −(r* )2 |
1− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
то гипотезу H0 |
принимают при уровне значимости α . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Пример:
В предыдущем примере была найдена точечная оценка коэффициента корреляции r* = 0,313 . Определим нижнюю и верхнюю границы доверительного интервала при γ = 0,9 и проверим гипотезу H0 : rXY = 0 на уровне значимости
α = 0,1.
Используем первый вариант получения интервальной оценки. По таблице
квантилей нормального распределения значение u |
|
α = u0,95 =1,65 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
1− |
2 |
||
|
|
|
|
|
|
0,902 |
|
|
|
|
|||
r = 0,313 +0,009 −1,65 |
= 0,322 −0,384 ≈ −0,062 , |
||||||||||||
|
|
|
|
|
|
15 |
|
|
|
|
|
||
r = 0,313 +0,009 +1,65 |
0,902 |
= 0,322 +0,384 ≈ 0,706 . |
|||||||||||
|
|
|
|
|
|
15 |
|
|
|
|
|
||
Второй метод (для малых выборок) дает более надежный результат: |
|||||||||||||
r = th z ≈ −0,162 , |
|
r |
=th |
z |
≈ 0,658 . |
|
|
||||||
Для проверки гипотезы H0 : rXY |
= 0 по |
таблице |
|
квантилей распределения |
|||||||||
Стьюдента находим квантиль t0,95 (13)=1,77 и сравниваем со значением |
|||||||||||||
t* = |
r* |
n −2 |
|
= 0,313 |
|
13 |
|
=1,19 . |
|||||
1− |
(r* )2 |
|
0,902 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
Поскольку 1,19 <1,77 нет оснований отклонить гипотезу H0 , т.е., на уровне значимости α = 0,1 X и Y можно считать независимыми.
Аналогично производится анализ корреляционного отношения: получение точечной и интервальной оценок и проверка значимости оценки.
