
4сем / ПП_4_сем_pdf / ПП _01 _Элементы теории множеств и комбинаторики
.pdf
должны быть нечетными. Существует 5 6 6 3 =540 таких чисел.
ПП 1.№6. Сколькими способами можно распределить 5 шаров по 8 ящикам?
РЕШЕНИЕ:
Размещение r = 5 шаров по n =8 ящикам равнозначно выбору ящика для каждого шара. Для 85 5 шаров мы имеем 8 независимых выборов,
поэтому r = 5 шаров можно разместить в n =8
ящиках n n n ... n = nr =85 различными способами.
r
ПП 1.№7. Сколькими способами можно расставить на полке три книги (А, В и С)?
РЕШЕНИЕ:
а) Изобразим все возможные размещения в виде дерева из точки О и подсчитаем их:
6
Число способов расстановки книг равно шести. б) Изобразим три места на полке:
На первое место мы можем поместить или А, или В, или С, поэтому первое место мы
можем заполнить тремя способами, второе – двумя, третье – одним: 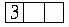

Общее число способов расстановки находится умножением 3 2 1 = 6 .
в) Число способов расставить книги равно числу перестановок множества из трех элементов:
Ρ3 =3! =3 2 = 6 .
ПП 1.№8. Сколько различных четырехзначных чисел можно получить из цифр: 3, 4, 5, 6?
РЕШЕНИЕ:
Числа отличаются друг от друга только порядком 24 входящих в их написание цифр, их столько, сколько можно составить перестановок из четырех элементов: P4 = 4! = 24.
11

ПП 1.№9. |
Сколькими способами можно упорядочить |
|
|||||
|
множество {1, 2, 3, … 2n} так, чтобы каждое четное |
|
|||||
|
число имело четный номер? |
|
|
|
|
|
|
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
Число мест с четными номерами равно n . Четные |
|
|||||
|
числа можно расставить на них n! способами. При |
|
|||||
|
этом по основному принципу комбинаторики мы |
(n!)2 |
|||||
|
должны учесть, что если мы упорядочиваем 2n |
|
|||||
|
чисел, среди которых n нечетных, это число должно |
|
|||||
|
быть умножено на n! способов размещения |
|
|||||
|
нечетных чисел на местах с нечетными номерами. |
|
|||||
|
Следовательно, существует |
n! n! = |
( |
n! |
2 |
способов |
|
|
|
) |
|
|
|||
|
таких упорядочений. |
|
|
|
|
|
|
ПП1.№10. |
Сколько можно составить перестановок из n |
|
|||||
|
элементов, в которых данные 2 элемента не стоят |
|
|||||
|
рядом? |
|
|
|
|
|
|
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
Имеется n мест. Посчитаем число способов |
|
|||||
|
размещения n элементов на этих местах, когда |
|
|||||
|
элементы a и b стоят рядом. Число способов |
|
|||||
|
размещения элемента b справа от элемента a равно |
|
|||||
|
(n-1), так как попарно они могут занять первое- |
|
|||||
|
второе, второе-третье, …, (n-1) и n места. |
|
|||||
|
Элементы a и b можно поменять местами, |
|
|||||
|
следовательно, существует 2(n −1)способа |
(n −2) |
|||||
|
размещения a и b рядом. |
|
|
|
|
|
(n −1)! |
|
Кроме того, по основному принципу |
|
|
|
|||
|
комбинаторики нужно учесть, что каждому из этих |
|
|||||
|
способов соответствует (n-2)! перестановок других |
|
|||||
|
элементов. |
|
|
|
|
|
|
|
Следовательно, число перестановок, в которых a и |
|
|||||
|
b стоят рядом, равно: |
|
|
|
|
|
|
|
2 (n −1)(n −2)! = 2 (n −1)! |
|
|
|
|||
Число всех возможных перестановок равно n!. Искомое число перестановок, в которых a и b не стоят рядом равно разности:
n! −2 (n −1)! = (n −2)(n −1)!.
ПП 1.№11. Сколькими способами можно рассадить 4 студента на 25 местах?
РЕШЕНИЕ:
Искомое число способов равно числу размещений 303600 из 25 по 4:
Α425 = 25 24 23 22 =303600 .
12
ПП 1.№12. |
Студенту нужно сдать 4 экзамена за 8 дней. |
|
|||||
|
Сколькими способами можно это сделать? |
|
|||||
|
РЕШЕНИЕ: |
|
|
|
|
||
|
а) Искомое число способов равно числу |
|
|||||
|
четырехэлементных упорядоченных подмножеств |
а) 1680, |
|||||
|
(дни сдачи экзаменов) множества из 8 экзаменов: |
б) 840 |
|||||
|
|
|
|
|
Α84 =8 7 6 5 =1680 . |
|
|
|
б) Если последний экзамен нужно сдавать на |
|
|||||
|
восьмой день, то число способов равно |
|
|||||
|
|
|
|
4 A73 4 = 4 7 6 5 4 =840 . |
|
||
ПП 1.№13. |
Колода карт для игры в бридж состоит из 52 карт, |
|
|||||
|
которые делятся на четыре равные группы по |
|
|||||
|
масти. Карты каждой масти различают по |
|
|||||
|
значению. Имеется 13 значений (2, 3, … 10, валет, |
|
|||||
|
дама, король, туз). Сколько комбинаций карт может |
|
|||||
|
быть у одного игрока при игре в бридж, если |
6 1011 |
|||||
|
порядок карт у игрока не существенен? |
|
|||||
|
РЕШЕНИЕ: |
|
|
|
|
||
|
Число различных комбинаций карт у одного игрока |
|
|||||
|
равно C5213 = |
|
52! |
= 635013559600 . |
|
||
|
|
|
|
||||
|
|
|
13! 39! |
|
|||
ПП 1.№14. |
Дана прямоугольная сетка квадратов размером m+n |
|
|||||
|
(«шахматный город»). Каково число различных |
|
|||||
|
кратчайших путей по сторонам ячеек сетки из |
|
|||||
|
левого нижнего угла в правый верхний угол? |
|
|||||
|
РЕШЕНИЕ: |
|
|
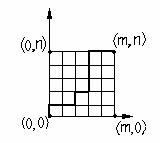
Каждый кратчайший путь |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из точки (0,0) |
|
|
|
|
|
|
|
в точку (m,n) состоит из |
Cmn +n |
|
|
|
|
|
|
(m+n) отрезков, |
|
|
|
|
|
|
|
причем среди них есть m |
|
|
|
|
|
|
|
горизонтальных |
|
|
|
|
|
|
|
и n вертикальных. Разные |
|
|
|
|
|
|
|
|
|
|
пути отличаются лишь порядком их чередования. |
|
|||||
|
Общее число способов, которыми из m+n отрезков |
|
|||||
|
можно выбрать n вертикальных, равно Cmn +n =Cmm+n . |
|
|||||
ПП 1.№15. |
Сколькими способами из команды в 7 человек |
|
|||||
|
а) можно выбрать трех лучших, |
|
|||||
|
б) наградить их золотой, серебряной и бронзовой |
35, |
|||||
|
медалями? |
|
|
|
|
||
|
РЕШЕНИЕ: |
|
|
|
210 |
||
|
а) Искомое число способов равно числу |
|
|||||
|
трехэлементных подмножеств множества из 7 |
|
|||||
|
элементов, т.е. числу сочетаний из семи элементов |
|
|||||
13

по три:
C73 = |
7! |
=1 2 3 4 5 6 7 |
=35 ; |
|
|||
|
3! 4! 1 2 3 1 2 3 4 |
|
|
б) В этом случае порядок становится существенным и выбирать нужно упорядоченные трехэлементные подмножества, их число равно числу размещений из семи элементов по три:
A73 = 7!4! =5 6 7 = 210.
ПП 1.№16. Сколько шестизначных чисел будут содержать трижды цифру 1, дважды цифру 5 и один раз цифру
9? 60
РЕШЕНИЕ:
C6 (3,2,1)= |
|
|
6! |
|
= 60 . |
|
3! |
2! 1! |
|
||||
|
|
|
||||
ПП 1.№17. Сколько различных слов можно составить из п |
|
|||||
букв, если имеется k1 букв a1, k2 букв a2 … и kr |
|
|||||
букв ar (k1 + k2+… + kr = n)? |
|
|
||||
Сколько различных слов можно составить из слова |
|
|||||
«математика»? |
|
|
|
|
|
|
РЕШЕНИЕ: |
|
|
|
|
|
|
Перенумеруем места, на которых стоят буквы, |
|
|||||
числами 1, 2, … п. Каждое слово определяется |
|
|||||
множествами: b1 {номера мест, на которых стоит |
|
|||||
буква a1}, b2 {номера мест, на которых стоит буква |
|
|||||
a2} и далее до br. Следовательно, число различных |
|
|||||
слов равно числу способов, которыми можно |
151200 |
|||||
множество А = {1,2, … n} разбить на r |
|
|||||
упорядоченных частей bi (i=1, 2, … r), то есть |
|
|||||
Cn (k1, k2, …kr). |
|
|||||
Найдем число различных слов, которое можно |
|
|||||
составить из слова «математика». |
|
|||||
В этом случае |
|
|
|
|
|
|
n =10, k1 (M ) = 2, k2 ( A) =3, k3 (T ) = 2, |
|
|||||
k4 (E) =1, k5 (И) =1, k6 (К) =1, |
|
|||||
и число слов равно |
|
|
10! |
|
|
|
C10 (2,3, 2,1,1,1) = |
|
|
=151200 . |
|
||
2!3!2! |
|
|
||||
|
|
|
|
|
||
ПП 1.№18. Каково число сочетаний костей домино? РЕШЕНИЕ:
Число сочетаний костей домино можно 28 рассматривать как сочетания с повторениями по два из семи цифр: 0, 1, 2, 3, 4, 5, 6. Число таких сочетаний равно:
14
|
|
D72 =C86 = |
8! |
= 8 7 =28 . |
||
|
|
|
||||
|
|
6! 2! |
2 |
|||
ПП 1.№19. Сколькими способами можно выбрать 6 |
||||||
одинаковых или разных пирожных в кондитерской, |
||||||
где есть 11 разных сортов? |
8008 |
|||||
РЕШЕНИЕ: |
|
|
|
|||
|
6 15 14 13 12 11 |
|
||||
D116 =C116 = |
16! |
= |
=8008 . |
|||
|
|
|||||
6!10! |
|
6 5 4 3 2 |
|
|
||
ПП 1.№20. В магазине «Все для чая » есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцами?
РЕШЕНИЕ:
Выберем чашку. В комплект с ней можно выбрать 15 любое из трех блюдец. Поэтому есть три разных комплекта, содержащих выбранную чашку.
Поэтому чашек всего 5, то число различных компонентов равно 15(15 =5 3).
ПП 1.№21. В магазине «Все для чая » есть 4 чайные ложки. |
|
|
Сколькими способами можно купить комплект из |
|
|
чашки, блюдца и ложки? |
|
|
РЕШЕНИЕ: |
|
|
Выберем любой из 15 комплектов предыдущей |
60 |
|
задачи. Его можно дополнить ложкой четырьмя |
|
|
различными способами. Поэтому общее число |
|
|
возможных комплектов равно |
|
|
60(60 =15 4 =5 3 4). |
|
|
ПП 1.№22. В магазине «Все для чая » по прежнему продается |
|
|
5 чашек, 3 блюдца и 4 чайные ложки. Сколькими |
|
|
способами можно купить два предмета с разными |
|
|
названиями? |
|
|
РЕШЕНИЕ: |
|
|
Возможны три разных случая: первый – |
47 |
|
покупаются чашка с блюдцем, второй – чашка с |
||
|
||
ложкой, третий – блюдце и ложка. В каждом из |
|
|
этих случаев легко сосчитать количество |
|
|
возможных вариантов (в первом – 15, во втором – |
|
|
20, в третьем - 12). Складывая, получаем общее |
|
|
число возможных вариантов: 47 |
|
|
ПП 1.№23. Алфавит племени Мумбо-Юбмо состоит из трех |
|
|
букв А,Б,В. Словом является любая |
|
|
последовательность, состоящая не более, чем из 4 |
120 |
|
букв. Сколько слов в языке Мумбо-Юбмо? |
||
|
||
РЕШЕНИЕ: |
|
15
Сосчитайте отдельно количество одно-, двух-, |
|
трех-, четырехбуквенные слова. |
|
3 +32 +33 +34 =120 . |
|
ПП 1.№24. Сколькими способами можно сделать трехцветный |
|
флаг с горизонтальными полосами одинаковой |
|
ширины, если имеется материя шести различных |
|
цветов? |
|
РЕШЕНИЕ: |
|
Цвет для верхней полоски флага можно выбрать |
|
шестью разными способами. После этого для |
120 |
средней полоски флага – четыре различных цвета. |
|
Таким образом, флаг можно сделать |
|
6 5 4 =120 способами. |
|
ПП 1.№25. Сколько существует трехзначных чисел, в записи |
|
которых цифры 1, 2, 3 встречаются ровно по |
|
одному разу? |
|
РЕШЕНИЕ: |
|
Будем рассуждать точно так же, как при решении |
|
задач предыдущего цикла. На первое место можно |
|
поставить любую из трех цифр, на второе – любую |
3! |
из двух оставшихся, а на третье – последнюю |
|
оставшуюся цифру. Таким образом, всего |
|
получается 3 2 1 =3 ! чисел. |
|
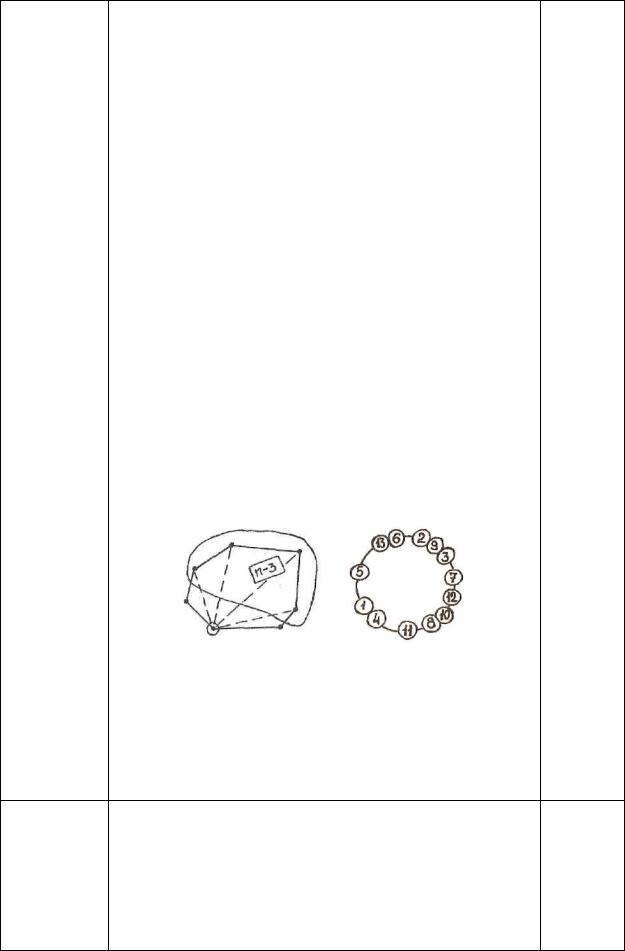
ПП 1.№27. Сколько диагоналей в n-угольнике? |
|
РЕШЕНИЕ: |
n(n −3)/ 2 |
|
|
В качестве первого конца диагонали можно взять |
|
любую из n вершин, а в качестве второго - любую |
|
из n – 3 вершин, отличных от выбранной и двух |
|
соседних с ней. При этом подсчете каждая |
|
диагональ учитывается дважды. |
|
n(n −3)/ 2 . |
|
ПП 1.№28. Сколько существует 6-значных чисел, в записи которых есть хотя бы одна четная цифра? РЕШЕНИЕ:
Вместо того, чтобы подсчитать количество 884375 требуемых 6-значных чисел, определим количество 6-зачных чисел, не обладающих нужным свойством. Так как это в точности те числа, в
16
записи которых встречаются только нечетные |
|
|
|
|
цифры, то их количество, очевидно равно |
|
|
|
|
56 =15625 . Всего 6-значных чисел 900000. Поэтому |
|
|
|
|
количество 6-значных чисел, обладающих |
|
|
|
|
указанным свойством, равно 900000 −15625 =884375 . |
|
|
|
|
ПП 1.№29. В алфавите племени Бум-Бум шесть букв. Словом |
|
|
|
|
является любая последовательность из шести букв, |
|
|
|
|
в которой есть хотя бы две одинаковых буквы. |
|
|
|
|
Сколько слов в языке племени Бум-Бум? |
|
|
|
|
РЕШЕНИЕ: |
6 |
6 |
−6 |
! |
66 −6 !. |
|
|||
ПП 1.№30. |
|
|
|
|
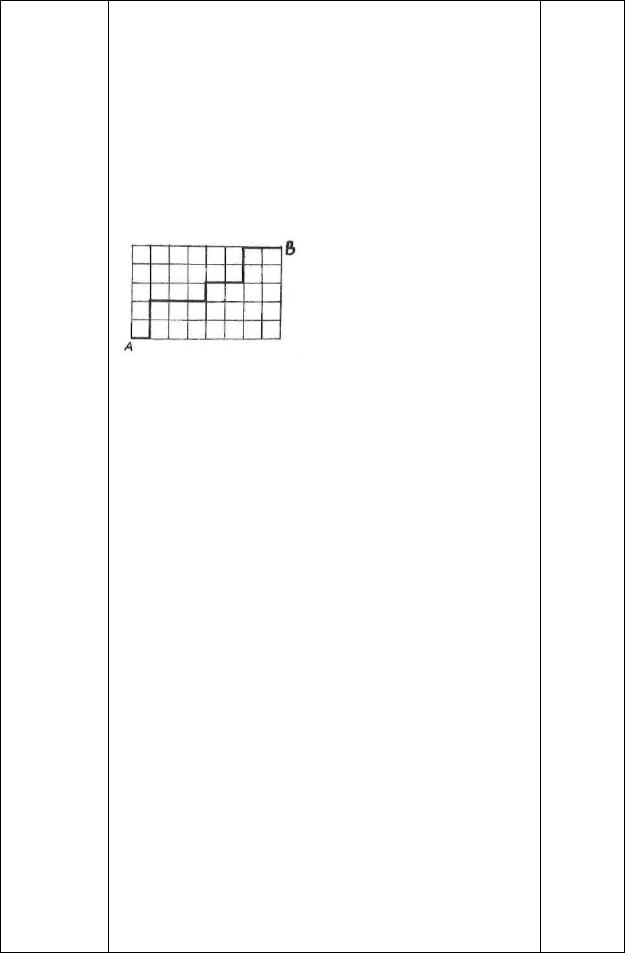
План города имеет схему, |
|
|
изображенную на рисунке. На всех улицах введено |
|
|
одностороннее движение : можно ехать только |
|
|
«вправо» или «влево». Сколько есть разных |
|
|
маршрутов, ведущих из точки А в точку В? |
|
|
РЕШЕНИЕ: |
|
|
Для удобства назовем улицей отрезок, |
|
|
изображенной сетки, соединяющий два соседних |
|
|
узла. Ясно, что каждый маршрут содержит ровно 13 |
|
|
улиц, причем 8 из них расположены по |
|
|
горизонтали, а 5 – по вертикали. Сопоставим |
C5 |
|
каждому маршруту последовательность букв Г и В |
||
13 |
||
следующим образом: при прохождении |
|
|
«горизонтальной» улицы маршрута будем |
|
|
дописывать в последовательность букву Г, а при |
|
|
прохождении «вертикальной » улицы – букву В. |
|
|
Например, маршруту, выделенного на рисунке, |
|
|
соответствует последовательность |
|
|
ГВВГГГВГГВВГГГ. Каждая последовательность |
|
|
содержит 13 букв – 8 букв Г и 5 букв В. Осталось |
|
|
вычислить количество таких последовательностей. |
|
|
Последовательность однозначно задается набором |
|
|
из 5 мест, на которых в ней стоят буквы В (или |
|
|
наоборот из 8 мест, на которых стоят буквы Г). |
|
|
Пять мест из 13 можно выбрать C135 способами. |
|
|
Поэтому число возможных последовательностей, а |
|
|
значит, и число возможны маршрутов, равно C135 . |
|
17
|
Понятно, что в прямоугольнике m ×n совершенно |
|
|
аналогичные рассуждения приводят к ответу Cmm+n |
|
|
(или, что то же самое, Cmn +n ). |
|
ПП 1.№31 |
Шесть ящиков занумерованы от 1 до 6. Сколькими |
|
|
способами можно разложить по этим ящикам 20 |
|
|
одинаковых шаров так, чтобы ни один ящик не |
|
|
оказался пустым? |
|
|
РЕШЕНИЕ: |
|
|
Выложим шары в ряд. Для определения расклада |
|
|
наших шаров по шести ящикам разделим ряд пятью |
|
|
перегородками на шесть групп: первая группа для |
C5 |
|
первого ящика, вторая – для второго и так далее. |
19 |
|
|
|
|
Таким образом, число вариантов раскладки шаров |
|
|
по ящикам равно числу способов расположения |
|
|
пяти перегородок. Перегородки могут стоять на |
|
|
любом из 19 мест (между 20 шарами – 19 |
|
|
промежутков). Поэтому число возможных |
|
|
расположений равно C195 . |
|
ПП 1.№32 |
Шесть ящиков занумерованы числами от 1 до 6 . |
|
|
Сколькими способами можно разложить по этим |
|
|
ящикам 20 одинаковых шаров (на этот раз |
|
|
некоторые ящики могут оказаться пустыми)? |
|
|
РЕШЕНИЕ: |
|
|
Рассмотрим ряд из 25 предметов: 20 одинаковых |
|
|
шаров и 5 одинаковых перегородок, |
|
|
расположенных в произвольном порядке. Каждый |
|
|
такой ряд однозначно соответствует некоторому |
|
|
способу раскладки шаров по ящикам: в первый |
|
|
ящик попадают шары, расположенные левее первой |
|
|
перегородки, во второй – расположенные между |
C255 |
|
первой и второй перегородками и т.д. (между |
|
|
какими-то перегородками шаров может и не быть). |
|
|
Поэтому число способов раскладки шаров по |
|
|
ящикам равно числу различных рядов из 20 шаров |
|
|
и 5 перегородок, т.е. равно C255 (ряд определяется |
|
|
теми пятью местами из 25, на которых стоят |
|
|
перегородки.). Отметим, что другое решение задачи |
|
|
31 можно получить так: положим сначала в каждый |
|
|
ящик по одному шару (теперь наверняка не будет |
|
|
пустых), а потом воспользуемся результатом задачи |
|
|
32. |
|
ПП 1.№33 |
Сколькими способами натуральное число n можно |
а) Cnk−−11 |
|
представить в виде суммы |
|
18
|
а) k натуральных слагаемых; |
б) Cnn+k −1 |
|
б) k неотрицательных целых слагаемых |
|
|
(представления, отличающиеся порядком |
|
|
слагаемых, считаются различными)? |
|
|
РЕШЕНИЕ: |
|
|
Представим n в виде суммы n единиц: |
|
|
n =1+1+...+1 . Назовем теперь эти n единиц |
|
|
«шарами», а k слагаемых из условия задачи – |
|
|
«ящиками». |
|
|
а) Cnk−−11 |
|
|
б) Cnn+k −1 |
|
19
