
- •5. Теория колебаний 5
- •6. Теория волновых процессов 48
- •Теория колебаний
- •Введение
- •Условия возникновения колебаний в системе. Таблица аналогий между механическими и электромагнитными колебаниями
- •Общие дифференциальные уравнения, описывающие колебания в произвольной системе
- •Механические незатухающие гармонические колебания в замкнутой системе
- •Квазиупругая сила. Математический и физический маятники. Гармонический осциллятор
- •Гармонические электромагнитные колебания в закрытом идеальном колебательном контуре
- •Сложение гармонических колебаний
- •Векторная диаграмма. Сложение гармонических колебаний одного направления и одинаковой частоты
- •СложениеNгармонических колебаний одного направления, одинаковой амплитуды и частоты, начальные фазы которых образуют арифметическую прогрессию
- •Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
- •Модулированные колебания
- •Спектральное представление различных сигналов
- •4. Наиболее общий случай: произвольная периодическая функция.
- •Затухающие колебания
- •Дифференциальное уравнение затухающих колебаний, его решение
- •Характеристики, вводимые для описания затухающих колебаний
- •Вынужденные колебания
- •Уравнения вынужденных колебаний, их решения
- •Резонансные кривые для амплитуды напряжения на конденсаторе, для амплитуды смещения в механической системе. Явление резонанса
- •Резонансные кривые для амплитуды силы тока в контуре, для амплитуды скорости материальной точки в механической системе
- •Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении колебательного контура. Фазовые резонансные кривые
- •Переменный электрический ток
- •Энергетика резонанса. Некоторые примеры проявления и применения резонанса в природе и технике
- •Нелинейные системы. Автоколебания
- •Параметрические колебания. Параметрический резонанс
- •Нормальные колебания (моды). Связанные колебательные системы
- •Теория волновых процессов
- •Волны в упругой среде
- •Характеристики волновых процессов
- •Уравнение волны. Уравнение плоской гармонической волны. Волновое уравнение. Уравнение сферической волны
- •Энергия упругой волны. Объемная плотность энергии. Вектор Умова
- •Стоячие волны. Колебания струны
- •Интерференция волн
- •Волновой пакет. Групповая скорость. Дисперсия волн
- •Звуковые волны. Скорость упругих волн в различных средах
- •Эффект Доплера для упругих и электромагнитных волн
- •Электромагнитные волны
- •Волновые уравнения для электромагнитной волны (эмв). Уравнение плоской монохроматической эмв.
- •Свойства эмв
- •Давление эмв. Опыты п.Н. Лебедева, подтверждающие электромагнитную природу света
- •Излучение эмв
- •6.2.4.1. Шкала эмв и способы возбуждения эмв
- •6.2.4.2. Излучение эмв диполем
- •Опыты с эмв
- •Ударные волны. Уединенные волны
- •Часть 4 колебания и волны
- •620002, Екатеринбург, Мира, 19
Гармонические электромагнитные колебания в закрытом идеальном колебательном контуре
В такой контур не подается внешнее напряжение (Uвнеш=0) и в нем отсутствуют потери энергии на нагревание проводников (β=0), поэтому общее дифференциальное уравнение колебаний (5.1) для такого контура запишется таким образом:
![]() ,
(5.17)
,
(5.17)
решением этого уравнения является гармоническое колебание
![]() .
(5.18)
.
(5.18)
Используя
таблицу аналогий между механическими
и электромагнитными колебаниями (табл.
5.1), можно переписать формулы (5.9) - (5.13)
для случая колебательного контура.
Таким способом можно получить зависимости
от времени силы тока I,
напряжения на конденсаторе UC,
напряжения на катушке UL,
ЭДС самоиндукции
![]() ,
энергий электрического поля конденсатораWC
и магнитного поля катушки WL,
полной энергии колебаний W
и проекций вектора напряженности
,
энергий электрического поля конденсатораWC
и магнитного поля катушки WL,
полной энергии колебаний W
и проекций вектора напряженности
![]() электрического поля конденсатора и
вектора магнитной индукции
электрического поля конденсатора и
вектора магнитной индукции
![]() магнитного
поля катушки. Итак, эти формулы имеют
следующий вид:
магнитного
поля катушки. Итак, эти формулы имеют
следующий вид:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
(5.19)
,
(5.19)
![]() ,
,
![]() ,
,![]() ,
(5.20)
,
(5.20)
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
(5.21)
,
(5.21)
![]() ,
(5.22)
,
(5.22)
![]() ,
,
![]() ,
,![]() ,
,![]() ,
(5.23)
,
(5.23)
где
d–
расстояние между обкладками плоского
конденсатора; V
– объем
катушки (она представляет собой длинный
соленоид);
![]() – магнитная постоянная.
– магнитная постоянная.
Сложение гармонических колебаний
Векторная диаграмма. Сложение гармонических колебаний одного направления и одинаковой частоты
Возьмем
ось
![]() .
Из начала оси (точкаО)
отложим вектор
.
Из начала оси (точкаО)
отложим вектор
![]() под углом
под углом![]() к оси
к оси![]() (рис. 5.6). Если этот вектор вращать вокруг
точки
(рис. 5.6). Если этот вектор вращать вокруг
точки![]() с угловой скоростью
с угловой скоростью![]() ,
то тогда проекция вектора
,
то тогда проекция вектора![]() на ось
на ось![]() будет изменяться по гармоническому
закону
будет изменяться по гармоническому
закону
![]() ,
,
![]() .
.
Такое
построение называют векторной
диаграммой.
Гармоническое колебание на векторной
диаграмме совершает проекция вектора
![]() на ось
на ось![]() .
Причем циклическая частота
.
Причем циклическая частота![]() колебаний будет равна по модулю угловой
скорости
колебаний будет равна по модулю угловой
скорости![]() вращения вектора
вращения вектора![]() .
.
 Пусть
тело (м.т.) одновременно участвует в двух
гармонических колебаниях одинаковой
частоты, происходящих в одном направлении,
причем амплитуды и начальные фазы
колебаний различны (
Пусть
тело (м.т.) одновременно участвует в двух
гармонических колебаниях одинаковой
частоты, происходящих в одном направлении,
причем амплитуды и начальные фазы
колебаний различны (![]() ,
,![]() ):
):
![]() ,
,![]() .
(5.24)
.
(5.24)
Результирующее
движение, равное сумме колебаний
![]() и
и![]() ,
будет также гармоническим колебанием
той же циклической частоты
,
будет также гармоническим колебанием
той же циклической частоты![]()
Рис. 5.6
![]() .
.
Необходимо
найти амплитуду и начальную фазу
результирующего колебания. Это можно
сделать с помощью векторной диаграммы.
Для этого проведем из точки О
векторы с амплитудами А1
и А2
под углами
![]() и
и![]() к оси
к оси![]() и приведем их во вращение с угловой
скоростью
и приведем их во вращение с угловой
скоростью![]() (рис. 5.7).
(рис. 5.7).
Проекции
векторов
![]() и
и![]() на ось
на ось![]() при этом совершают гармонические
колебания в соответствии с уравнениями
(5.24). Результирующее колебание будет
изображаться проекцией на ось
при этом совершают гармонические
колебания в соответствии с уравнениями
(5.24). Результирующее колебание будет
изображаться проекцией на ось![]() вектора
вектора![]() ,
полученного из векторов
,
полученного из векторов![]() и
и![]() по правилу параллелограмма. Из построения
на Рис. 5.7 следует, что квадрат амплитуды
вектора
по правилу параллелограмма. Из построения
на Рис. 5.7 следует, что квадрат амплитуды
вектора![]() можно найти по теореме косинусов из
треугольника ΔОА2А:
можно найти по теореме косинусов из
треугольника ΔОА2А:
![]() ,
,![]()
![]() .
(5.25)
.
(5.25)
Из
треугольников ΔОА1В
и ΔОАС
для начальной фазы
![]() результирующего колебания можно найти
следующее выражение:
результирующего колебания можно найти
следующее выражение:
![]() .
(5.26)
.
(5.26)
Рассмотрим частные случаи сложения колебаний.

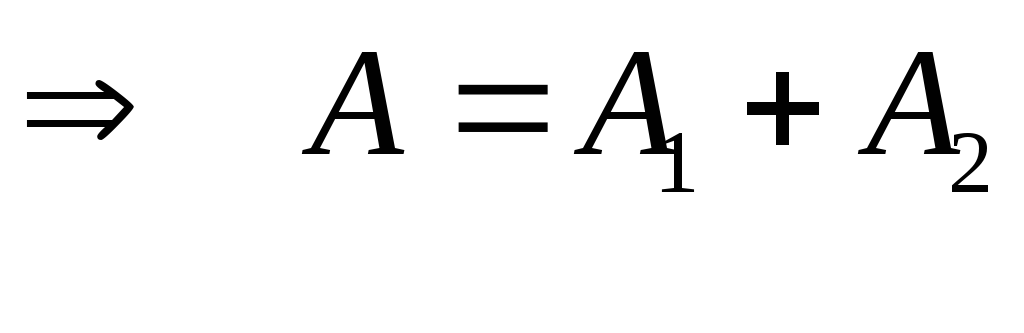 ,
(5.27)
,
(5.27)
т.е. если разность фаз складываемых колебаний равна четному числу π, то колебания максимально усиливают друг друга.

 ,
(5.28)
,
(5.28)
 т.е.,
если разность
фаз складываемых колебаний равна
нечетному числу π, то колебания
максимально ослабляют друг друга.
т.е.,
если разность
фаз складываемых колебаний равна
нечетному числу π, то колебания
максимально ослабляют друг друга.
3.
![]()
![]() .
.
На
рис. 5.8 приведены результаты сложения
гармонических колебаний в рассмотренных
выше случаях 1,2 и 3, при условии, что
![]() =0
иА1>
А2.
=0
иА1>
А2.
Рис. 5.7
Полученные условия максимального усиления (5.27) и ослабления (5.28) колебаний при сложении колебаний одного направления и одинаковой частоты
будут использованы при изучении интерференции когерентных волн.
