
- •5. Теория колебаний 5
- •6. Теория волновых процессов 48
- •Теория колебаний
- •Введение
- •Условия возникновения колебаний в системе. Таблица аналогий между механическими и электромагнитными колебаниями
- •Общие дифференциальные уравнения, описывающие колебания в произвольной системе
- •Механические незатухающие гармонические колебания в замкнутой системе
- •Квазиупругая сила. Математический и физический маятники. Гармонический осциллятор
- •Гармонические электромагнитные колебания в закрытом идеальном колебательном контуре
- •Сложение гармонических колебаний
- •Векторная диаграмма. Сложение гармонических колебаний одного направления и одинаковой частоты
- •СложениеNгармонических колебаний одного направления, одинаковой амплитуды и частоты, начальные фазы которых образуют арифметическую прогрессию
- •Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
- •Модулированные колебания
- •Спектральное представление различных сигналов
- •4. Наиболее общий случай: произвольная периодическая функция.
- •Затухающие колебания
- •Дифференциальное уравнение затухающих колебаний, его решение
- •Характеристики, вводимые для описания затухающих колебаний
- •Вынужденные колебания
- •Уравнения вынужденных колебаний, их решения
- •Резонансные кривые для амплитуды напряжения на конденсаторе, для амплитуды смещения в механической системе. Явление резонанса
- •Резонансные кривые для амплитуды силы тока в контуре, для амплитуды скорости материальной точки в механической системе
- •Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении колебательного контура. Фазовые резонансные кривые
- •Переменный электрический ток
- •Энергетика резонанса. Некоторые примеры проявления и применения резонанса в природе и технике
- •Нелинейные системы. Автоколебания
- •Параметрические колебания. Параметрический резонанс
- •Нормальные колебания (моды). Связанные колебательные системы
- •Теория волновых процессов
- •Волны в упругой среде
- •Характеристики волновых процессов
- •Уравнение волны. Уравнение плоской гармонической волны. Волновое уравнение. Уравнение сферической волны
- •Энергия упругой волны. Объемная плотность энергии. Вектор Умова
- •Стоячие волны. Колебания струны
- •Интерференция волн
- •Волновой пакет. Групповая скорость. Дисперсия волн
- •Звуковые волны. Скорость упругих волн в различных средах
- •Эффект Доплера для упругих и электромагнитных волн
- •Электромагнитные волны
- •Волновые уравнения для электромагнитной волны (эмв). Уравнение плоской монохроматической эмв.
- •Свойства эмв
- •Давление эмв. Опыты п.Н. Лебедева, подтверждающие электромагнитную природу света
- •Излучение эмв
- •6.2.4.1. Шкала эмв и способы возбуждения эмв
- •6.2.4.2. Излучение эмв диполем
- •Опыты с эмв
- •Ударные волны. Уединенные волны
- •Часть 4 колебания и волны
- •620002, Екатеринбург, Мира, 19
Эффект Доплера для упругих и электромагнитных волн
Под эффектом Доплера понимают изменение частоты, регистрируемой приемником волны, связанное с движением источника и приемника. Впервые теоретически этот эффект в акустике и оптике был обоснован австрийским физиком К. Доплером в 1842 г.
Рассмотрим
вывод формулы, определяющей частоту
упругой волны, воспринимаемой приемником,
на примере двух частных случаев. 1.
В среде находятся неподвижные источник
и приемник звуковых волн.
Испускаемые источником волны частоты
![]() и длины волны
и длины волны ![]() ,
двигаясь со скоростью
,
двигаясь со скоростью ![]() ,
достигают приемника и создают в нем
колебания такой же частоты
,
достигают приемника и создают в нем
колебания такой же частоты ![]() (рис. 6.11,а). 2.
Источник и испускаемая им волна движутся
вдоль оси Ох. Приемник движется к ним
навстречу.
Отметим, что скорость волны
(рис. 6.11,а). 2.
Источник и испускаемая им волна движутся
вдоль оси Ох. Приемник движется к ним
навстречу.
Отметим, что скорость волны ![]() зависит только от свойств среды и не
зависит от движения приемника и источника.
Поэтому движение источника при постоянной
частоте
зависит только от свойств среды и не
зависит от движения приемника и источника.
Поэтому движение источника при постоянной
частоте ![]() излучаемых им колебаний приведет к
изменению только длины волны. Действительно,
источник за период колебаний
излучаемых им колебаний приведет к
изменению только длины волны. Действительно,
источник за период колебаний ![]() пройдет расстояние
пройдет расстояние ![]() ,
а по закону сложения скоростей волна
отойдет от
источника
на расстояние
,
а по закону сложения скоростей волна
отойдет от
источника
на расстояние
![]() ,
и поэтому ее длина волны
,
и поэтому ее длина волны ![]() будет меньше
будет меньше
![]() (рис.6.11,б).
(рис.6.11,б).
По
отношению к приемнику волна в соответствии
с законом сложения скоростей будет
двигаться со скоростью
![]() и для неизменной длины волны
и для неизменной длины волны
![]() частота
частота
![]() колебаний, воспринимаемых источником,
изменится и будет равна
колебаний, воспринимаемых источником,
изменится и будет равна
![]() .
.
Если
источник и приемник будут удаляться
друг от друга, то тогда в формуле для
частоты ![]() нужно изменить знаки. Следовательно,
единая формула для частоты колебаний,
воспринимаемой приемником, при движении
источника и приемника по одной прямой,
будет выглядеть следующим образом:
нужно изменить знаки. Следовательно,
единая формула для частоты колебаний,
воспринимаемой приемником, при движении
источника и приемника по одной прямой,
будет выглядеть следующим образом:
![]() .
(6.36)
.
(6.36)
Из этой формулы следует, что для наблюдателя, находящегося, например на станции, частота звукового сигнала приближающегося поезда (υПР=0, υИСТ>0)
будет больше, а при удалении от станции меньше. Если, например, взять скорость звука υ=340 м/с, скорость поезда υ=72 км/ч и частоту звукового сигнала ν0=1000 Гц (такая частота хорошо воспринимается человеческим ухом, причем ухо различает звуковые волны с разностью частот, большей 10 Гц), тогда частота сигнала, воспринимаемого ухом будет изменяться в пределах

Рис. 6.11
![]() =
=![]()
Если
источник и приемник движутся со
скоростями, направленными под углом к
соединяющей их прямой, то тогда для
расчета частоты
![]() ,
воспринимаемой приемником, нужно брать
проекции их скоростей на эту прямую
(рис. 6.11,в):
,
воспринимаемой приемником, нужно брать
проекции их скоростей на эту прямую
(рис. 6.11,в):
![]() .
(6.37)
.
(6.37)
Эффект Доплера наблюдается и для электромагнитных волн. Но в отличие от
упругих волн, ЭМВ могут распространяться в отсутствии среды, в вакууме. Следовательно, для ЭМВ не имеет значения скорость движения источника и приемника относительно среды. Для ЭМВ необходимо рассматривать относительную скорость движения источника и приемника, учитывать при этом преобразования Лоренца и замедление хода времени в движущейся системе отсчета.
Рассмотрим продольный эффект Доплера. Выведем формулу для частоты ЭМВ, фиксируемой приемником, в частном случае – источник и приемник движутся навстречу друг другу в направлении соединяющей их прямой. Пусть имеются две И.С.О. – неподвижная И.С.О. К (в ней находится неподвижный приемник ЭМВ) и движущаяся относительно нее вдоль совпадающих осей координат Ох и Ох′ И.С.О. К′ (в ней находится неподвижный источник ЭМВ) (рис. 6.12,а).

Рис. 6.12
Рассмотрим, что наблюдается в И.С.О. К и К'.
1.
И.С.О.
К′.
Источник ЭМВ неподвижен и находится в
начале оси координат Ох′
(рис. 6.12,а). Он излучает в И.С.О. К′
ЭМВ с периодом ![]() ,
частоты
,
частоты ![]() и длины волны
и длины волны ![]() .
.
Приемник
движется, но его движение не влияет на
изменение частоты принимаемого сигнала.
Это связано с тем, что, согласно второму
постулату С.Т.О., скорость ЭМВ относительно
приемника будет всегда равна с,
и поэтому частота принимаемой приемником
волны в И.С.О. К'
будет также равна
![]() ,
,
2.
И.С.О. К.
Приемник ЭМВ неподвижен, а источник
ЭМВ движется в направлении оси Ох
со скоростью
![]() .
Поэтому для источника необходимо учесть
релятивистский эффект замедления
времени. Это означает, что период волны,
излучаемой источником в этой инерциальной
системе отсчета, будет больше периода
волны в И.С.О.
.
Поэтому для источника необходимо учесть
релятивистский эффект замедления
времени. Это означает, что период волны,
излучаемой источником в этой инерциальной
системе отсчета, будет больше периода
волны в И.С.О. ![]() (
(![]() ).
).
Для
длины волны ![]() ,
излучаемой источником в направлении
приемника, можно записать
,
излучаемой источником в направлении
приемника, можно записать
![]() .
.
Это
выражение позволяет для периода Т
и частоты ![]() воспринимаемой приемником ЭМВ в И.С.О.
К,
записать следующие формулы:
воспринимаемой приемником ЭМВ в И.С.О.
К,
записать следующие формулы:
![]()
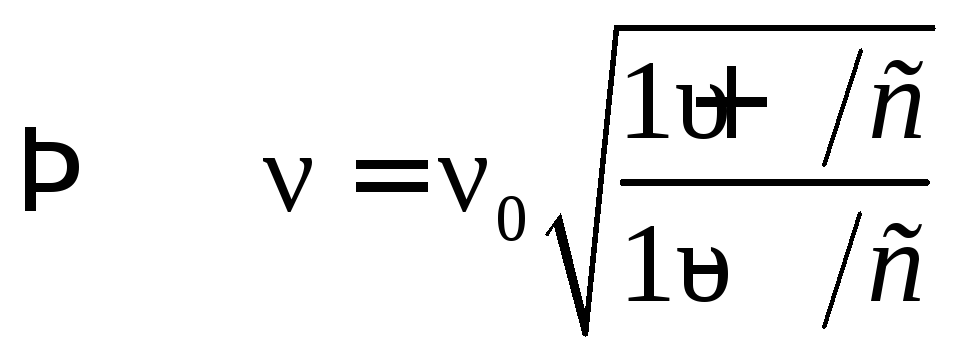 ,
(6.38)
,
(6.38)
где учтено, что скорость ЭМВ относительно приемника в И.С.О. К равна с.
В случае удаления источника и приемника необходимо в формуле (6.38) изменить знаки. При этом фиксируемая приемником частота излучения будет уменьшаться по сравнению с частотой волны, излучаемой источником, т.е. наблюдается красное смещение спектра видимого света.
Как видно, в выражение (6.38) не входит скорость источника и приемника по отдельности, входит только скорость их относительного движения.
Для
ЭМВ также наблюдается поперечный
эффект Доплера,
который связан с эффектом замедления
времени в движущейся инерциальной
системе отсчета. Возьмем момент времени,
когда скорость источника ЭМВ будет
перпендикулярна линии наблюдения (рис.
6.12,б), тогда движение источника к приемнику
не происходит и поэтому длина излучаемой
им волны не изменяется (![]() ).
Остается только релятивистский эффект
замедления времени
).
Остается только релятивистский эффект
замедления времени
![]() ,
,
![]() .
(6.39)
.
(6.39)
Для
поперечного эффекта Доплера изменение
частоты будет существенно меньше, чем
для продольного эффекта Доплера.
Действительно, отношение частот,
найденных по формулам (6.38) и (6.39), для
продольного и поперечного эффектов
будет значительно меньше единицы: ![]() .
.
Поперечный эффект Доплера был подтвержден экспериментально, что еще раз доказало справедливость специальной теории относительности.
Приведенные
здесь доводы в пользу формулы (6.39) не
претендуют на строгость, но они дают
правильный результат. В общем случае,
для произвольного угла ![]() между линией наблюдения и скоростью
движения источника
между линией наблюдения и скоростью
движения источника ![]() ,
можно записать следующую формулу
,
можно записать следующую формулу
 ,
(6.40) где угол
,
(6.40) где угол
![]() - это угол между линией наблюдения и
скоростью движения источника см. (рис.
6.12, б).
- это угол между линией наблюдения и
скоростью движения источника см. (рис.
6.12, б).
Поперечный эффект Доплера отсутствует для упругих волн в среде. Это связано с тем, что, для определения частоты волны, воспринимаемой приемником, берутся проекции скоростей на прямую, соединяющую источник и приемник см. (рис. 6.11,в), а замедление времени для упругих волн отсутствует.
Эффект Доплера находит широкое практическое применение, например для измерения скоростей движения звезд, галактик по доплеровскому (красному) смещению линий в спектрах их излучения; для определения скоростей движущихся целей в радиолокации и гидролокации; для измерения температуры тел по доплеровскому уширению линий излучения атомов и молекул и т.д.
