Параметрические колебания. Параметрический резонанс
Параметрические колебания – это колебания, происходящие в системе за счет периодического изменения тех параметров системы, которые определяют величину запасенной колебательной энергии. Так, например, можно возбудить параметрические колебания в колебательном контуре за счет периодического изменения электроемкости конденсатора или индуктивности катушки, параметрические колебания маятника за счет изменения длины его нити или массы груза.
Если
обозначить через 
частоту собственных незатухающих
колебаний в системе, то параметрическое
возбуждение колебаний в системе наступает
в тех случаях, когда частота периодического
изменения 
параметра системы будет удовлетворять
условию
.
(5.91)
При
таких значениях частоты 
в системе будут возбуждаться собственные
колебания системы на частоте 
.
Наиболее благоприятной для возбуждения
колебаний является частота 
,
равная 
,
так как на этой частоте совершает
колебания энергия системы (потенциальная
и кинетическая энергии, энергия
электрического поля конденсатора и
магнитного поля катушки индуктивности).
При такой частоте колебания в системе
будут наиболее интенсивными.
Поясним
это на примере периодического изменения
электроемкости конденсатора колебательного
контура. Пусть момент времени
,
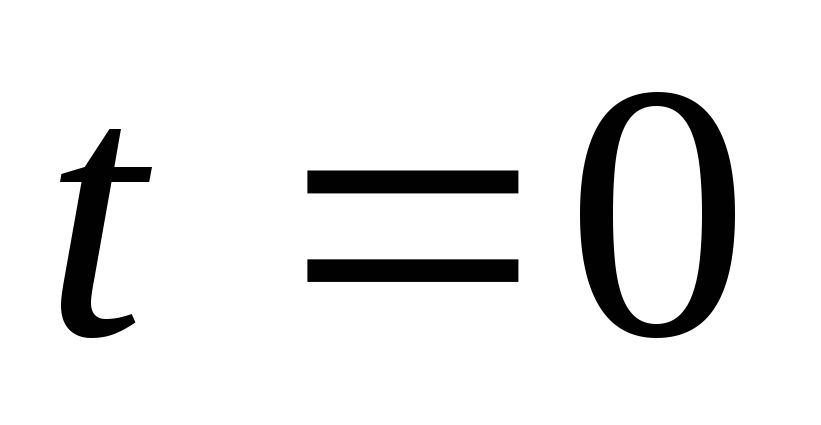заряд на обкладках конденсатора будет
максимальным и в этот момент времени
скачком (за время, малое по сравнению с
периодом собственных колебаний)
раздвигаются пластины конденсатора.
Тогда энергия электрического поля
конденсатора будет увеличиваться, в
контур поступает энергия:
.
Через четверть периода колебаний (
)
конденсатор будет разряжен (
),
вся энергия контура будет сосредоточена
в катушке в виде энергии магнитного
поля. Поэтому сближение обкладок
конденсатора в этот момент времени не
приводит к отводу энергии колебаний из
контура.
Таким образом, за один период колебаний в контур два раза подводится энергия. Аналогичные процессы протекают при периодическом изменении индуктивности катушки контура.
Возникновение
параметрических колебаний возможно и
при отсутствии энергии колебаний в
системе, это объясняется следующим
образом. В любой колебательной системе
вследствие воздействия на нее различных
случайных факторов всегда существуют
малые отклонения различных физических
величин от их средних значений (их
называют флуктуациями). Спектр частот
таких флуктуаций будет непрерывным с
малыми амплитудами отдельных гармоник
(для напряжения на конденсаторе или
индуктивности они составляют значения
порядка микровольта). Периодическое
изменение параметра системы на частоте,
кратной 
,
приводит к тому, что амплитуда гармоники
с частотой 
будет все время увеличиваться за счет
подвода энергии в систему извне и в
системе возникают незатухающие колебания
с большой амплитудой.
Такое возбуждение колебаний в системе получило название параметрического резонанса.
Нарастание
амплитуды колебаний при параметрическом
резонансе ограничивается при достаточно
больших амплитудах нелинейными эффектами.
К ним можно отнести, например, возникновение
зависимости активного сопротивления
R
от амплитуды силы тока в контуре (это
приводит к увеличению потерь энергии
на выделение джоулевой теплоты) или
зависимости электроемкости конденсатора
от напряжения (это приводит к изменению
частоты 
собственных колебаний и в результате
к увеличению расстройки (
)
между частотами
и 
).
Равновесное значение амплитуды колебаний
наступает тогда, когда параметрическая
накачка энергии в среднем за период
компенсируется джоулевыми потерями.
Явление параметрического резонанса используется при работе малошумящих параметрических усилителей СВЧ-диапазона, в которых применяются
параметрические полупроводниковые диоды с управляемой емкостью р-n перехода.
Примером
параметрического резонанса в механической
системе является маятник в виде груза
массы m
, подвешенного на нити, длину
которой можно изменять (рис. 5.26,а).
Если
уменьшать длину в нижнем положении и
увеличивать в крайних положениях, то
работа внешней силы за один период
колебаний будет положительной и амплитуда
колебаний будет возрастать. Траектория
движения груза при таких колебаниях
показана на рис. 5.26,б
Раскачка качелей также обусловлена параметричес-
ким резонансом, когда эффективная длина маятника (положение центра тяжести) изменяется при приседаниях и вставаниях человека.
Рис. 5.26