Математика

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина

Кафедра высшей математики

МАТЕМАТИКА

Часть 2. ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Научный редактор – доц., канд. физ.-мат. наук Л.П. Мохрачева

Рекомендовано Уральским отделением Учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов специальностей направления 6533500

«Строительство» всех форм обучения

Екатеринбург

УрФУ

2010

3

Базис, состоящий из единичных взаимно перпендикулярных векторов (ортов), называется ортонормированным (ОНБ).

Базисом B на прямой будем называть любой ненулевой вектор этой прямой. Если a – произвольный вектор какой-либо прямой, то любой вектор на

этой прямой b может быть записан в виде b =αa .

Базисом B на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определен-

ном порядке. Если a и b – произвольные неколлинеарные векторы на плоскости, то любой вектор на этой плоскости

с может быть записан в виде с =αa + βb ={α,β} .

Каждый вектор пространства может быть разложен по базису в пространстве.

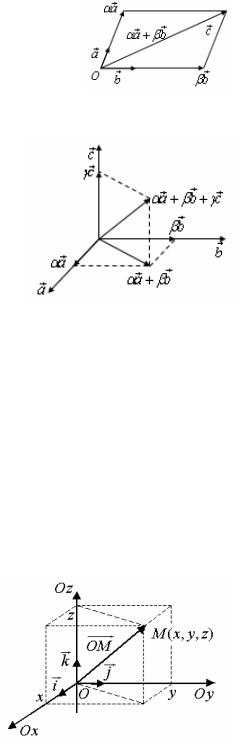
Если a , b , с – три некомпланарных вектора в пространстве, то любой вектор d может быть записан в виде d =αa + βb +γc ={α,β,γ}.

Геометрически вектор d представляет собой пространственную диагональ параллелепипеда, по-

строенного на векторах a , b и с .

Числа α, β, γ называются координатами вектора в соответствующем базисе.

Теорема. Разложение вектора по базису единственно.

Декартова прямоугольная система координат

Декартова система координат в пространстве определяется заданием точки О – начала координат и базисных векторов i , j , k (трех взаимно перпендикулярных векторов единичной длины).

Вектор OM , идущий из начала координат в точку M (x,y,z), называется радиус-вектором

точки M .

6

Два вектора равны тогда и только тогда, когда равны их соответствующие координаты в одном и том же базисе.

Линейные операции над векторами сводятся к линейным операциям над их координатами: a +b ={ax +bx , ay +by , az +bz}, αa ={αax ,αay ,αaz}.

Проекция вектора на ось

Осью называется прямая с лежащим на ней единичным вектором e (ортом), задающим положительное направление на прямой.

Проекцией прe a вектора a на ось называется направленный отрезок на оси, алгебраическое значение которого равно скалярному произведению (a e ).

Для вектора a = AB проекция на прямую OL равна числу aOL = прOL a = ± A ' B ' = a cos ϕ .

Проекции обладают свойствами:

1)прe (a +b )= прe (a)+прe (b );

2)λ прe a =прe λa .

ной длины в направлении вектора a .

7

1.4. Скалярное произведение векторов

Скалярным произведением (a b ) ненулевых векторов a иb называется

число, равное произведению длин этих векторов на косинус угла ϕ между ними:

(a b )= a b cosϕ , ϕ [0,π].

Скалярное произведение обладает свойствами:

1.(a b )= (b a);

2.((αa ) b )=α (a b );

3.((a +b ) c )= (a c )+(b c );

4.(a a )> 0 , если a ≠ 0 ;

5.(a a)= 0 , если или a = 0 , или b = 0 , или a b .

Выражение скалярного произведения векторов в декартовых координатах

Теорема. Если два вектора a и b определены своими декартовыми прямоугольными координатами a ={ax , ay , az }, b ={bx ,by ,bz }, то скалярное произве-

дение этих векторов равно сумме произведений их соответствующих координат, то есть

(a b )= axbx +ayby +azbz .

Доказательство. (a b )= ((axi +ay j + az k ) (bxi +by j +bz k ))= axbx ( i i ) +

+axby (i j )+axbz (i k )+aybx (j i )+ayby (j j )+aybz (j k )+azbx (k i )+azby (k j )+azbz (k k ).

(i j )= (i k )= (j i )= (j k )= (k i )= (k j )=1 1 cos 90o = 0;

(a b )= axbx +ayby +azbz .

8

Геометрические приложения скалярного произведения векторов в декартовой системе координат

4. Для направляющих косинусов справедливо соотношение cos2α +cos2 β +cos2γ =1.

1.5.Векторное произведение векторов

Впространстве различают правые и левые тройки векторов. Упорядо-

ченная тройка некомпланарных векторов a ,b , c , приведенных к одному на-

чалу, называется правой, если из конца третьего вектора c кратчайший пово-

рот первого вектора a ко второму b виден совершаемым против часовой стрелки. В противном случае тройка называется левой.

a2

a a

правая левая

Тройку векторов базиса i , j , k принято считать правой.

При перестановке местами двух соседних векторов ориентация тройки

меняется.

Если тройки abc, cab, bca - правые, то acb, cba, bac - левые.

При круговой (циклической) перестановке векторов ориентация тройки

не меняется.

9