МАТЕМАТИКА Ч1.7,8 ФормулыБибл

7. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ

Определители второго и третьего порядка

порядка.

Определителем квадратной матрицы A второго порядка называется число, рав-

третьего порядка.

Определителем квадратной матрицы А третьего порядка называется число, равное

a11a22 a33 a12 a23 a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32 .

Правило треугольников:

Знаки (+) и (–) соответствуют знакам определенных слагаемых, входящих в определитель. Число всех элементов определителя 3-го порядка равно 3 3 = 9.

Свойства определителей

1 ) . Определитель квадратной матрицы А не меняется при транспонировании:

AT A .

2). При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак. Например

3 ) . Определитель, содержащий две одинаковые строки (столбца), равен нулю. 4). Умножение всех элементов некоторой строки (столбца) определителя |A| на

94

число k равносильно умножению определителя на это число. Например

5). Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю

6). Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.

7). Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей. Например

8 ) . Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится. Например

9). Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения (определены ниже):

10). Определитель произведения матриц А и В (определено ниже) равен произведению их определителей:

A B A B

Определители n–го порядка

Число всех слагаемых в определителе n -го порядка равно n n n 1 n 2 3 2 1.

Минором Мij элемента аij ( иначе – дополнительный минор элемента аij) определителя n-го порядка называется определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых

95

стоит элемент aij.

.

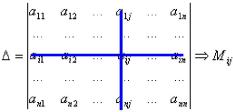Алгебраическим дополнением Аij элемента аij называется его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Aij ( 1)i j Mij .

Для определителей n -го порядка имеют место все перечисленные выше свойства определителей.

Методы вычисления определителей n–го порядка

Метод понижения порядка (разложение определителя по элементам строки или столбца)

Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения.

Метод сведения к треугольному виду

Используя свойства 1) – 9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.

Матрицы. Виды матриц

Матрицей размерности m n называется прямоугольная таблица чисел aij :

96

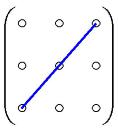, - главная и побочная диагонали.

Операции над матрицами

Транспонирование. Если матрица A имеет размерность m n , транспони-

рованная матрица AT B имеет размерность n m и элементы транспониро-

Равенство. Если A и B матрицы одинаковой размерности, то A B aij bij .

Сумма. C A B cij aij bij ; A B B A (слагаемые одной размерности).

Умножение на число. B A bij aij ;

( )A ( A) , (A B) A B , 0 A O; 1 A A.

Иначе: элемент, стоящий на пересечении i –й строки и j –го столбца матрицы произведения cij , равен сумме произведений элементов i –й строки матрицы А

на соответствующие элементы j –го столбца матрицы В.

97

Число столбцов первой матрицы равно числу строк второй матрицы.

В общем случае A B B A ; если A B B A, то матрицы перестановочные (коммутирующие).

Свойства:

1)A B C A B C .

2)A B C A C B C .

3)A B C A B A C .

4)A E E A A.

5)A O O A O .

6)A B T BT AT .

(Свойства 4) и 5) справедливы только для квадратной матрицы А).

Обратная матрица

Квадратная матрица A n –го порядка называется вырожденной, если определитель этой матрицы равен нулю, A 0 , и невырожденной, если A 0 .

Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение: A A 1 A 1 A E .

Если матрица A не вырождена, то существует, и притом единственная, обрат-

рица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).

Свойства обратной матрицы:

1) A 1 1 A .

2 A 1 1 A 1 .

3A B 1 B 1 A 1 .

4A 1 T AT 1 .

Алгоритм нахождения обратной матрицы с помощью присоединенной матрицы:

1.Находим det A , проверяем det A 0 .

2.Находим Mij - все миноры матрицы A .

3.Определяем Aij ( 1)i j Mij .

4.Строим матрицу алгебраических дополнений AV Aij и транспонируем:

98

AV T Aji .

5.Делим каждый элемент матрицы на det A : A 1 det1 A AV T .

К элементарным преобразованиям строк (столбцов) матрицы относятся следующие:

перестановка строк (столбцов);

умножение строки (столбца) на число 0;

прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на некоторое число;

Алгоритм нахождения обратной матрицы с помощью элементарных преобразований строк

Для данной матрицы A n -го порядка строим прямоугольную матрицу

A A E размера n 2n , приписывая к A справа единичную матрицу. Да-

лее, используя элементарные преобразования строк, приводим матрицу A к

виду E B , что всегда возможно, если матрица невырождена. Тогда B A 1 .

Решение матричных уравнений

Равенство, содержащее неизвестную матрицу X и известные матрицы A, B, C,…, называется матричным уравнением относительно матрицы X, например, A X B .

Простейшие типы матричных уравнений:

Ранг матрицы

Пусть в матрице A размерности m n выбраны k строк и k столбцов,

причем k min m,n . Тогда элементы, стоящие на пересечении выбранных

строк и столбцов, образуют квадратную матрицу k -го порядка. Определитель Mk этой матрицы называется минором k -го порядка матрицы A.

Рангом матрицы A называется число, равное максимальному порядку r отличных от нуля миноров Mk этой матрицы:

r r A rang A.

Матрицы одинаковой размерности называются эквивалентными, что обозна-

99

чается A B , если r A r B .

Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.

Метод окаймляющих миноров

Пусть в матрице A элемент aij 0, тогда M1 0 и rangA 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например,j 1 -го столбца и i 1 -й строки), получаем минор 2-го порядка:

Если M2 0 , то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка. Если все миноры второго порядка равны нулю, то rangA 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то rangA 2 .

Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr 0 , но все Mr 1 0. Тогда rangA r .

Метод элементарных преобразований

Элементарные преобразования матрицы не меняют ее ранга.

Кэлементарным преобразованиям матрицы относятся следующие:

перестановка строк (столбцов);

умножение строки (столбца) на число 0;

прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число;

Кроме того, ранг матрицы не меняется при транспонировании матрицы и при отбрасывании нулевой строки (столбца) .

Для определения ранга матрицы A методом элементарных преобразований следует:

1.Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.

2.Все элементы первого столбца, кроме a11 , обратить в ноль с помощью

элементарных преобразований строк:

3.Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 0. Повторить операцию 2) со вторым столбцом: во втором столбце

100

все элементы, кроме a12 и a22 , обратить в ноль.

Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системы m линейных уравнений с n неизвестными. Определения

Рассмотрим систему линейных уравнений вида

a11x1 a12 x2 . . . a1n xn b1,

Решением системы линейных уравнений (1) называется такое множество чисел x1 , x2 ,..., xn , при подстановке которых в каждое из уравнений системы по-

Система линейных уравнений (1) называется неоднородной, если матрица B не является нуль матрицей O , и называется однородной, если B O . Система линейных уравнений называется совместной, если она имеет решения, и называется несовместной - в противном случае. Система называется определенной, если она имеет единственное решение, и называется неопределенной, если она имеет бесконечное множество решений.

Системы n линейных уравнений с n неизвестными

В этом случае матрица A – квадратная. Определитель матрицы A называется главным определителем системы линейных уравнений и обозначается сим-

101

волом .

Метод Крамера решения систем n линейных уравнений с n неизвестными

Правило Крамера. Если главный определитель системы линейных уравнений не равен нулю, то система совместна и определена, причем единственное решение вычисляется по формулам Крамера:

Здесь i - определители, получаемые из главного определителя системы заменой i -го столбца на столбец свободных членов.

Системы m линейных уравнений с n неизвестными

системы.

Теорема Кронекера Капелли. Для того чтобы система линейных уравнений (1) была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы системы, rang( ) rang .

Если rang( ) rang то система заведомо не имеет решений. Eсли rang( ) rang , то возможны два случая:

1) rang A n (числу неизвестных) решение единственно и может быть по-

лучено по формулам Крамера;

2) rang A n решений бесконечно много.

Схема отыскания решения системы m линейных уравнений с n неизвестными

Пусть rang( ) rang r и rang A n . Тогда любой отличный от

нуля минор, составленный из коэффициентов матрицы порядка r , можно выбрать в качестве базисного, при этом неизвестные xi , имеющие своими коэффициентами элементы базисного минора, называются базисными неизвестными, а остальные неизвестных свободными. Свободные неизвестные могут принимать произвольные значения. Пусть, для определенности, базисный минор располагается в первых r строках и r столбцах матрицы A системы:

102

неизвестные.

Перенесем свободные неизвестные в правую часть уравнений системы:

Система (2) равносильна исходной системе (1); ее решение может быть найдено или по формулам Крамера, или матричным способом. При этом базисные

Поскольку свободные неизвестные могут принимать произвольные числовые значения, то исходная система имеет бесконечно много решений.

Метод Гаусса решения систем линейных уравнений

Элементарными преобразованиями системы являются следующие:

1)перемена местами двух любых уравнений системы;

2)умножение любого уравнения системы на произвольное число k 0;

3)прибавление к одному уравнению системы другого уравнения, умноженного на произвольное число k 0.

Элементарным преобразованиям уравнений соответствуют элементарные

103