Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matan__teoria

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.78 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

	n
∫	f (P)dσ = lim ∑ f (Pk ) σk .
(σ )	d→0 k=1

Удобно разбить поверхность (σ ) на ячейки координатными линиями

лим одну из таких ячеек (рис. 51). Рассмотрим радиус(векторы

точек

P, P ,

= r (u,v), r

= r (u + u,v), r

= r

(u,v + v).

Тогда

= r

− r

= r (u + u,v)− r (u,v) =

r ≈ r ′ u,

− r

= r (u,v + v)− r

(u,v) =

r ≈ r ′

и площадь ячейки σ

≈

u v.

× PP

′× r ′

По аналогии с этим элемент площади поверхности

d σ =

ru′ × rv′

dudv

lu , lv . Выде(

P1		lu
•		lu
P
P2
rP2	l	v
		v
Рис.51

(7.34)

Можно показать (строгое доказательство опускаем), что

		∫	f (P)dσ = ∫ f (x, y, z)dσ = ∫∫ f (x(u,v), y(u,v), z(u,v))			ru′×rv′		du dv.	(7.35)
		(σ)	(σ)	(S)
		(σ)	(σ)	(S)

Итак, получили следующее правило:

	Для вычисления поверхностного интеграла ∫ f (P)dσ = ∫ f (x, y, z)dσ следует
				(σ)		(σ)
	1) в подынтегральной функции подставить вместо				x, y, z		их значения на
	поверхности (σ ), т.е.			x = x(u,v), y = y(u,v), z = z(u,v),
	2) заменить элемент площади dσ на выражение d σ =					ru′× rv′		du dv ;
	2) заменить элемент площади dσ на выражение d σ =					ru′× rv′		du dv ;
	3) вычислить получившийся двойной интеграл по области (S) изменения
	переменных (u,v).

Случай 2. Пусть гладкая поверхность (σ ) задана уравнением, разрешенным от(

носительно z :

z = z(x, y). Присоединив два очевидных тождества, получим па(

раметрические уравнения поверхности (σ )

x = x,

i j k

y = y, (x, y − параметры); тогда

rx′× ry′ =

x′x

y′x z′x

1 0 z′x

= −z′x i

− z′y j

+ k ,

z = z(x, y),

x′y y′y z′y

0 1 z′y

и по формуле (7.34) получим

dσ =

1+ (z′x)2 + (z′y)2 dxdy

. Таким образом,

dσ = 1+ (z′ )2 + (z′ )2

dx dy;

(x, y, z(x, y))

(7.36)

σ∫

f (x, y, z)dσ =

∫∫

1+ (z′ )2

+ (z′ )2

dxdy.

(

)

(σxy)

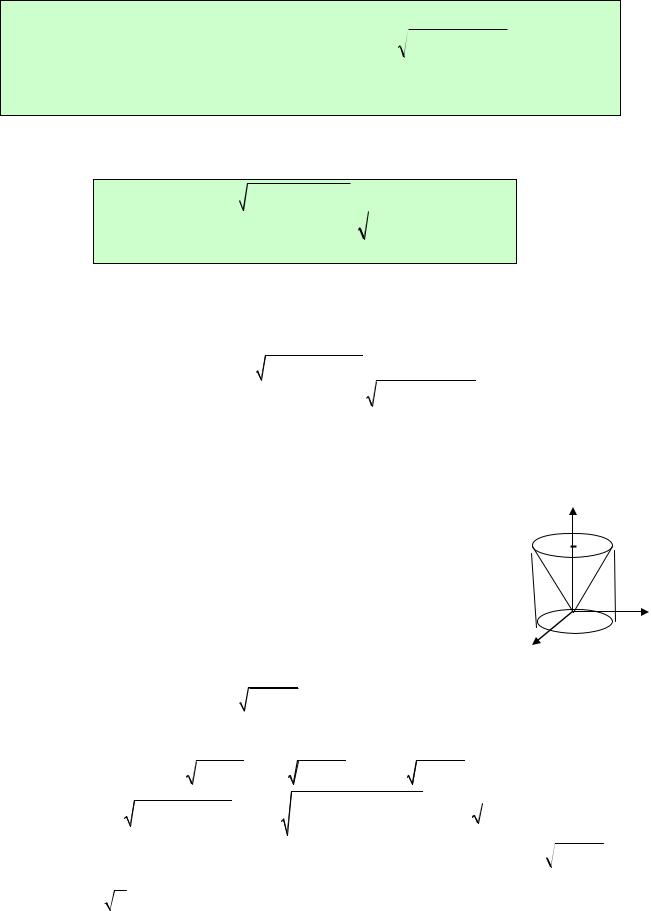
Итак, для вычисления поверхностного интеграла ∫ f (P)dσ = ∫ f (x, y, z)dσ следует:

(σ) (σ)

1)вподынтегральнойфункциизаменить z егозначением z(x, y) наповерхности (σ ),

2)заменить элемент площади dσ на выражение 1+ (z′x)2 + (z′y)2 dxdy,

3)вычислить получившийся двойной интеграл по проекции (σ x y ) поверхности

(σ ) на плоскость XOY .

Случай 3. Пусть гладкая поверхность (σ ) задана уравнением, разрешенным от( носительно x : x = x(y, z). Тогда

dσ = 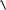1+ (x′y)2 + (x′z)2 dy dz;

∫	f (x, y, z)dσ = ∫∫ f (x(y, z), y, z)	1+ (x′y)	2	+ (x′z)	2	dy dz.	(7.37)
∫	f (x, y, z)dσ = ∫∫ f (x(y, z), y, z)	1+ (x′y)		+ (x′z)		dy dz.
( )	(σ y z)
σ

Здесь (σ yz ) есть проекция поверхности (σ ) на плоскость YOZ .

Случай 4. Пусть гладкая поверхность (σ ) задана уравнением, разрешенным от( носительно y : y = y(x, z) . Тогда

	dσ =	′	2	′	)	2	dxdz;
	dσ =	1+ (y )		+ (y	)		dxdz;
		x		z
∫	f (x, y, z)dσ = ∫∫	f (x, y(x, z), z) 1+ (y′x)2 + (y′z)2 dxdz.						(7.38)
( )	(σx z)
σ

Здесь (σ xz ) есть проекция поверхности (σ ) на плоскость XOZ .

Пример 7.25.Найти массу однородной поверхности x2 + y2 = z2 , (0 ≤ z ≤ 3) , если γ = z .

Решение. Построим поверхность x2 + y2 = z2 методом сечений. В сечении x = 0 получаем y2 = z2 или y = ± z . Это – пара прямых в плоскости YOZ (рис. 52). В сечении z = 3 получаем окружность x2 + y2 = 32 . Таким образом, уравнение x2 + y2 = z2 определяет ко( ническую поверхность. Массу поверхности найдем с помощью поверхностного интеграла: m = ∫ γ dσ = ∫ z dσ .

(σ) (σ)

Для вычисления этого интеграла уравнение поверхности удобно разрешить относительно z : z = x2 + y2 . Найдем z′x , z′y и затем dσ

формул (7.36):

0 y

x	Рис. 52
	Рис. 52

по первой из

z′x =

2x =

z′y =

;

2 x2 + y2

x2 + y2

dσ = 1+ (z′ )2

+ (z′ )2

dxdy =

dxdy = 2 dxdy .

+ y2

x2 + y2

Теперь вычислим ∫ z dσ , подставляя значение z на поверхности (z = x2 + y2 ) и

(σ)

значение dσ = 2 dx dy :

f (x, y,z)

m = ∫	z dσ = ∫∫ x2 + y2	2	dxdy .
(σ)	(σxy)

Здесь (σ xy ) есть проекция конической поверхности (σ ) на плоскость XOY , т.е. круг

радиусом 3

(рис. 52). Двойной интеграл по кругу удобнее вычислять в полярной

системе координат. Для этого заменим x2 + y2

на ρ2 , а dxdy на ρ dρ dϕ . Получим

2π

ρ3

m = 2 ∫∫

+ y

dxdy =

2 ∫∫ ρ dρdϕ = 2

∫ dϕ ∫ρ

dρ =

2 ∫

dϕ =18π 2 .

(σxy)

Пример 7.26. Найти момент инерции относительно начала координат полусфе( ры x2 + y2 + z2 = R2 , (z ≥ 0) , если плотность γ = z .

Решение. Момент инерции относительно начала координат поверхности найдем с помощью поверхностного интеграла по второй из формул (6.13) :

I0 = (σ∫) (x2 + y2 + z2) γ dσ .

На поверхности сферы x2 + y2 + z2 = R2 , γ = z = R2 − x2 − y2 . Поэтому

I0 = (σ∫) R2 R2 − x2 − y2 dσ .

Для вычисления этого интеграла разрешим уравнение поверхности относитель(

но z , найдем z′x , z′y

и затем dσ по первой из формул (7.36):

z′x =

− x

z′y =

−y

z = R2 − x2 − y2 ,

;

R2 − x2 − y2

R dxdy

dσ =

1+ (z′ )2 + (z′ )2 dxdy =

dxdy =

− x2 − y2

R2 − x2 − y2

Подставляя выражение для dσ в интеграл, получим

Rdxdy

== R3

I =

R2 − x2 − y2 dσ = R2

R2 − x2 − y2

dxdy .

(σ∫)

(σ∫∫x y)

R2 − x2 − y2

(σ∫∫x y)

Проекция (σ x y )

(σ∫∫xy)

полусферы на плоскость XOY

есть круг радиусом R ;

dxdy

равен площади π R2

(σ∫∫x y)

π R2

= π R5 .

этого круга. Поэтому

I0 = R3

dxdy = R3

Глава 3. ТЕОРИЯ СКАЛЯРНОГО И ВЕКТОРНОГО ПОЛЯ

8. Скалярное поле

Скалярное поле – это область пространства, в которой задана скалярная функция f (x, y,z) , называемая функцией поля. Например, это может быть поле температур, поле давлений и т.д.

Множество точек поля, в которых функция поля принимает посто( янное значение c , образует поверхность с уравнением f (x, y,z) = c , называемую поверхностью уровня поля. Если плоское скалярное поле, например, находится

в плоскости XOY , то его функция поля f (x, y) зависит от двух переменных x и y , а множество точек, в которых f (x, y) = c , образуют линию уровня. Линии уровня используются при составлении географических карт (для изображения точек, расположенных на одинаковой высоте над уровнем моря), при составлении ме( теорологических карт (для изображения линий одинаковых температур – изо( терм и линий одинакового давления – изобар).

8.1. Производная поля по направлению

Для характеристики скорости изменения поля f (x, y,z) в направлении век(


тора l введем понятие производной поля по направле(
нию. Пусть задана точка M и вектор	l , выходящий из		l
точки M (рис. 53). Рассмотрим точку	M1, лежащую на		M1
точки M (рис. 53). Рассмотрим точку	M1, лежащую на
векторе l , и величину f (M1) − f (M) = f (M) – приращение		M	l

Рис. 53

функции поля f (M) в точке M в направлении l .

Определение. Производной поля f (M) в точке M в направлении l называют величину

∂ f (M) = lim

f (M)

lim

f (M1) − f

(M)

∂ l

l→0

M 1→M

M1 M

Свойства производной по направлению

1). Скорость изменения функции f (M)

в точке M в направлении l

равна

∂ f

(M) .

∂ l

2).Поле f (M) вточке M внаправлении l

возрастаеттогдаитолькотогда,когда

∂ f

(M) ≥ 0 .

∂ l

3).Поле f (M) вточке M внаправлении l

убывает тогдаитолькотогда,когда

∂ f

(M) ≤ 0 .

∂ l

4).Если l || ox , то ∂∂ lf = ∂∂ xf

; если l

|| oy , то ∂∂ lf = ∂∂ yf .

Действительно, 1) f (M)

есть изменение функции f (M)

на участке MM1 ,

f (M)

есть средняя скорость изменения функции

f (M)

на участке MM1 ,

lim

f (M)

есть скорость изменения функции

f (M) в точке M внаправлении l ;

l→0

2) в направлении l поле

f (M) возрастает

f (M1) > f (M )

(M1)− f (M )

> 0

∂ f

(M) ≥ 0

;

M M1

∂ l

3) следующее свойство проверяется так же, как предыдущее свойство;

4) если, например, l || ox , то

f =

f и потому

∂ f

= ∂ f .

∂ l

∂ x

Формула для вычисления производной по направлению

Пусть функция f (M) = f (x, y,z)

– дифференцируема в точке M(x, y,z) . Тогда

f (M) = f ′

(M) x + f′

(M) y + f

′ (M) z + o(ρ) ,

(8.1)

где ρ = ( x)2 + ( y)2 + ( z)2 = l

Поделим равенство (8.1) на l

и lim	o(ρ) = lim	o( l)	= 0.

ρ→0	ρ l→0	l

f (M)

= fx′ (M)

x + fy′ (M)

+ fz′ (M) z

o( l)

(8.2)

Рассмотрим вектор grad f (M) ={fx′ (M), fy′ (M),

fz′ (M)},

называемый

градиентом

, равный единичному вектору направления l .

поля f (M) , и вектор l

{ l

l }

Тогда равенство (8.2) можно записать в виде

f (M)

o( l)

= grad f (M) l

где первое слагаемое есть скалярное произведение векторов grad f (M)

и l0 .

В пределе при l , стремящемся к нулю, получим:

∂ f (M)

= grad f (M) l

(8.3)

∂ l

где grad f (M) ={fx′ (M),

fy′ (M),

fz′ (M)}─ градиент скалярного поля f (M ), l0 =

─ единичный вектор направления l .

8.2. Градиент скалярного поля и его свойства

Вектор grad f (M) ={fx′ (M),

fy′ (M), fz′ (M)} является важной характеристикой ска(

∂

лярного поля. Введем условный оператор =

k (оператор Гамильто(

∂y

∂z

∂x

на или вектор “набла”). С его помощью удобно записать градиент скалярного поля

∂

grad f = {

f ,

∂

f }= f.

∂x

∂y

∂z

Отметим ряд свойств градиента.

1). Скалярное поле f (M) в точке M0

быстрее всего возрастает в направ(

лении вектора grad f (M0) со скоростью, равной

grad f (M0)

2). Скалярное поле f (M) в точке M0 быстрее всего убывает в направлении,

противоположном вектору grad f (M0) , со скоростью, равной

grad f (M0)

3). Вектор grad f (M0)			направлен по нормали к поверхности уровня поля
f (M) , проходящей через точку M0 .
4). Дифференциальные свойства:
4.1) grad(u + v) = gradu + grad v,						4.2) grad(u v) = u gradv + v gradu,
4.3) grad(u)=		v gradu − u gradv			,	4.4) grad f (u) = fu′ gradu,
			v	2
v
4.5) grad r =	r	,				4.6) grad(a r) = a.
	r

Проверим эти свойства.

1. Из формулы (8.3) и определения скалярного произведения следует, что

∂ f (M0)

= grad f (M ) l

grad f (M )

cosϕ ,

∂l

где ϕ ─ угол между векторами grad f (M0)

и l . Так как длина единичного векто(

ра l0 равна единице, то

∂ f (M0)

grad f (M )

cosϕ .

∂ l

Поэтому

∂ f (M0)

принимает наибольшее значение, равное

grad f (M )

, когда cosϕ =1,

∂l

то есть угол ϕ между векторами grad f (M0)

и l равен нулю и grad f (M0) ↑↑ l .

2. Производная	∂ f (M0)	будет принимать наименьшее значение, когда cosϕ = −1,

	∂l
т.е. угол ϕ =π и grad f (M0) ↑↓ l .
3. Поверхность уровня поля			f (x, y,z)		имеет уравнение f (x, y,z) = c . Нормальный
			= { f′	, f ′ ,	f ′}
вектор этой поверхности N							совпадает с grad f (M ) . Значит, вектор
			x	y	z	M0	0

grad f (M0) направлен по нормали к поверхности уровня поля f (M) , проведенной в точке M0 .

4.1. grad(u + v) = {(u + v)′x , (u + v)′y , (u + v)′z }= {u′x , u′y , u′z}+{v′x , v′y , v′z} = gradu + gradv;

аналогично проверяются свойства 4.2), 4.3), 4.4);

для проверки свойства 4.5)

учтем, что r = {x, y, z},

r′

; аналогично,

r =

x2 + y2 + z2 ,

x2 + y2 + z2

ry′ =

rz′ =

и поэтому grad r = {rx′ ,ry′ ,rz′}

= {

{x, y, z} =

;

4.6. grad(a r )

= grad(a x + a

y + a

z) = {a , a

, a } = a .

Из первого и третьего свойств следует инвариантное определение градиента, т.е. определение, не зависящее от системы координат:

Градиент скалярного поля f (M ) в точке M0 есть вектор, который

а) по величине равен наибольшей скорости возрастания поля f (M ) в точке M0 ,

б) направлен по нормали к поверхности уровня поля f (M) , проходящей че( рез точку M0 , в сторону наибольшего возрастания поля.

Пример 8.1. Найти наибольшую скорость возрастания поля f (r) = r3 в точке A(1,2,2).

Решение. Найдем градиент поля:

grad f (r) = gradr3 = 3r2 grad r = 3r2 rr = 3r r . Наибольшая скорость возрастания поля в точке A равна

grad f (r) A = 3r r A = 3r2 A = 3 (x2 + y2 + z2) A = 27.

Пример 8.2. Доказать оптическое свойство эллипса: лучи, выходящие из одного фокуса эллипса, после отражения от эллипса проходят через другой фокус эллипса.

Решение. Пусть F1, F2 − фокусы эллипса; r1 = F1P, r2 = F2P (рис. 54). Рассмотрим

скалярное поле f (P) = r1 + r2 . По определению эллипса точка P принадлежит эллипсу тогда и только тогда, когда f (P) = r1 + r2 = const , т.е. эллипс есть линия

уровня скалярного поля f (P) ; поэтому grad(r1 + r2)=	r1	+	r2	направлен по норма(
	r		r
1		2

ли к эллипсу в точке P . Кроме того, этот вектор направлен по диагонали параллелограмма, построен(

ного на векторах r1 , r2 . Длины этих векторов равны

r1 r2

единице, поэтому параллелограмм является ромбом и его диагональ является биссектрисой угла ромба, т.е.α1 = α 2 . Тогда β1 = β 2 , как углы дополнительные

до прямого. Так как γ 1 = β1, γ 2 = β 2 , то γ 1 = γ 2 , т.е. луч, выходящий из фокуса F1 эллипса, после отра( жения от эллипса пройдет через другой фокус F2 .

					grad(r1 + r2)
	r2						r1
	r2	β1	α1	α	2		r1
	r2		α1	α	2		r1
					β	2	r1
		γ 2	•		β	2
			•	γ 1
			P
			P
•		r1	r	2
				2	•
					•
F1					F2

Рис. 54

9. Векторное поле и векторные линии

Векторное поле – это область пространства, в каждой точке M которой за( дан вектор a(M) .

Пример 9.1. Пусть на материальную точку в области D действует сила F(M ).

Тогда в области D определено векторное поле F(M ).

Пример 9.2. Пусть в области D происходит течение жидкости и в каждой точке M задан вектор v(M ) скорости частицы жидкости. Тогда в области D опреде( лено векторное поле скоростей жидкости.

Пример 9.3. Поместим заряд + q в начало координат. Тогда сила, с которой этот заряд действует на единичный положительный заряд, помещенный в точку M , определяется по закону Кулона:

	q	r
E =			,
E =	r2	r	,
	r2	r

где r ─ вектор, идущий из начала координат в точку M (радиус(вектор точки M ), r ─ его длина. Имеем векторное поле напряженностей E(M) , создаваемое зарядом q .

Мы будем рассматривать только стационарные поля, для которых вектор поля a(M ) зависит от точки M и не зависит от времени. Проекции вектора a(M ) на оси координат обозначим P(M ), Q(M ), R(M ). Тогда:

a(M ) = P(M )i +Q(M ) j + R(M )k .

Далее всюду предполагаем, что функции P, Q, R непрерывны вместе со свои( ми частными производными; в противном случае точку поля назовем особой.

Одной из характеристик векторного поля являются векторные линии.

Векторной линией векторного поля называют линию, в каждой точке которой касательный вектор коллинеарен вектору поля (рис. 55).

dxP = dyQ = dzR

Векторные линии в конкретных полях имеют ясный физический смысл.

В поле скоростей текущей жидкости векторные линии –	a (M )
это линии тока этой жидкости, т. е. линии, по которым
движутся частицы жидкости.	M
	M
В электрическом поле векторные линии – это сило(
вые линии и их расположение очень важно в физике.	Рис. 55

	Выведем	уравнения векторных линий	для	поля
a					не выписаны).
	(M) = Pi + Q j + Rk (для краткости аргументы функций P, Q, R
	Пусть уравнения векторной линии x = x(t),		y = y(t), z = z(t) ,		(t − параметр). Ка(
сательным вектором этой линии является вектор				r ′(t) = {x′(t), y′(t), z′(t)} и вектор
r ′(t)dt = {x′(t)dt, y′(t)dt, z′(t)dt}={dx, dy, dz}.

По определению векторной линии ее касательный вектор r ′(t)dt и вектор поля a = {P, Q, R} коллинеарны. Поэтому координаты этих векторов пропорциональны, т. е.

. (9.1)

Мы получили систему дифференциальных уравнений для отыскания векторных линий поля a . Как решается такая система, покажем на примерах 9.4 и 9.5.

Пример 9.4. Магнитное поле H(M) создано электрическим током силы J , текущим по бесконечно длинному прямому проводу l . Найти силовые линии этого поля.

Решение. Если провод l принять за ось Oz некоторой декартовой системы ко( ординат, то, как известно из физики,

+ xj .

H(M ) = 2J −yi

x2 + y2

Запишем уравнения векторных линий для поля H(M) :

или

= dy

, dz = 0 .

−2J

−y

x2 + y2

Из первого уравнения имеем xdx = −ydy, ∫xdx = −∫ ydy,

x2 = −y2 + C . Из второго

уравнения z = h. Таким образом, силовые линии поля H(M) есть окружности

x2 + y2 = C , расположенные в плоскостях z = h, параллельных плоскости XOY .

Пример 9.5. Найти векторные линии поля

+ (z − x)2

= zi

j + xk .

Решение. Учитывая, что P = z,

Q = (z − x)2, R = x , запишем систему (9.1):

dx =

= dz .

(z − x)2

В одном из уравнений этой системы

разделим переменные: xdx = zdz .

Теперь проинтегрируем ∫xdx = ∫zdz и получим

или

− z

= C .

n(M )

•

Рис. 56

Чтобы решить другое уравнение системы, воспользуемся известным свойством

пропорций: если	a	=	c	, то	a =	c	=	λ a + 8 c	. В нашем примере удобно взять
								λ b + 8 d
	b		d		b d

λ = 1, 8 = −1 и записать систему уравнений следующим образом:

dy	= dx = dz = dx − dz			или	dy	=	−d(z − x) .
(z − x)2					(z − x)2
	z	x	z − x				(z − x)

Разделим переменные: dy = −(z − x)d(z − x) . Проинтегрируем ∫dy = −∫(z − x)d(z − x) и

получим y = − (z − x)2	+ C . Таким образом, векторные линии данного поля есть
2	2
2
линии пересечения поверхностей x2 − z2 = C		и y = − (z − x)2	+ C .
	1	2	2
		2

10. Поток векторного поля

Всюду в дальнейшем мы будем рассматривать так называемую ориентиро( ванную поверхность, т. е. поверхность, в каждой точке ко( торой выбрано направление нормали с помощью единичного

вектора n(M) , причем n(M) является непрерывной вектор(

функцией точки M (рис. 56). Изменение направления нормалей на противоположное

будем называть изменением ориентации поверхности. Рассмотрим физическую задачу о потоке жидкости,

приводящую к понятию потока поля.

10.1. Задача о количестве жидкости

Пусть в некоторой части пространства течет жидкость, причем скорость ча( стицы жидкости зависит только от точки, через которую протекает жидкость, и не зависит от времени, т. е. v = v (M) . Требуется вычислить количество (объем) жидкости Π σ , протекающее в единицу времени через ориентированную по(

верхность (σ ) в выбранном направлении (предполагается, что жидкость может свободно протекать через эту поверхность).

Рассмотрим сначала простейший случай. Пусть (σ ) ─ плоская площадка с

нормальным вектором n , а скорость течения жидкости

v во всех точках одна и

та же. Тогда количество жидкости, протекающей через эту площадку в единицу

времени, равно (рис. 57) объему цилиндра с основанием σ и

образующей

. Так как высота этого

цилиндра

равна

пр v

(v,n)

, то его объем равен

σ . Эта ве(

личина и равна количеству жидкости, протекающей через (σ ).

Опустив знак абсолютной величины, мы получим величину

(σ )

(v,n) σ , которую называют потоком жидкости через (σ ). Если

угол между векторами v и n ─ острый, то говорят, что жид(

Рис. 57

кость течет в направлении вектора n ; в этом случае (v,n) > 0

и поток совпадает с количеством жидкости. Если угол между векторами v

и n

n(Mk )

тупой, то говорят, что жидкость течет в направлении, противоположном векто( ру n ; в этом случае (v,n) < 0 и поток отличается от количества жидкости зна(

ком. Если векторы v и n перпендикулярны, то жидкость течет вдоль площадки (σ ) и поток равен нулю.

Перейдем теперь к общему случаю. Для вычисления
потока жидкости через произвольную поверхность (σ )
разобьем эту поверхность на n частей ( σ1), ..., ( σn ) с					Mk
разобьем эту поверхность на n частей ( σ1), ..., ( σn ) с
площадями σ1, ..., σn (рис. 58). На каждой площадке
( σk )	выберем произвольную точку Mk . Будем при(
ближенно считать, что все частицы, протекающие через					Рис. 58
малую		площадку ( σk) , имеют		одинаковые скорости
v ≈ v (M	k	); кроме того, площадку будем считать плоской и перпендикулярной
нормальному вектору n(Mk ) .
Тогда поток жидкости через площадку ( σk ) приближенно равен
		Π σ	≈	(v (Mk ),n(Mk )) σk .
			k
Для потока через всю поверхность получим
		n		n
		Πσ = ∑Π σk ≈ ∑ (v (Mk ),n(Mk )) σk .
		k=1		k=1

Это приближенное равенство будет тем точнее, чем меньше d = max{ σ1, ..., σn} . Точное значение потока определяется как предел этой суммы при d → 0:

		n	(v (Mk ),n(Mk )) σk .
Πσ	= lim	∑	(v (Mk ),n(Mk )) σk .
	d→0	k=1
Полученный предел равен	поверхностному интегралу I рода от скалярной

функции (v(M ),n(M )). Таким образом, поток жидкости через поверхность (σ )

вычисляется по формуле

Πσ = ∫ (v,n)dσ	.	(10.1)
(σ)

Отметим, что 1) если суммарный поток Πσ > 0 , то количество жидкости, протекающей в направ(

лении нормали n , больше количества жидкости, протекающей в направлении − n ; 2) если суммарный поток Πσ < 0, то количество жидкости, протекающей в направ( лении нормали n , меньше количества жидкости, протекающей в направлении − n ; 3) если Πσ = 0 , то количества жидкости, протекающей в том и другом направ( лении, одинаковы.

Интеграл в формуле (10.1) является поверхностным интегралом первого ро( да от скалярной функции (v,n) . Его также называют поверхностным интегра(

лом второго рода от вектор(функции v . Аналогичным образом определяют по( ток и для произвольного векторного поля a .

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.2015945.15 Кб57matan.doc
#
23.02.20151.02 Mб15Matan.pdf
#
23.04.20191.37 Mб8matan_AAAAAA.doc
#
23.02.20151.37 Mб22MatAn_practice.pdf
#
23.02.20151.84 Mб18MatAn_thory.pdf
#
23.02.20151.78 Mб26Matan__teoria.pdf
#
01.07.20251.01 Mб0Matematicheskaya_logika_i_teoria_algoritmov.docx
#
23.02.2015698.48 Кб15Matematika_2_semestr_RTF_1_.pdf
#
22.02.201557.34 Кб18matematika_for_all.doc
#
13.03.2016495.31 Кб30matem_statistika[1].docx
#
22.02.2015169.99 Кб52Materialy_SK_Myshlenie_i_rech.docx