Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matan__teoria

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.78 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 125 6 7 8 9 10 11 12 > Следующая >>>

m Ф = ∫ mdФ ≤ ∫ f (P)dФ ≤ ∫ M dФ =M Ф.

(Ф) (Ф) (Ф)

6.Об оценке модуля интеграла

∫f (P)dФ ≤ ∫ f (P) dФ.

(Ф)

Оценка модуля интеграла следует из свойств модуля: −

f (P)

≤ f (P) ≤

f (P)

Тогда из свойства 5 следует

− ∫

dФ ≤ ∫

f (P)dФ ≤ ∫

≤ ∫

f (P)

dФ и значит,

∫

f (P)dФ

f (P)

dФ.

(Ф)

7. Теорема о среднем

Пусть функция

f (P) непрерывна на фигуре (Ф) . Тогда на (Ф) существует

точка Pɶ такая, что

∫

f (P)dФ = f (Pɶ) Ф

или

f (Pɶ)=

∫ f (P)dФ.

(6.5)

(Ф)

Выведем эту формулу. Так как функция f (P) непрерывна на фигуре (Ф) , то

она достигает на этой фигуре наименьшего m и наибольшего M значений. По( этому m ≤ f (P) ≤ M на (Ф) . Тогда из соотношения (6.4) следует:

m Ф ≤ ∫ f (P)dФ ≤ M Ф .

(Ф)

Разделим это неравенство на положительное число Ф :

	m ≤			1			∫ f (P)dФ ≤ M.	(6.6)
	m ≤		Ф				∫ f (P)dФ ≤ M.	(6.6)
			Ф
						(Ф)
Рассмотрим число 8 , равное		1			∫		f (P)dФ. Из равенства	(6.6) следует, что
Рассмотрим число 8 , равное		Ф			∫		f (P)dФ. Из равенства	(6.6) следует, что
		Ф

(Ф)

m ≤ 8 ≤ M . Так как функция f (P) непрерывна на фигуре (Ф) , то она принимает на этой фигуре все промежуточные значения между m и M . В частности, функция f (P) принимает промежуточное значение 8 в некоторой точке Pɶ фи(

гуры (Ф) , то есть f (Pɶ)= 8	. Отсюда f (Pɶ)=	1	∫ f (P)dФ и	∫ f (P)dФ = f (Pɶ) Ф .
		Ф
				(Ф)
			(Ф)
Замечание. Значение	f (Pɶ) из теоремы о среднем называют средним значе(

нием функции f (P) на фигуре (Ф) и обозначают fср . Оно используется в при( кладных задачах.

6.6. Механические приложения интеграла по фигуре

Вычисление массы фигуры

Пусть известна плотность распределения масс γ (P) . Тогда масса фигуры (Ф) , как было установлено в п. 6.2, вычисляется по формуле

	m = ∫ γ (P)dФ.	(6.7)
	(Ф)

Отыскание центра тяжести фигуры
Пусть центр тяжести фигуры находится в точке C с координатами xc ,		yc , zc .
Как и при вычислении массы, разобьем фигуру (Ф) на n малых ячеек		( Фk )


(k = 1, 2,…n) . В каждой ячейке выберем точку Pk		с координатами xk , yk , zk (рис. 21).
В точке Pk сосредоточим массу k − й ячейки mk			≈ γ (Pk ) Фk . Тем самым мы заме(
ним фигуру (Ф) системой материальных точек Pk			(k = 1, 2,…n) . Для такой системы
		n
(пример 5.3) абсцисса центра тяжести равна	1	∑xk mk , где m – масса всей си(
(пример 5.3) абсцисса центра тяжести равна	m	∑xk mk , где m – масса всей си(
	m	k=1
		k=1

стемы. Следовательно, для абсциссы центра тяжести первоначальной фигуры имеем

xc ≈ m1 ∑xk

k=1

mk = m1 ∑xk γ (Pk) Фk .

k=1

Это приближённое равенство будет тем точнее, чем меньше диаметры ячеек; поэтому устремим максимальный из диаметров ячеек к нулю и перейдем к пре( делу. Получим

				xc =	1	∫ x γ (P)dФ.			(6.8)
				xc =	m	∫ x γ (P)dФ.			(6.8)
						(Ф)

Аналогично вычисляются две другие координаты центра тяжести

	yc =	1	∫ y γ (P)dФ,			zc =	1	∫ z γ (P)dФ.	(6.9)
	yc =	m	∫ y γ (P)dФ,			zc =	m	∫ z γ (P)dФ.	(6.9)
			(Ф)					(Ф)

Вычисление моментов инерции фигуры

Выведем, например, формулу для вычисления мо(		z
мента инерции IXOY фигуры относительно плоскости
XOY . Для этого, как и в предыдущем случае, разобьем				iPk
XOY . Для этого, как и в предыдущем случае, разобьем				iPk
фигуру на ячейки, выберем в k − й ячейке точку Pk		z	k
			k
(k = 1, 2,…n) и в ней сосредоточим массу ячейки (рис. 21).		0
Момент инерции этой точки относительно плоскости		0
Момент инерции этой точки относительно плоскости	x	Рис.21
XOY равен квадрату расстояния от точки до плоскости	x	Рис.21
XOY равен квадрату расстояния от точки до плоскости		Рис. 21

XOY , т.е. zk2 , умноженному на массу, сосредоточенную в точке, т.е. на Суммируя моменты инерции выбранных точек, получим

n	n
IXOY ≈ ∑zk2 mk = ∑zk2 γ (Pk) Фk .
k=1	k=1

mk .

В пределе, устремляя диаметры ячеек к нулю, получим точное равенство

IXOY = ∫ z2 γ (P)dФ.	(6.10)
(Ф)

Аналогично вычисляются моменты инерции фигуры, относительно плоскостей

XOY и YOZ , осей OX,OY,OZ и момент инерции I0					относительно начала координат:

		IХОZ = ∫ y2 γ (P)dФ,		IУOZ = ∫	x2 γ (P)dФ;	(6.11)
		(Ф)		(Ф)

	IOX = ∫ (y2		+ z2) γ (P)dФ,	IOУ = ∫ (x2 + z2 ) γ (P)dФ;		(6.12)
		(Ф)		(Ф)

	IOZ = ∫ (x2		+ y2) γ (P)dФ,	I0 = ∫ (x2 + y2 + z2) γ (P)dФ.		(6.13)
		(Ф)		(Ф)

Мы ввели понятие интеграла по фигуре, рассмотрели его свойства и приме( нение. Теперь нужно научиться вычислять интегралы по фигуре. Рассмотрим, как вычисляются определенные, криволинейные, двойные, тройные, поверх( ностные интегралы.

7. Вычисление интегралов по фигуре

7. 1. Определенный интеграл

При введении определенного интеграла мы предполагали, что a < b .

b a a

При a > b полагают ∫ f (x)dx = −∫ f (x)dx . При a = b полагают ∫ f (x)dx = 0.

a b a

Определенный интеграл с переменным верхним пределом

Пусть функция f (t) непрерывна на отрезке [a,b] . Тогда она непрерывна, а значит, и интегрируема на любом отрезке [a, x], где x [a,b] . Рассмотрим ин(

теграл ∫ f (t) dt . Каждому x из отрезка [a,b] соответствует определенное число −

значение этого интеграла, то есть интеграл является функцией от x , определен( ной на [a,b] . Обозначим эту функцию Ф(x) . Итак,

x
∫ f (t)d t = Ф(x).	(7.1)
a

Теорема 7.1. Пусть функция f (t) непрерывна на отрезке [a,b] . Тогда производ(

ная определенного интеграла от этой функции по переменному верхнему пре( делу равна значению подынтегральной функции на верхнем пределе, то есть

	′	x		′
	′		f (t) dt		= f (x)	.	(7.2)
	Ф(x) =	∫	f (t) dt		= f (x)	.	(7.2)
		a		x
Доказательство. Для вычисления производной функции Ф(x)							придадим x

приращение x и вычислим приращение функции Ф(x) , воспользовавшись ра( венством (7.1) и свойством аддитивности интеграла:

[a,b], так как

x+x x

Ф(x) = Ф(x + x) − Ф(x) = ∫ f (t)dt − ∫ f (t)dt =

			a	a
x	x+ x	x		x+x
= ∫ f (t)dt +	∫	f (t) dt − ∫ f (t) dt =		∫ f (t) dt.
	x		a	x
a	x		a	x

Кполученному интегралу применим теорему о среднем:

x+ x

Ф(x) = ∫ f (t)dt = f (		) x , где				заключено между x и
	x			x
x
		Ф (x)			f (			) x	= f (		).
			=				x
										x
		x
						x

Перейдем в этом равенстве к пределу при x → 0, при этом воспользуемся непрерывностью функции f (x) и

тем, что x → x при x → 0 (рис. 22). Тогда

x + x (рис. 22). Тогда

	x
x	x + x	x

РисРис. 22.22


Ф′(x) = lim	Ф (x) =	lim	f (		) = lim f (				) = f (x).
				x				x
x→0	x	x→0					→ x
						x

Формула Ньютона%Лейбница

Теорема 7.2. Пусть функция f (x) непрерывна на отрезке [a,b] и

F (x) − одна из ее первообразных на этом отрезке. Тогда справедлива следующая формула Ньютона(Лейбница

∫ f (x)dx = F(b) − F(a) .

Доказательство. Функция Ф(x) = ∫ f (t)d t является первообразной для функции

f (x) на

F (x) и Ф(x)

Ф′(x) = f (x) в силу равенства (7.2). Две первообразные функции f (x) отличаются на константу, то есть Ф (x) = F (x) + C или

x
∫ f (t) dt = F(x) + C ,	x [a,b].	(7.3)
a
В частности, при x = a равенство (7.3) примет вид:
a
∫ f (t) d t = F(a) + C.		(7.4)
a
		a
Вычтем из равенства (7.3) равенство (7.4) и учтем, что		∫ f (t)dt = 0. Тогда
		a
x
∫ f (t)dt = F(x) − F(a) ,	x [a,b] .
a
При x = b это равенство примет вид
b
∫ f (t)dt = F(b) − F(a) .		(7.5)

Разность F (b)− F (a) принято условно записывать в следующем виде:

F(b) − F(a) = F(t)	b ,	или F(b) − F(a) = [F(t)]	b .
	a		a
		b
Тогда формула (7.5) примет вид		∫ f (t) dt = F(t) \|ba = F(b) − F(a), или, заменяя t
		a

на x , получим формулу Ньютона(Лейбница в виде:

b	b = F(b) − F(a)
b
∫ f (x)dx = F(x)		.	(7.6)
a	a
a

Если вместо произвольной первообразной F (x)		записать неопределенный инте(
грал, то формула Ньютона(Лейбница примет вид
b			b

∫ f (x)dx =				(7.7)
	∫ f (x)dx		a .
a

Формула (7.7) дает простой и удобный метод вычисления определенного инте( грала от непрерывной функции, используя неопределенный интеграл.

Пример 7.1. Вычислить среднее значение функции f (x) =		1	на отрезке [1,e].

	x	1− ln2 x
	x	1− ln2 x

Решение. Среднее значение функции fср вычисляется по формуле (6.5):

												1		b			1				e		dx
										fcp =		1		∫ f (x)dx =			1			∫			dx					.
												b − a					e −1
												b − a					e −1						1− ln			2
														a							1 x		1− ln				x
Для вычисления интеграла воспользуемся формулой Ньютона(Лейбница (7.6) и
тем, что			dx		= d (ln x) . Тогда
			x
e					e																								π
∫		dx			= ∫	d (ln x)			= arcsin(ln x)\|e = arcsin(lne) − arcsin(ln1) = arcsin1− arcsin0 =																					,
∫					= ∫																									,
1 x 1− ln			2	x	1 1− ln		2	x					1																2
1 x 1− ln				x	1 1− ln			x
													fcp =		π			.
													fcp =		(e −	1)		.
													2		(e −	1)
Пример 7.2. Вычислить										3			для функции f											x				0 ≤ x ≤ 1,
Пример 7.2. Вычислить										∫	f (x)dx		для функции f								(x) = e				,			0 ≤ x ≤ 1,
										∫													3 − x, 1 < x ≤ 3.
										0
Решение. Воспользуемся сначала свойством аддитивности интеграла, а затем
формулой (7.6). Тогда
	3			1	3						1		3								−	(3 − x)2				3	= (e −1) − (0 − 2) = e +1 .
	3			1	3						1		3						1			(3 − x)2				3
	∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx = ∫exdx + ∫(3 − x)dx = ex																		0				2			1
	0			0	1						0		1						0				2			1
	0			0	1						0		1

Интегрирование по частям

Пусть u(x), v(x) − дифференцируемые функции. Для неопределенного интеграла была получена формула интегрирования по частям

∫u dv = uv − ∫v du .

Воспользуемся этой формулой и формулой (7.7) Ньютона(Лейбница:

b	b =		b = [uv]	b	b
b					b
∫u dv = ∫u dv		uv − ∫v du			− ∫v du .
a	a		a	a	a
a					a

Мы получили формулу интегрирования по частям для определенного интеграла

b	b
∫u dv = uv\|b	− ∫v du .	(7.8)
a

Рекомендации по применению этой формулы такие же, как для неопреде( ленного интеграла.

Пример 7.3. Вычислить интеграл ∫ x ln x dx .

															′		1			∫x dx =			x2
Решение. Положим	u = ln x,				dv = xdx . Тогда du = (ln x) dx =														dx, v =					.
Решение. Положим	u = ln x,				dv = xdx . Тогда du = (ln x) dx =												x		dx, v =				2	.
																	x						2
Используя формулу (7.7), получим:
2	x2		2		2	x	2	1					1		1	x2		2			3
∫ x ln xdx =		ln x\|		− ∫					dx =		2ln 2 −			ln1 −			\|		= 2ln 2	−		.
∫ x ln xdx =	2	ln x\|		− ∫		2		x	dx =		2ln 2 −		2	ln1 −	2	2	\|		= 2ln 2	−	4	.
1	2		1		1	2		x					2		2	2		1			4
1					1
		Интегрирование заменой переменной
Теорема 7.3. Пусть функция								f (x)		непрерывна на отрезке [a,b], а функция
x = ϕ (t) удовлетворяет условиям:
1) множеством значений функции x = ϕ (t)												при t [α, β ]				является отрезок [a,b],

2)ϕ (α ) = a, ϕ(β ) = b ,

3)функция x = ϕ (t) и ее производная ϕ′(t) непрерывны на отрезке [α, β ].

Тогда имеет место следующая формула замены переменной

b	β
∫ f (x)dx = ∫		′	(7.9)
∫ f (x)dx = ∫		f (ϕ (t)) ϕ (t)dt .	(7.9)

aα

Доказательство. Пусть F (x) является первообразной для функции f (x). Тогда

∫ f (x)dx = F (x)+ C , ∫ f (ϕ (t)) ϕ′(t) dt = F(ϕ (t)) + C .

Последнее равенство следует из правила замены переменной в неопределенном интеграле. Используя формулу Ньютона(Лейбница, получим

b	β
∫ f (x)dx = F(b) − F(a) ,	∫ f (ϕ (t)) ϕ′(t) dt = F (ϕ (β ))− F (ϕ (α )) = F (b)− F (a).
a	α

Из сравнения этих двух соотношений следует равенство (7.9).

Итак, при замене переменной в определенном интеграле следует

1)заменить переменную x на удачно подобранную функцию ϕ (t);

2)заменить dx на dϕ (t) = ϕ′(t)d t ;

3)заменить отрезок [a,b] изменения переменной x на отрезок [α,β] из(

менения переменной t, найдя α и β из условий ϕ (α) = a, ϕ (β) = b ; 4) вычислить получившийся определенный интеграл.

Отметим, что при вычислении определенного интеграла по формуле (7.9) не надо возвращаться к старой переменной, как это приходилось делать при за( мене переменной в неопределенном интеграле. Рекомендации по выбору новой переменной такие же, как и для неопределенного интеграла.

Пример 7.4. Вычислить интеграл ∫

d x .

x −1

Решение. Введем новую переменную t, положив

x = t . Тогда x = t2,

dx = 2t d t .

Найдем пределы изменения новой переменной t =

: при x = 4

имеем t = 2 ;

при x = 9 имеем t = 3 . Поэтому, в соответствии с формулой (7.9)

3 t 2t d t

3 (t

2 −1) +1

(t +1+

)d t = 2

dx =

= 2

d t = 2

+ t + ln(t −1)

= 7 + 2ln 2.

∫

∫ t −1

∫

t −1

∫

t −1

x −1

Пример 7.5. Вычислить интеграл ∫

4 − x2 dx .

Решение. Чтобы исчез корень под знаком интеграла, положим x = 2sin t . Тогда

4 − x2 =

4 − 4sin2 t = 2cost . Найдем dx = 2cost dt и пределы изменения новой пе(

ременной: при x = 0 имеем sin t = 0 , t = 0 ; при x = 1 имеем sint = 1 , t = π / 6 .

sin 2t 6

= π +

Тогда ∫

4 − x

dx = ∫ 2cost 2cost dt =

2 ∫(1+ cos2t)dt = 2 t

С помощью замены переменной выведем ряд полезных следствий.

Следствие 1. Если функция f (x)

− нечетная на отрезке [−a,a], то ∫

f (x)dx = 0 .

−a

Действительно, имеем: I = ∫

f (x)dx = ∫ f (x)dx + ∫ f (x)dx = I1 + I2 .

−a

В интеграле I1 сделаем замену переменной x = −t . Тогда dx = −dt

и, в силу нечетно(

сти функции, f (x) = f (−t) = − f (t). При x = −a

имеем t = a ;

при x = 0

имеем t = 0 .

Поэтому

I1 = ∫

f (x)dx = ∫ f (t)dt = −∫ f (t)dt = −I2 ,

I = I1 + I2 = 0 .

−a

Следствие 2. Если функция f (x)

− четная на [−a,a], то

∫

f (x)dx = 2 ∫ f (x)dx .

−a

Эта формула выводится так же, как предыдущая.

				π / 4	x7 − 3x5 + 2x3 − x + 4
Пример 7.6. Вычислить интеграл I = ∫								dx .
Пример 7.6. Вычислить интеграл I = ∫					cos	2	x	dx .
				−π /4	cos		x
				−π /4
Решение. Функция	x7	− 3x5 + 2x3 − x		является нечетной, так как числитель есть
Решение. Функция		cos2	x	является нечетной, так как числитель есть
		cos2	x

функция нечетная, а знаменатель – функция четная. Поэтому интеграл от этой

функции по промежутку

− π

,π

равен нулю. Функция

является четной,

cos

π / 4

4dx

π / 4

4dx

= 8tg x|π0

/ 4 = 8.

поэтому I = ∫

= 2 ∫

−π / 4 cos x

0 cos x

Следствие 3. Пусть функция f (x) имеет период T. Тогда

a+T

∫

f (x)dx = ∫ f (x)dx для любого числа a .

Для вывода этой формулы воспользуемся свойством аддитивности интеграла

	a+T	0	T	a+T
	∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx + ∫ f (x)dx = I1 + I2 + I3 .
	a	a	0	T
В интеграле I3 сделаем замену			x = y + T . Тогда dx = dy , а в силу периодичности
функции	f (x) = f (y + T ) = f (y) . При x = T			имеем y = 0 ; при x = a + T имеем y = a .
	a+T	a	a	0
Поэтому	I3 = ∫ f (x)dx = ∫ f (y)dy = ∫ f (x)dx = −∫ f (x)dx = −I1 I1 + I3 = 0,
	T	0	0	a
		a+T		T
		∫ f (x)dx = I1 + I2 + I3 = I2 = ∫ f (x)dx.
		a		0
		2π
Пример 7.7. Вычислить		∫ sin5 xdx .
		0
Решение. Функция sin5 x		имеет период 2π , равный длине промежутка интегри(

рования. Используя следствие 3, сдвинем промежуток интегрирования вдоль оси

OX на −π		и, так как функция sin5 x − нечетная, воспользуемся следствием 1.
	2π		π
Поэтому	∫	sin5 xdx=	∫
Поэтому		sin5 xdx=		sin5 x dx= 0 .
	0		−π нечетная

Геометрические приложения определенного интеграла Площадь плоской фигуры

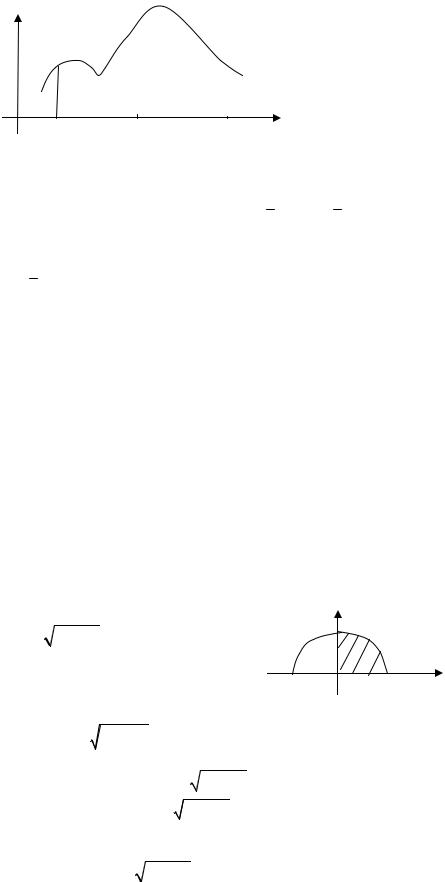
Пусть фигура в плоскости XOY ограничена линиями y = y(x), y = 0, x = a, x = b , причем y(x) − непрерывная неотрицательная функция на [a,b] (рис. 23). Разобьем отрезок [a,b] на n частичных отрезков с длинами x1 , x2 ,..., xn . Через точки деления проведем вертикальные прямые, которые разделят фигуру на n

y= y(x)

xn x

Рис. 23

вертикальных полосок. Каждую k (ю вертикальную полоску заменим прямо( угольником с основанием, равным xk , и высотой, равной y(xk) , где xk − про( извольно выбранная точка на k (м частичном отрезке. Площадь такого прямо( угольника

Sk = y (xk) xk (k = 1,2,...,n).

			n	n
Суммируя площади всех прямоугольников, получим ∑ Sk = ∑ y (						k) xk.
Суммируя площади всех прямоугольников, получим ∑ Sk = ∑ y (					x	k) xk.
			k=1	k=1
Площадь S		заданной фигуры определяется как	предел	полученной суммы
n
S = lim ∑ y(		k) xk при стремлении к нулю d = max	{ xk} . Мы получили предел
S = lim ∑ y(	x	k) xk при стремлении к нулю d = max	{ xk} . Мы получили предел
d→0 k=1		1≤k≤n

интегральной суммы непрерывной функции y (x) по отрезку [a,b], то есть инте(

грал ∫ y (x) dx . Таким образом, площадь фигуры, ограниченной линиями

y = y (x), y = 0, x = a, x = b , при условии, что y (x) ≥ 0 , вычисляется по формуле

S = ∫ y (x)dx

или S = ∫ ydx .

(7.10)

Пример 7.8. Вычислить интеграл ∫ a2 − x2dx.

Решение. Интеграл такого типа был вычислен заменой пере(

−a

менной x = a sin t в примере 7.5. Рассмотрим другой способ.

Рис. 24

Исходя из формулы (7.10), интеграл ∫

a2 − x2 dx численно

y = 0, x = 0, x = a .

равен площади фигуры, ограниченной линиями

y = a2 − x2 ,

Построим эти линии, учитывая, что уравнение y = a2 − x2 определяет ту часть

окружности x2 + y2 = a2 , где y ≥ 0 (рис. 24). Полученная фигура есть четверть

круга с площадью S = π a2 . Таким образом, ∫ a2

− x2dx = π a2 .

Перейдем к более общему случаю. Пусть фигура в плоскости XOY

ограни(

чена линиями y = y1(x), y = y2(x), x = a, x = b, причем y2(x) ≥ y1(x)

на [a,b]

(рис. 25).

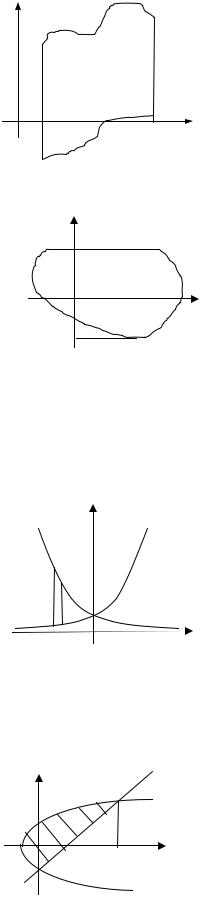
Как и в предыдущем случае, можно получить следующую y

y = y2(x)

формулу для площади S такой фигуры:

(x)− y (x) dx.

S =

∫

(7.11)

Иногда вычисления

значительно упрощаются,

если

поменять ролями оси OX

и OY . Пусть фигура в плоскости

XOY ограничена линиями x = x1 (y),

x = x2 (y),

y = c,

y = d ,

y = y1(x)

причем x2(y) ≥ x1(y) наотрезке [c,d] (рис. 26). Тогда

Рис. 25

S =

(y)− x

(y) dy.

(7.12)

∫

Пример 7.9. Вычислить площадь фигуры, ограниченной ли(

ниями y = ex, y = e−x, x = −1.

x=x1(y)

Решение. Построим заданные линии и заштрихуем фигуру,

x=x2(y)

ограниченную этими линиями (рис. 27). Снизу фигура огра(

ничена линией y = ex = y (x) , сверху – линией

y = e−x = y

(x),

Рис. 26

x [−1, 0]. Для вычисления площади фигуры воспользуемся формулой (7.11):

S = ∫

−1

	2	1		0	(		)		(		)	0
				∫		e−x − ex		dx =		−e−x − ex		= e + e−1 − 2.
y		(x)− y	(x) dx =
				−1								−1

Пример 7.10. Вычислить площадь фигуры, ограниченной линиями

y2 = 2x + 1, y = x −1.						y
Решение. Уравнение y2 = 2x + 1 или y2 = 2(x + 1) определяет па(					y =e−x		y =ex
			2
	−1	,0
раболу с вершиной A	2	,0	, осью симметрии − осью OX (рис.
	2
28). Уравнение y = x −1 определяет прямую, проходящую че(


рез точки (0;−1), (1;0)	. Найдем точки пересечения параболы			−1	0		x
рез точки (0;−1), (1;0)	. Найдем точки пересечения параболы						x

Рис. 27

и прямой, решив систему уравнений: y2 = 2x + 1, y = x −1. По( лучим точку B(0;−1) и точку C (4;3).

Вычислим площадь фигуры по формуле (7.12). Для этого нужно записать урав( нения кривых, ограничивающих фигуру, в виде, разрешенном относительно x . Слева фигура ограничена дугой параболы CAB, на ко(

−1

торой

x =

, справа – отрезком прямой BC, на ко(

тором x = y +1; y меняется от

yB = −1

до

yC = 3 . Поэто(

му по формуле (7.12) имеем

(1/2

2 − 1

(y + 1)2

− 1

= 16 ≈ 5,33.

S =

(y + 1)

−

dy=

− y

Рис. 28

−∫1

−1

<<< < Предыдущая 1 2 3 45 / 125 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.2015945.15 Кб57matan.doc
#
23.02.20151.02 Mб15Matan.pdf
#
23.04.20191.37 Mб8matan_AAAAAA.doc
#
23.02.20151.37 Mб22MatAn_practice.pdf
#
23.02.20151.84 Mб18MatAn_thory.pdf
#
23.02.20151.78 Mб26Matan__teoria.pdf
#
23.02.2015698.48 Кб15Matematika_2_semestr_RTF_1_.pdf
#
22.02.201557.34 Кб18matematika_for_all.doc
#
13.03.2016495.31 Кб30matem_statistika[1].docx
#
01.05.2025232.45 Кб0materialy_dlya_podgotovki_k_testu_po_3_semestru...doc
#
22.02.2015169.99 Кб52Materialy_SK_Myshlenie_i_rech.docx