09_10_Оценки_пар

Проверка выполнения достаточных условий экстремума показывает, что при этих значениях действительно достигается максимум функции правдоподобия.

10.1. Интервальные оценки

При получении точечной оценки необходимо знать лишь выражение для оценки Θ* (X1 ,X 2 ,...,X n ) как функцию данных выборки, а для получения интервальной оценки необходимо также знать закон распределения Θ* (X1 ,X 2 ,...,X n ), с помощью которого рассчитывается вероятность, вид ге-

нерального распределения и значение параметров распределения, которые и подлежат оценке.

Первое затруднение преодолевается тем, что иногда вид генерального распределения может постулироваться (нормальное распределение, равномерное распределение и т.д.). В некоторых случаях при достаточно большом объеме выборки реальную функцию распределения оценки с достаточной точностью можно заменить асимптотической (соответствующей n → ∞). В частности, из теоремы Ляпунова следует, что распределения выборочной

ка wi = nni распределены асимптотически нормально независимо от вида ге-

нерального распределения.

Попытки разрешения второго затруднения приводят к двум способам построения интервальной оценки: приближенному и точному.

Приближенный способ состоит в замене неизвестных параметров гене-

ральной совокупности, от которых зависит распределение Θ* , на их точечные оценки, полученные в результате выборки. Далее оценка строится, как если бы параметры распределения были бы известны.

Точный способ может быть использован лишь в том случае, когда известен закон генерального распределения. При этом строятся вспомогательные случайные величины, распределение которых не зависит от неизвестных параметров генеральной совокупности, но зависит лишь от объема выборки. В частности, при оценке среднего значения нормально распределенной генеральной совокупности можно использовать оценку

которая подчиняется распределению Стьюдента, зависящему только от объема выборки n .

Синтервальной оценкой связано решение трех типов задач:

1)определение доверительной вероятности по заданному доверительному интервалу и объему выборки;

2)определение доверительного интервала по заданной доверительной вероятности и объему выборки;

3)определение необходимого объема выборки по заданным доверительной вероятности и доверительному интервалу.

10.2.Интервальная оценка математического ожидания нормально распределенной случайной величины

при известном σ.

Пусть случайная величина Х генеральной совокупности распределена по

при этом среднее квадратическое отклонение σ считаем известным.

Пусть сделана выборка объема n и вычислена X B , которая является точечной оценкой математического ожидания a генеральной совокупности.

X1 ,X2 ,...,Xn , распределенных так же, как и признак генеральной совокупно-

1). Определим, с какой надежностью математическое ожидание а покры-

где Ф(t) – функция Лапласа. Зная σ, ε и n, можно найти по таблице значений функции Лапласа надежность γ оценки X B математического ожидания a.

2). По выборочному значению математического ожидания X B и извест-

ному σ найти доверительный интервал, который с заданной надежностью γ покрывает математическое ожидание а генеральной совокупности. Это и есть

σ2 = 0,09.

Решение:

1) Определить с вероятностью P = 0,95 доверительные границы для средней

массы деталей X во всей партии. На основании теоремы Ляпунова можно исходить из предположения о нормальном распределении массы деталей.

0,95 средняя масса содержится в промежутке [9,917; 10,083].

2) Определить при тех же условиях, с какой доверительной вероятностью можно гарантировать ошибку выборки, не превышающую 0,05. По величине

ции Лапласа P = 2Ф(1,1785)≈ 0,76 .

3) Определить объем выборки, при котором указанная предельная ошибка ε = 0,05 гарантируется с вероятностью P = 0,95. Из P = 0,95 находим t =

10.3. Интервальная оценка математического ожидания нормально распределенной случайной величины при неизвестном σ.

Для решения поставленной в заголовке задачи используется закон рас-

нения.

Стьюдент (псевдоним английского математика Госсета) показал, что закон распределения случайной величины T (плотность вероятности) описыва-

∞

Здесь Г( x ) = ∫tx −1e−tdt - гамма–функция Эйлера. Это распределение на-

0

зывается распределением Стьюдента. График fn (t ) похож на график плотности вероятности нормального закона, но fn ( t ) определяется только объемом

писать γ = 2∫ fn ( t )dt . Это равенство по-

0

зволяет найти tγ по заданным n и γ. Во всех книгах по математической статистике имеются таблицы, по которым можно найти tγ , зная n и γ. Учитывая,

Таким образом, определив tγ по таблице Стьюдента, можно найти дове-

рительный интервал, покрывающий c надежностью γ математическое ожидание а генеральной совокупности.

Итак, по имеющейся выборке x1 ,x2 ,...,xn находим Хв и sв . Затем, зада-

ваясь надежностью γ, определяем доверительный интервал, покрывающий математическое ожидание а. Другими словами, находим интервальную оценку математического ожидания.

Пример:

Случайная величина Х имеет нормальное распределение. С надежностью γ = 0,95 найти доверительный интервал для оценки неизвестного математиче-

ского ожидания a, если при объеме выборки n=36 получено Хв =24, s = 3. Решение. По таблицам распределения Стьюдента при n = 36 и γ = 0,95 нахо-

дим tγ = 2,03. Тогда точность оценки tγns = 2,0336 3 =1,015 .

Доверительный интервал для a (Хв −1,015; Хв +1,015)= (22,985;25,015).

!Так как при n→∞ распределение Стьюдента стремится к нормальному, то практически при n > 30 можно пользоваться вместо распределения Стьюдента нормальным распределением.

10.4.Интервальная оценка среднего квадратического отклонения σ нормального распределения

Пусть случайная величина Х распределена нормально и требуется оценить неизвестное генеральное среднее квадратическое отклонение (с.к.о.) σ по исправленному выборочному с.к.о. s . Как было показано при рассмотрении точечных оценок, выборочное с.к.о. служит точечной оценкой параметра σ . Поставим теперь вопрос об интервальной оценке σ , т.е., о построении доверительного интервала, покрывающего параметр σ с заданной надежностью γ .

При рассмотрении распределений, связанных с нормальным, обсуждалось распределение χ2 (Пирсона). Рассматривая выборку как совокупность случайных величин X1 ,X 2 ,...,X n , распределенных так же, как и признак гене-

ральной совокупности X, заметим, что величины Xi − X B являются центри-

ма квадратов этих величин пропорциональна исправленной выборочной дис-

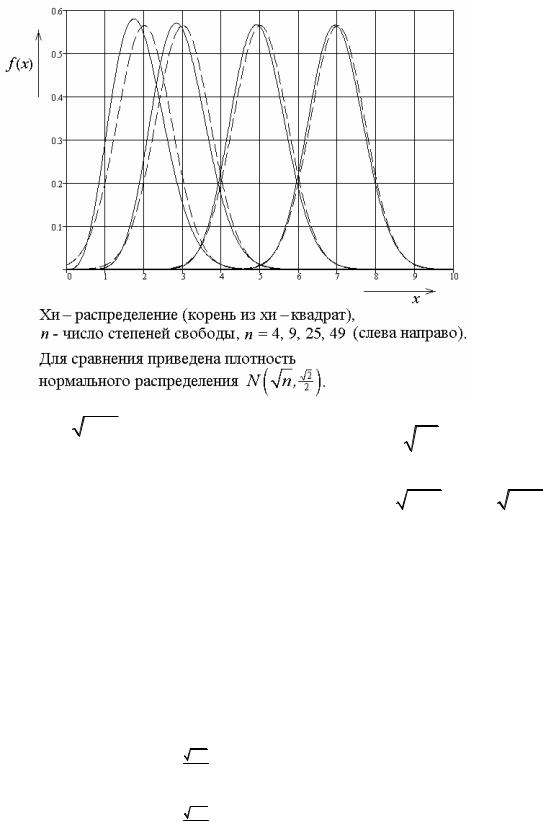
распределения и примерный вид графиков приведены в соответствующем параграфе (распределения, связанные с нормальным).

не зависит от оцениваемого параметра σ , но зависит от объема выборки n . Ниже приведены графики плотности этой величины для нескольких значений объема выборки n .

Исходное условие для доверительного интервала принимает вид:

n−1

1−q

∫ f (x,n)dx =γ .

n−1

1+q

Решения этого уравнения q = q (n,γ ), также как и квантили нормально-

го и связанных с ним распределений можно найти в статистических таблицах и найти ширину симметричного доверительного интервала.

Так как более доступны таблицы квантилей распределения χ2 , изложим еще один способ построения доверительного интервала, покрывающего генеральное с.к.о. σ с заданной доверительной вероятностью. Запишем его в виде:

ния χ2 уровня α и уровня 1−α , соответственно.

! Часто в таблицах приводятся не квантили qp ( P (X < qp )= p ) , а кри-

тические точки распределений kp ( P (X > kp )= p ). Неравенства пре-

дыдущего раздела с использованием критических точек будут выглядеть так:

P (χ2кр(−) < χ2 < χ2кр(+) )=γ ,

P (χ2 > χ2кр(+) )= 1−2γ =α ,

P (χ2 > χ2кр(−) )=1 −α .

Пример:

s (1−q)<σ < s (1+q), 0,8(1−0,32q)<σ < 0,8(1+0,32) или 0,544 <σ <1,056 . 2). Способ. По γ = 0,95 находим α = 0,025 и критические точки для n = 25 :

Заметим, что оба полученных доверительных интервала с вероятностью 0,95 покрывают неизвестное генеральное с.к.о. σ ; второй интервал, несиммет-

ричный относительно s , несколько уже: 1,056 - 0,544 = 0,512; 1,113 - 0,625 = 0,488.