
09_10_Оценки_пар
.pdf
Лекции 9 – 10 СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
В лекциях рассматриваются одна из основных задач математической статистики – оценка неизвестных параметров выбранной параметрической модели. Обсуждаются виды оценок (точечные и интервальные), необходимые характеристики оценок, методы их получения, решаются типичные задачи.
9.1.Статистические оценки параметров распределения
9.2.Точечные и интервальные оценки. Доверительный интервал, точность оценки, доверительная вероятность (надежность)
9.3.Несмещенные, эффективные и состоятельные оценки
9.4.Точечная оценка генерального среднего по выборочному среднему
9.5.Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии
9.6.Метод моментов для точечной оценки параметров распределения
9.7.Метод максимального правдоподобия для точечной оценки параметров распределения
10.1.Интервальные оценки
10.2.Интервальная оценка математического ожидания нормально распреде-
ленной случайной величины при известном σ.
10.3.Интервальная оценка математического ожидания нормально распределенной случайной величины при неизвестном σ.
10.4.Интервальная оценка среднего квадратического отклонения σ нормального распределения
9.1.Статистические оценки параметров распределения
Пусть имеется генеральная совокупность объема N, исследуется случайная величина X, сделана выборка объема n и получены значения случайной величины x1 , x2 ,…, xn . В предыдущих разделах мы рассматривали эти значе-
ния и относительные частоты их появления как закон распределения новой случайной величины, XВ. В дальнейшем нам понадобится иной взгляд на ситуацию.
ОВыборка – последовательность одинаково распределенных независимых случайных величин X1 ,X 2 ,...,X n , распределение которых совпадает с распределением случайной величины X в генеральной совокупности.

94 Лекции 9 -10
Конкретный набор чисел x1 ,x2 ,...,xn , полученный при выборе n объектов из
генеральной совокупности, именуется реализацией выборки.
При повторном отборе объектов возникнет иная реализация выборки, иной набор чисел x1′,x2′,...,xn′ . Таким образом, введенные ранее числовые ха-
рактеристики выборочного распределения оказываются зависящими от конкретной реализации выборки, т.е., случайными величинами.
При изучении случайной величины X, распределенной в генеральной совокупности, часто из теоретических соображений удается установить вид распределения и по данным выборки необходимо оценить (приближенно найти) его численные параметры. Например, если случайная величина имеет нормальное распределение, то для полного его определения необходимо оценить его математическое ожидание и среднее квадратическое отклонение.
О |
Статистическая |
оценка неизвестного параметра теоретического |
|
распределения – |
функция от наблюдаемых случайных величин |
|
||
|
X1 ,X 2 ,...,X n , т.е., также случайная величина Θ* (X1 , X 2 ,..., X n ), которая |
|
на различных реализациях выборки x1 ,x2 ,...,xn ; x1′,x2′,...,xn′ ;…, принимает значения Θ*1 , Θ*2 ,…; ее значение служит оценкой неизвестного параметра теоретического распределения Θ.
9.2.Точечные и интервальные оценки. Доверительный интервал, точность оценки, доверительная вероятность (надежность)
Существуют 2 вида оценок параметров распределения (числовых характеристик) изучаемого признака генеральной совокупности по данным выборки – точечные и интервальные.
ОТочечная оценка неизвестного параметра Θ – случайная функция
Θ* (X1 , X 2 ,..., X n ), значение которой для любой реализации выборки
принимают за приближенное значение параметра Θ,
Θ ≈ Θ* (x1 ,x2 ,...,xn ).
О Интервальная оценка неизвестного параметра Θ – случайная функ-
ция Θ* (X1 ,X 2 ,...,X n ) такая, что
P (−ε1 < Θ−Θ* (X1 ,X 2 ,...,X n )< ε2 )= γ =1 −α ,
или, иначе
P (Θ* (X1 ,X 2 ,...,X n )−ε1 < Θ< Θ* (X1 ,X 2 ,...,X n )+ε2 )=1 −α ,
т.е., интервал
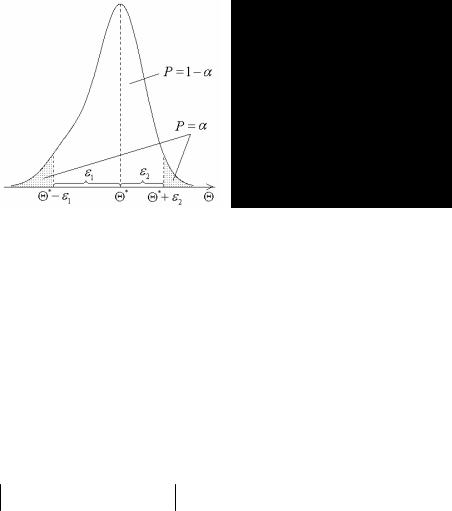
Статистические оценки параметров распределения |
95 |
|||
(Θ* (X1 , X 2 ,..., X n )−ε1 ,Θ* (X1 , X 2 ,..., X n )+ε2 ) |
|
|||
заключает |
в |
себе |
(покрывает) |
|
неизвестный параметр Θ с вероятностью γ . Сам интервал носит название
доверительного интервала, величина γ =1 −α называется доверительной вероятностью оценки (надежностью, коэффициентом доверия), числа
Θ* (X1 ,X 2 ,...,X n )−ε1
иΘ* (X1 ,X 2 ,...,X n )+ε2
– доверительными границами, α – уровнем значимости (существенности).
Смысл этих терминов следующий: Доверительная вероятность характеризует степень доверия к событию (вероятность события), что неизвестный (но не случайный!) параметр Θ содержится внутри доверительного интервала; уровень значимости α характеризует риск наступления события, что параметр Θ в интервале не содержится. Чем более существенны последствия ошибки, что параметр Θ не содержится в доверительном интервале, тем меньшим уровнем значимости нужно задаваться.
З. Если плотность распределения Θ* (X1 ,X 2 ,...,X n ) симметрична относитель-
но своей медианы, применяют следующий способ получения интервальной оценки:
P (Θ* (X1 , X 2 ,..., X n )− Θ <ε)=γ =1 −α ,
P (Θ* (X1 , X 2 ,..., X n )−ε < Θ< Θ* (X1 , X 2 ,..., X n )+ ε)=γ =1 −α ,
т.е. нижняя и верхняя границы доверительного интервала симметричны относительно оценочной функции Θ* (X1 ,X 2 ,...,X n ). Величина ε , характеризующая ширину доверительного интервала, называется точностью оценки. При несимметричной плотности распределения Θ* (X1 ,X 2 ,...,X n ) для нахождения доверительных границ обычно пользуются условиями
P (Θ < Θ* (X1 ,X 2 ,...,X n )−ε1 )= α2 , P (Θ> Θ* (X1 ,X 2 ,...,X n )+ε2 )= α2 .
Точечные оценки проще в вычислении, но не позволяют установить степень достоверности оценки, интервальные оценки. Наряду с возможными границами значений параметра, дают вероятность, с которой истинное (неслучайное!) значение параметра лежит между этими (случайными) границами. Естественно, чем больше надежность оценки, тем шире доверительный интервал, и наоборот, так что практические вычисления являются компромиссом между точностью и надежностью оценки. Наиболее часто задают на-
дежность 0,95; 0,99 и 0,999.

96 |
Лекции 9 -10 |
9.3. Несмещенные, состоятельные и эффективные оценки
Для того, чтобы статистической оценке можно было доверять, она должна обладать некоторыми свойствами.
ОСтатистическая оценка Θ* называется несмещенной, если ее математическое ожидание равно Θ, т.е. M Θ* = Θ.
ОСтатистическая оценка Θ* называется состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е.
ε > 0 nlim→∞ P (Θ* −Θ < ε)=1.
!Из неравенства Чебышева следует, что несмещенная оценка, дисперсия которой стремится к нулю при n → ∞, является состоятельной.
ОСтатистическая оценка Θ* называется эффективной, если при данном объеме выборки из всех возможных оценок она имеет наименьшую дисперсию.
!На практике не всегда удается добиться выполнения всех трех требований к оценке. Соображения практической удобности заставляют пользоваться не полностью адекватными оценками, но необходимо представлять, каким свойством мы пренебрегаем. Ниже, при рассмотрении конкретных оценок, эти аспекты будут обсуждаться.
9.4. Точечная оценка генерального среднего по выборочному среднему
Выберем в качестве оценки генерального среднего |
M [X ]= a среднее |
||||
арифметическое случайных величин X1 ,X 2 ,...,X n : |
|
= |
X1 + X 2 + ...+ X n |
; |
|
X B |
|||||
|
|||||
|
|
|
n |
||
для конкретной реализации выборки значения этой величины равны выборочным средним. Найдем математическое ожидание оценки X B :
|
|
|
|
1 n |
1 |
|
n |
|
1 n |
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||||||
= M |
∑Xi = |
|
M ∑Xi |
= |
|
∑M [Xi ]= |
|
n a = a , |
|||||||||||||
M X B |
n |
|
n |
||||||||||||||||||
|
|
|
|
n i=1 |
|
|
i=1 |
|
|
n i=1 |
|
|
|
|
|||||||
следовательно, |
|
– несмещенная оценка M [X ]. |
|
|
|
|
|
||||||||||||||
X B |
|
|
|
|
|
||||||||||||||||
По теореме Чебышева |
ε > 0 |
|
|
|
|
|
1 |
n |
|
|
n |
|
|
|
=1, |
исполь- |
|||||
|
|
|
|
|
|
|
|||||||||||||||
lim P |
|
|
∑Xi − |
1 ∑M [Xi ] |
< ε |
||||||||||||||||
|
|
|
|
|
|
|
n→∞ |
|
|
n i=1 |
|
|
n i=1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
зуя предыдущее |
равенство, |
это |
|
можно |
записать |
в |
виде |
||||||||||||||

Статистические оценки параметров распределения |
97 |
|||||||||
nlim→∞ P ( |
|
|
|
− M [X ] |
|
< ε)=1, т.е., по определению, |
|
– состоятельная оцен- |
||
|
|
|
||||||||
X B |
X B |
|||||||||
ка |
M [X ]. Если случайная величина X распределена нормально, то оценка |
|||||||||
|
|
будет и эффективной. На практике во всех случаях для оценки матема- |
||||||||
|
X B |
|||||||||
тического ожидания используется среднее арифметическое X B (обозначается также X ).
9.5.Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии
|
1 |
n |
||
Покажем, что выборочная дисперсия DB = |
∑(Xi − |
|
)2 (среднее зна- |
|
X B |
||||
|
n i=1 |
|||
чение квадрата отклонения) является смещенной оценкой генеральной дисперсии. Найдем математическое ожидание DB :
|
|
|
|
1 |
n |
|
|
|
|
2 |
|
|
|
n |
|
1 |
n |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
M [DB ]= |
M |
∑(Xi − X B ) |
|
= M |
1 |
∑Xi |
2 − |
∑Xi |
|
= |
||||||||||||
n |
|
n |
||||||||||||||||||||
|
|
|
|
= |
1 |
|
|
|
|
|
|
n |
= |
|
= |
|
|
|
||||
|
|
|
|
i |
|
|
|
|
|
|
i 1 |
|
i 1 |
|
|
|||||||
|
1 |
n |
|
|
|
1 |
|
n |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
M ∑Xi 2 |
− |
M ∑Xi |
= |
M (X12 |
+ X 22 |
+ ... + X n2 )− |
|||||||||||||||
n |
2 |
n |
||||||||||||||||||||
|
i=1 |
|
|
n |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
− |
|
|
|
|
M |
X 2 |
+ X 2 |
+ ... + |
|
X 2 |
+ 2 |
X |
X |
|
+ |
X |
X |
|
+ X |
|
X |
|
+ ... |
+ |
X |
|
X |
|
|
= |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
2 |
2 |
3 |
n−1 |
n |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
(MX12 + MX 22 + ... + MX n2 )− |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
(MX1 MX 2 + MX1 MX 2 + MX 2 MX 3 |
+ ... + MXn−1 MXn )= |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
1 |
|
MX |
2 |
+ MX |
2 |
|
+...+ MX |
− |
2 |
|
|
MX |
MX |
+ MX MX + |
...+ MX |
MX |
|
= |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
(n−1) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n (n −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
n −1 |
|
n MX 2 − |
2 |
|
|
(MX )2 = |
n −1 |
|
MX 2 |
− |
n −1 |
(MX )2 = |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
n2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
n −1 |
|
(MX 2 |
|
− (MX )2 )= |
n −1 |
DX . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как M [DB ]≠ DX , выборочная дисперсия является смещенной оцен-
кой генеральной дисперсии. Для получения несмещенной оценки достаточ-

98 |
|
|
|
|
|
|
|
|
|
Лекции 9 -10 |
но перейти к исправленной выборочной дисперсии, s2 = |
n |
|
D , |
|||||||
|
|
|||||||||
|
n |
|
|
1 |
n |
n −1 B |
||||
s2 = |
DB = |
∑(Xi − |
|
)2 . |
|
|
|
|||
X B |
|
|
|
|||||||
n −1 |
|
|
|
|
||||||
|
|
n −1 i=1 |
|
|
|
|||||
Очевидно, исправленная |
выборочная дисперсия |
является несме- |
||||||||
щенной оценкой генеральной дисперсии.
Покажем, что исправленная выборочная дисперсия является состоятельной оценкой генеральной дисперсии. Рассмотрим выборочную дис-
персию; для ее состоятельности необходимо, чтобы для ε > 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim P( |
|
DB − DX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− X B ) |
− M |
(X − M |
|
|
|
|
|
=1, |
||||||||||||||||||||||||||||||||
|
|
<ε)=1 lim P |
|
∑(Xi |
|
[X ]) |
<ε |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
n→∞ |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
n→∞ |
|
|
n i=1 |
|
(( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
n→∞ |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
B ) |
|
|
|
|
( |
|
[ |
|
|
]) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∑ |
X |
|
− M |
|
|
|
|
|
− |
X |
|
|
− |
M |
X |
|
|
<ε |
|
=1, |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
lim P |
|
|
|
n i=1 |
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
(α |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
* |
[X ]) |
2 |
−(α1 |
[X ]) |
2 |
|
<ε |
|
=1. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
lim P |
|
2 [X ]−α2 [X ])− |
(α1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
||||||
|
|
|
|
( |
|
|
[X ]−α |
|
|
[X ] |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
) |
2 − |
( |
|
|
) |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
n→∞ |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Так как lim P |
|
α* |
|
|
|
<ε |
|
|
=1 и |
|
lim P |
|
|
|
|
α |
* [X ] |
|
|
α |
[X ] |
2 |
|
<ε |
|
=1, то |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
α2 [X ]) |
|
|
( |
|
[X ]) |
2 |
|
−(α1 [X ]) |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
− |
* |
|
2 |
|
|
=1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
и lim P |
(α2 [X ]− |
(α1 |
|
|
|
|
|
<ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
т.е., выборочная дисперсия – состоятельная оценка генеральной диспер-
сии. Так как lim |
n |
|
=1, lim s2 |
= lim |
n |
|
lim D = DX , следовательно, и ис- |
|
|
|
|||||||
n→∞ n −1 |
n→∞ |
n→∞ n −1 |
n→∞ |
B |
||||
правленная выборочная дисперсия является состоятельной оценкой генеральной дисперсии.
!Оценка s2 = n n−1 DB для генеральной совокупности не является эффек-
тивной, но для нормального распределения величины X оценка явля-
ется асимптотически эффективной, т.е., при n → ∞ отношение дис-
персии этой оценки к минимально возможной дисперсии оценки стремится к единице.
9.6.Метод моментов для точечной оценки параметров распределения
Врамках этого метода, предложенного К. Пирсоном, в качестве точечных оценок теоретических моментов рассматриваемого распределения берутся эмпирические, выборочные моменты того же порядка. Можно показать, что начальные и центральные выборочные моменты являются состоятельными оценками соответствующих теоретических моментов.

Статистические оценки параметров распределения |
99 |
Оценка одного параметра. Пусть известен вид плотности распределения f (x,θ), зависящей от одного параметра θ , но не известно значение этого
параметра. Для нахождения оценки этого параметра достаточно составить одно уравнение, например, для начальных моментов первого порядка: xB = M (X ). Так как математическое ожидание признака генеральной сово-
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
купности M (X ) |
= ∫ x f (x,θ)dx =ϕ (θ) зависит от неизвестного параметра |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ , а выборочное среднее xB |
= |
x1 + x2 + ... + xn |
|
|
зависит от реализации выбор- |
|||||||||||||||||||||||||||||
|
|
|
|
|
n |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 + x2 |
+ ... + xn |
|
||||||
ки x ,x |
2 |
,...,x |
n |
, то после решения уравнения ϕ |
(θ)= |
мы полу- |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||
чаем θ* |
=ψ (x ,x |
2 |
,...,x |
n |
), оценку неизвестного параметра как функцию зна- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
чений конкретной выборки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Случайная величина |
|
|
|
|
X распределена по показательному закону с плотно- |
|||||||||||||||||||||||||
|
|
|
|
стью распределения |
|
|
|
f (x)= λe−λx (x ≥ 0) |
|
и неизвестным параметром λ . Ме- |
||||||||||||||||||||||||
|
|
|
|
тодом моментов по выборке x1 ,x2 ,...,xn оценить значение этого параметра. |
||||||||||||||||||||||||||||||
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
M (X )= ∞∫xλe−λx dx = |
|
|
|
λx = t |
|
|
|
= |
1 |
∞∫te−t dt = |
|
1 |
= xB , т.е. λ = |
1 |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
λ 0 |
|
λ |
|
xB |
|||||||||
|
|
|
|
Итак, оценка параметра распределения λ* = |
1 |
. |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xB |
|
|
|
|
|||
Оценка двух параметров. Пусть задан вид плотности распределения, зависящей от двух неизвестных параметров, f (x,θ1 ,θ2 ). Для их оценки можно,
например, приравнять начальные моменты первого порядка и центральные моменты второго порядка, т.е.,
|
|
|
1 |
n |
|
αk* [X ]= xk = |
∑(xi )k , µ2* [X ]= µ2 |
[X ], или M (X )= xB , D (X )= DB . |
|||
|
|
|
n i=1 |
|
|
Аналогично случаю одного параметра, теоретические моменты есть функции параметров θ1 ,θ2 , а выборочные моменты зависят от реализации выборки.
Решая полученную систему относительно неизвестных параметров, получаем их точечные оценки:
θ * =ψ |
1 |
(x ,x |
2 |
,...,x |
n |
), |
θ * =ψ |
2 |
(x ,x |
2 |
,...,x |
n |
). |
1 |
1 |
|
|
2 |
1 |
|
|
Пример:
Случайная величина X распределена по нормальному закону с плотностью

100 |
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 9 -10 |
|
|
|
f (x)= |
|
1 |
e− |
(x−a)2 |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
распределения |
|
|
2σ2 |
и неизвестными параметрами a и σ . |
|||||||||
σ |
2π |
|
||||||||||||
|
|
|
|
|
|
x1 ,x2 ,...,xn |
|
|
|
|
||||
|
Методом моментов по выборке |
оценить значение этих парамет- |
||||||||||||
|
ров. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Приравняем теоретические и эмпирические средние и дисперсии. |
|||||||||||||
|
Как известно, для нормального распределения M (X )= a , D (X )=σ2 . |
|||||||||||||
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 + x2 +...+ xn |
|
|
n |
||||||||
|
a* |
= xB = |
, σ* = |
DB = |
1 ∑(xi − |
|
)2 . |
|||||||
xB |
||||||||||||||
|
||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
n i=1 |
|||
9.7.Метод максимального правдоподобия для точечной оценки параметров распределения
Метод максимального правдоподобия, предложенный Р. Фишером, может быть применен для точечной оценки параметров распределения как дискретных, так и непрерывных случайных величин.
Дискретные случайные величины. Пусть Х – дискретная случайная величина, для которой в результате опыта получена выборка значений x1 ,x2 ,...,xn .
Вид закона распределения известен; закон содержит неизвестный параметр θ , для которого требуется найти точечную оценку на основании данных выборки.
Обозначим вероятность P (X = xi )= p (xi ;θ), i = 1 , 2 , . . . , n .
Функцией правдоподобия дискретной случайной величины Х назы-
вают функцию аргумента θ и данных выборки x1 ,x2 ,...,xn :
L (x1 ,x2 ,...,xn ;θ)= p (x1 ;θ) p (x2 ;θ) ... p (xn ;θ).
В качестве точечной оценки параметра θ принимается значение θ* =θ* (x1 ,x2 ,...,xn ), при котором функция правдоподобия достигает наи-
большего значения. Полученную оценку называют оценкой максимального
правдоподобия.
Так как функции L и ln L достигают максимума при одном и том же значении θ , при практических вычислениях чаще используют вторую функ-
цию, называемую логарифмической функцией правдоподобия: ln L (x1 ,x2 ,...,xn ;θ)= ln p (x1 ;θ)+ln p (x2 ;θ)+ ...+ln p (xn ;θ).
!После решения уравнения ddlnθL = 0 , называемого уравнением правдо-
подобия, которое дает критические точки функции правдоподобия, не-
обходимо отобрать точки максимума, пользуясь условием |
d 2 ln L |
< 0. |
|
dθ2 |
|||
|
|
Полученная точка максимума θ* дает оценку максимального правдопо-

Статистические оценки параметров распределения |
101 |
добия параметра θ .
!Оценки, полученные методом максимального правдоподобия:
1)состоятельны (но могут оказаться смещенными);
2)распределены асимптотически нормально (при n → ∞ закон их распределения приближается к нормальному);
3)среди всех асимптотически нормальных оценок оценки, полученные методом максимального правдоподобия, имеют наименьшую диспер-
сию, т.е., если для параметра θ существует эффективная оценка θ*эфф ,
то она совпадает с полученной методом максимального правдоподобия. Метод особенно полезен при малых объемах выборок; к недостаткам метода можно отнести громоздкие вычисления.
Пример:
Случайная величина X распределена по закону Пуассона:
Pm (X = xi )= λxxi ei!−λ ,
где m – длина серии испытаний, xi – число появлений события в i -й серии
испытаний, n– объем выборки (число проведенных серий испытаний), λ – неизвестный параметр распределения. Методом максимального правдоподобия по выборке x1 ,x2 ,...,xn оценить значение этого параметра.
Решение:
Составим логарифмическую функцию правдоподобия:
ln L (x1 ,x2 |
|
λ |
x1 |
e |
−λ |
|
λ |
x2 |
e |
−λ |
|
λ |
xn |
e |
−λ |
|
|
,...,xn ;λ)= ln |
|
|
|
|
|
... |
|
|
|
= |
|||||||
|
|
|
x1! |
|
|
x2! |
|
|
xn! |
|
|
||||||
|
|
λ∑xi |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
−ln (x ! x ! ... x !). |
|
|
= ln |
|
|
|
e−nλ |
= |
|
|
x |
ln λ −nλ |
||||||||
|
x ! x ! ... x ! |
|
|
|||||||||||||||
|
|
|
|
|
(∑ i |
|
|
|
|
1 2 |
n |
|||||||
|
|
1 2 |
n |
|
|
|
= (∑xi )−n = 0 , |
|
||||||||||
Уравнение правдоподобия: |
|
d ln L |
|
|||||||||||||||
|
|
|
|
|
|
dλ |
|
|
λ |
|
|
|
|
|
|
|
||
его решение (критическая точка): |
λ = |
(∑xi ) |
= |
|
. |
|
||||||||||||
xB |
|
|||||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||
Проверим |
выполнение |
|
достаточных |
условий |
экстремума: |
|||||||||||||
d 2 ln L |
= − (∑xi )< 0 , |
|
λ = |
|
|
|
|
|
|
|
||||||||
т.е., |
x |
B |
|
– точка |
максимума, |
и в качестве |
||||||||||||
dλ2 |
|
λ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оценки максимального правдоподобия параметра λ распределения Пуассона нужно взять выборочное среднее λ* = xB .
Непрерывные случайные величины. Пусть Х – непрерывная случай-
ная величина, для которой в результате опыта получена выборка значений x1 ,x2 ,...,xn . Вид плотности распределения известен; плотность содержит не-
известный параметр θ , f (x)= f (x,θ), для которого требуется найти точечную оценку на основании данных выборки.

|
102 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 9 -10 |
|||
|
Функцией правдоподобия непрерывной случайной величины Х на- |
|||||||||||||||||||||||||||
|
зывают функцию аргумента θ и данных выборки x1 ,x2 ,...,xn : |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
L (x1 ,x2 ,...,xn ;θ)= f (x1 ;θ) |
f (x2 ;θ) ... f (xn ;θ ). |
|
|
|
|
||||||||||||||||||||
|
Дальнейшие вычисления аналогичны случаю дискретной случайной ве- |
|||||||||||||||||||||||||||
|
личины. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример: |
|
Случайная величина |
X распределена по показательному закону с плотно- |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
стью распределения |
f (x)= λe−λx |
(x ≥ 0) и неизвестным параметром λ . Ме- |
|||||||||||||||||||||||
|
|
|
тодом максимального правдоподобия по выборке |
x1 ,x2 ,...,xn оценить значе- |
||||||||||||||||||||||||
|
|
|
ние этого параметра. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Решение. Составим логарифмическую функцию правдоподобия: |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
ln L (x1 ,x2 ,...,xn ;λ)= ln(λe−λx1 |
λe−λx2 |
... λe−λxn |
)= |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
= ln (λne−λ∑xi )= nln λ −λ(∑xi ). |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Уравнение правдоподобия: |
d ln L |
= |
|
n |
|
−(∑xi |
)= 0 , |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dλ |
|
λ |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
его решение (критическая точка): λ |
= |
|
n |
|
= (∑xi ) −1 = |
|
1 |
. |
|
|
|
|
|||||||||||||
|
|
|
|
(∑xi ) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
xB |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Проверим выполнение достаточных условий экстремума: |
d 2 ln L |
= − |
n |
< 0 , |
|||||||||||||||||||||
|
|
|
|
dλ2 |
|
λ2 |
||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
т.е., λ = |
|
|
– точка максимума, и в качестве оценки максимального прав- |
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
xB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
доподобия параметра λ показательного распределения нужно взять величи- |
|||||||||||||||||||||||||
|
|
|
ну, обратную выборочному среднему, λ* |
= |
|
1 |
, |
что совпадает с оценкой, |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
полученной методом моментов. |
|
|
|
|
|
|
|
|
xB |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
!Если плотность распределения зависит от двух неизвестных параметров, f (x)= f (x;θ1 ,θ2 ), то и функция правдоподобия является функцией
двух переменных, θ1 ,θ2 . Для нахождения критических точек нужно решить систему
∂ln L = 0,
∂θ1
∂ln L = 0,∂θ2
Для того, чтобы в критической точке достигался максимум, достаточно, чтобы выполнялись условия AC − B2 > 0 , A < 0 (или C < 0 ), где A,B,C – значения вторых производных в критической точке P (θ1 ,θ2 ):
