11_12_Проверка_стат_гипотез

Лекции 11–12 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

11.1.Статистическая гипотеза. Параметрическая и непараметрическая, нулевая и конкурирующая, простая и сложная гипотезы

11.2.Ошибки первого и второго рода

11.3.Статистический критерий. Критическая область. Область принятия гипотезы. Критические точки

11.4.Уровень значимости и мощность критерия

11.5.Виды критических областей

11.6.Методика проверки гипотез

12.1.Некоторые типичные задачи проверки параметрических гипотез

12.1.1Проверка гипотез о доле признака

12.1.2Проверка гипотез о среднем значении

12.1.3Сравнение дисперсий двух совокупностей

12.1.4Сравнение исправленной выборочной дисперсии

с гипотетической генеральной дисперсией нормальной совокупности

12.2.Непараметрические гипотезы. Критерии согласия Пирсона и Колмогорова 12.2.1 Критерий Пирсона 12.2.2. Критерий Колмогорова

11.1.Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы

Задача проверки гипотезы в известном смысле напоминает задачу оценки параметров генеральной совокупности по данным выборки: высказывается некоторое утверждение и на основании данных выборки выносится суждение о справедливости этого утверждения.

Важно отметить, что вопрос должен подлежать рассмотрению методами теории вероятностей. Приведем пример, заимствованный из книги Я.И. Хургина: герой известной книги О. Бендер узнает о существовании в городе Черноморске подпольного миллионера (А.И. Корейко). Он может принять эту гипотезу (и начать преследовать предполагаемого миллионера), может отвергнуть гипотезу (и заняться чем-либо другим), но не может повторить обстоятельства, в которых он получил это известие: даже если он получит аналогичное сообщение от другого собеседника, уровень его информированности будет уже иным. Событие «Корейко – миллионер», несомненно, является

неопределенным для Остапа Ибрагимовича к моменту начала его эскапады, но не является случайным (в смысле, вкладываемом в это понятие в рамках теории вероятности). Гипотеза, принятая О. Бендером («Корейко – миллионер») не является статистической и не подпадает под действие рассматриваемых далее методов.

Статистические гипотезы утверждают что-либо о статистически устойчи-

вых событиях (события, которые могут протекать многократно при идентичных условиях). Как правило, речь идет о виде функции распределения случайной величины или о параметрах, характеризующих эту функцию распределения.

Примеры статистических гипотез:

1)генеральная совокупность распределена по нормальному закону;

2)дисперсии двух нормальных распределений равны;

3) дисперсия признака, распределенного в генеральной совокупности

0 < D < 2.

Введем некоторые определения.

О Если в гипотезе утверждается что-то о значении какого-то параметра, гипотеза называется параметрической. Если гипотеза предполагает что-то, количественно не измеряемое (например, «признак имеет нормальное

распределение»), гипотеза называется непараметрической.

ООсновной (нулевой) гипотезой H0 называют выдвинутую гипотезу.

ОАльтернативной (конкурирующей) гипотезой H1 называют гипотезу, которая противоречит выдвинутой.

ОГипотеза называется простой, если ответ на нее однозначен («признак распределен нормально», «дисперсия распределения равна 2», «распре-

деления двух совокупностей одинаковы», и т.п.). Если ответ неоднозначен, гипотеза называется сложной («признак не распределен нормально», «дисперсия распределения не равна 2», «дисперсия распределения больше 2», «распределения двух совокупностей не одинаковы», и т.п.). Утверждение «дисперсия распределения больше 2» сводится к бесконечному количеству утверждений: «дисперсия распределения равна 2,1», «дисперсия распределения равна 2,2», и т.д.

11.2. Ошибки первого и второго рода

Выдвинутая гипотеза может быть правильной или не правильной, поэтому ее необходимо проверить по эмпирическим данным, т. е. по выборке. Поскольку содержимое выборки случайно, то и высказывания, сделанные на основании исследования выборки, случайны, т.е., они могут быть и правильны, и неправильны. В итоге проверки гипотезы могут быть приняты неверные решения в двух случаях, т.е. могут быть допущены ошибки двух типов. О Ошибкой первого рода называют ошибку, допускаемую в случае, когда

отвергнута правильная основная гипотеза ( H0 отвергнута, хотя она вер-

на).

ООшибкой второго рода называют ошибку, допускаемую в случае при-

нятия неправильной основной гипотезы ( H0 принята, хотя она невер-

на).

11.3. Статистический критерий. Критическая область. Область принятия гипотезы. Критические точки

Для проверки гипотезы H0 используют специально подобранную случайную величину, точное или приближенное распределение которой известно.

ОСлучайная величина Θ, служащая для проверки гипотезы H0 (основной), называется статистическим критерием, или просто критерием. Наблюдаемым значением Θнабл называют значение критерия, вычисленное по выборке.

ОКритической областью S называется множество значений критерия,

при которых основная гипотеза H0 отклоняется.

ООбластью принятия гипотезы (допустимой областью) S называется множество значений критерия, при которых основная гипотеза H0 не

отклоняется.

ОКритические точки разделяют критическую область и область принятия гипотезы.

Основной принцип проверки статистических гипотез состоит в следующем: если наблюдаемое значение критерия Θнабл попадает в критическую область,

то основную гипотезу H0 отклоняют и принимают альтернативную гипотезу H1 , если Θнабл принадлежит области принятия гипотезы − гипотезу H0 принимают, гипотезу H1 отклоняют.

В общем случае критерий представляет собой многомерную случайную величину (например, проверяется предположение сразу о нескольких параметрах генеральной совокупности), однако в дальнейшем будем рассматривать простейшие одномерные критерии. Критическая и допустимая области в этом случае есть одно-

мерные числовые множества. Вид критической области зависит от вида основной и альтернативной гипотез.

11.4. Уровень значимости и мощность критерия

ОВероятность совершить ошибку первого рода называют уровнем значимости критерия и обозначают через α, α = P (H1 H0 ).

Вероятность ошибки второго рода обычно обозначается β, β = P (H0 H1 ).

ОМощностью критерия называют вероятность попадания критерия в

критическую область при условии, что справедлива альтернатив-

ная гипотеза H1 (т.е., мощность критерия – вероятность недопущения

ошибки второго рода). Очевидно, мощность критерия равна 1 - β.

Обычно для α используются стандартные значения: α = 0,05, α = 0,01 и

т.п.. Как бы ни была мала величина α, попадание Θнабл в критическую область есть только маловероятное, но не абсолютно невозможное событие. Поэтому не исключено, что при верной гипотезе H0 значение Θнабл может

оказаться в критической области. Отклоняя в этом случае гипотезу H0 , мы допускаем ошибку первого рода, вероятность которой и характеризуется величиной α. Чем меньше α, тем менее вероятно допустить ошибку первого рода. Однако с уменьшением α уменьшается критическая область, а следовательно, становится менее возможным попадание в нее выборочного значения Θнабл даже когда гипотеза H0 не верна. При α = 0 гипотеза H0 будет всегда

приниматься независимо от результатов выборки. Поэтому уменьшение α влечет за собой увеличение вероятности ошибки второго рода β и в этом смысле ошибки первого и второго рода являются конкурирующими.

Значимость ошибок первого и второго рода может быть весьма различной и в одних случаях стремятся уменьшить α, в других – β. Применительно к радиолокации говорят, что α – вероятность пропуска сигнала, β – вероятность ложной тревоги, применительно к производству α – риск производителя (вероятность забраковать стандартные изделия), β – риск потребителя (вероятность пропустить нестандартные изделия).

Одновременное уменьшение ошибок первого и второго рода возможно лишь при увеличении объема выборок.

Обычно при проверке гипотезы задаются определенным уровнем значимости α и объемом выборки n. Критерий выбирается так, чтобы мощность критерия была максимальной.

11.5. Виды критических областей

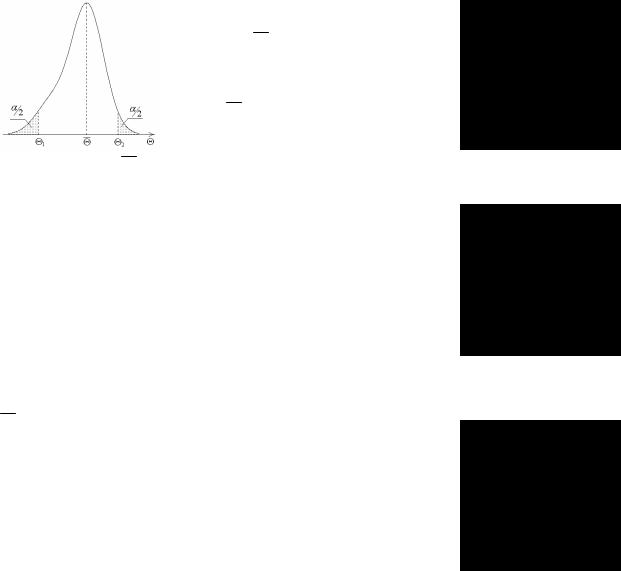
Пусть проверяется гипотеза о равенстве некоторого параметра генерального распределения, на-

пример генерального среднего X , данному числу a и для проверки гипотезы используется критерий Θ, распределение которого показано на рисунках. Если

верна нулевая гипотеза H0 : X = a , то M (Θ)= a . Если в качестве альтернативной гипотезы вы-

двигается H1 : X < a , то критическую область естественно определить неравенством Θ < Θ1 , т.е., выбрать левостороннюю критическую область. За-

альтернативная гипотеза формулируется в виде H1 :

X ≠ a , то строится двусторонняя критическая область, критические точки которой находятся из уравнения

Очевидно, две критические точки Θ1 и Θ2 из одного

уравнения можно найти бесчисленным количеством способов. Чаще всего двустороннюю критическую область строят как симметричную, определяя Θ1 и

указывается, относительно каких альтернатив должна быть произведена проверка, т.е. формулируется альтернативная гипотеза H1 .

3.Формулируется правило проверки, определяется соответствующий объем выборки n по заданным уровню значимости α и мощности критерия 1 – β или из условия минимизации β при данных α и n.

4.В зависимости от проверяемой гипотезы и ее альтернатив выбирается одноили двусторонняя проверка. Выбор альтернативной гипотезы

диктуется существом проверки. Если проверяется гипотеза, что процент брака составляет 5% (т.е. H0 : Θ = 0,05), то альтернативная гипотеза должна

формулироваться как H1 : Θ > 0,05, так как если процент брака меньше 5, то партия тем более должна быть принята. Если в гипотезе H0 : Θ=a Θ обозначает предел прочности материала на разрыв, то альтернативной гипотезой должна быть H1 : Θ< a . Наконец, если в гипотезе H0 : Θ=a Θ обозначает вес гири, то должна строиться двусторонняя критическая область Θ< Θ1 и

Θ> Θ2 .

5.По известному распределению критерия вычисляются критические точки.

Для каждого вида проверяемых гипотез разработаны соответствующие критерии. Чаще всего используются случайные величины, имеющие нор-

мальное распределение, распределение χ2 (Пирсона), t – распределение Стьюдента, F - распределение Фишера – Снедекора.

Приведенная выше схема предполагает, что закон распределения генеральной совокупности известен и оценке подлежат один или несколько параметров распределения. Такие гипотезы носят название параметрических. Наряду с подобными гипотезами приходится проводить статистические проверки и при неизвестном законе распределения генеральной совокупности. Соответствующие гипотезы называют

непараметрическими.

Непараметрические критерии обладают значительно меньшей мощностью, нежели параметрические, т.е. для сохранения той же величины β необходимо больше опытных данных. С другой стороны, непараметрические критерии могут применяться при любом законе распределения генеральной совокупности и применимы как к количественным, так и к качественным (ранговым) признакам.

12.1. Некоторые типичные задачи проверки параметрических гипотез

Рассмотрим некоторые наиболее часто встречающиеся задачи, решающиеся с помощью проверки гипотез. Это прежде всего задачи сравнения: сравнение выборочных характеристик (доли признака, среднего, дисперсии) с нормативными; сравнение характеристик двух выборок между собой (для проверки гипотезы о принадлежности этих выборок к одной генеральной совокупности). Типичные непараметрические задачи – проверка гипотезы о виде выборочного распределения, проверка значимости расхождения выборочных характеристик.

12.1.1. Проверка гипотез о доле признака а) Сравнение доли признака с нормативом

Пусть доля некоторого признака p в генеральной совокупности должна быть равной a , т.е., H0 : p = a . Рассмотрим вначале альтернативную гипотезу H1 : p ≠ a , т.е. двусторонний критерий проверки.

В качестве статистического критерия возьмем Θ= mn – частоту появле-

ния признака в выборке. Эта с.в. для возвратной выборки распределена по биномиальному закону, но при достаточно больших объемах выборки можно воспользоваться асимптотическими распределениями (Пуассона или нормальным). Для нормального распределения из уровня значимости α найдем

где Ф(z) – функция Лапласа. Среднеквадратическое отклонение для бино-

Для двустороннего критерия правило проверки выглядит следующим образом: если наблюдаемое значение критерия, вычисленное по данным выборки, попадает в интервал между критическими точками, Θ1 < Θнабл < Θ2 , нулевая

гипотеза p = a не отклоняется, если не попадает – отклоняется.

Рассмотрим односторонний критерий проверки, в качестве альтернативной

Изменение критерия может изменить результаты проверки.

Пример:

Пусть проводится проверка соответствия содержания активного вещества в продукции стандарту, который равен 10%, т.е. проверяется нулевая гипотеза H0 : p = 0,1, где p – доля активного вещества в продукции. Для контроля

произведена выборка из 100 проб, которая дала mn = 0,152 . Считать ли гипо-

тезу верной или продукцию следует забраковать как не соответствующую нормативам?

Решение:

Рассмотрим сначала случай, когда отклонения от норматива в обе стороны нежелательны, т.е. когда проверка производится по двустороннему критерию, H1 : p ≠ a . Примем уровень значимости α = 0,05 и по таблице функции

клоняется, партия продукции признается стандартной.

Пусть теперь недопустимым является только превышение нормативного содержания активного вещества, т.е. проверка должна быть произведена про-

наблюдаемое значение критерия попадает в критическую область и с тем же уровнем значимости нулевая гипотеза должна быть отклонена, партия продукции не соответствует стандарту.

б) Сравнение долей признака в двух совокупностях

купностях из n1 и n2 элементов. Нулевой гипотезой является предположение,

что обе совокупности представляют собой две выборки из одной генеральной совокупности с некоторой долей признака p , а расхождение выборочных

частот носит случайный характер. Построение статистического критерия различно для больших и малых выборок.

1. Большие выборки. Если n1 и n2 – большие числа (примерно больше 30), то распределение выборочных частот будет близко к нормальному с пара-

В данном случае необходимо использовать двусторонний критерий, т.е. аль-

где величина p заменяется ее точечной оценкой, полученной на основании данных двух выборок:

p = m1 + m2 . n1 + n2

Если наблюдаемое значение критерия, вычисленное по данным выборки, попадает в интервал между критическими точками, Θ1 < Θнабл < Θ2 , нулевая ги-

потеза не отклоняется, если не попадает – отклоняется.

Пример:

Пусть число бракованных изделий в экспериментальной партии составило 4 из 100, а в контрольной – 12 из 500.

Оценить с уровнем значимости α = 0,01 существенность расхождений долей брака в этих двух партиях.

Решение:

По уровню значимости α = 0,01 находим квантиль zα 2 = 2,58 .

Наблюдаемое значение Θнабл = 1004 − 50012 = 0,016 , т.е. лежит в допустимой

области. Таким образом, наблюдаемые различия не противоречат гипотезе H0 и полученное расхождение с уровнем значимости α = 0,01 можно счи-

тать несущественными.

2. Малые выборки. Если n1 и n2 – малые числа, то использование нормаль-

ного распределения для критерия Θ = m1 − m2 становится неправомерным. В n1 n2

этом случае используется критерий Пирсона χ2 . Вид соответствующей

плотности вероятности приведен в разделе, где обсуждались распределения, связанные с нормальным. Сгруппируем данные в таблицу.

Так как между четырьмя теоретическими частотами существуют три независимых соотношения, то независимой является только одна величина, т.е.

в распределении χ2 следует учесть одну степень свободы (ν =1).

Нулевую гипотезу формулируем в виде «обе совокупности есть выборки из одной генеральной совокупности». В данном случае естественно приме-