Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

vektor

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

4.59 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 188 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

лам двугранный угол, образованный двумя пересе-

2x y 3z 8 0

кающимися плоскостями: P1 : x 3y 2z 5 0 и

P2 : 3x 2 y z 3 0.

РЕШЕНИЕ:

n1 {1, 3,2}

{3,2, 1}:

Уравнение пучка плоскостей, проходящих через пря-

мую их пересечения:

x 3y 2z 5 3x 2y z 3 0 .

Выберем из них две, имеющие нормальные векторы,

параллельные n1 n2 {4, 1,1} и

{3, 2, 1} .

3 2

, откуда ,

положив 1, получаем уравнение первой плос-

кости в виде 4x 5y z 2 0;

3 2

, откуда , положив

1, получаем уравнение первой плоскости в виде

2x y 3z 8 0.

2. Прямая

Прямая L задана общими уравнениями

x y z 0,

L :

2x y 2 0.

Напишите канонические уравнения этой прямой и её

y 2

уравнения в виде проекций на координатные плоско-

сти.

z 2

РЕШЕНИЕ: Решим задачу двумя способами.

1-й способ

Найдем произвольную точку, лежащую на прямой,

3x 2

3y 2

предположив, что

x = 0, тогда из системы, задающей прямую двумя

уравнениями плоскости, найдем, что y = 2 и z = 2.

Точка M 0 (0,2,2) L . В качестве направляющего векто-

ра прямой можно выбрать вектор a n1 n2 , так как

3x z 2 0,

он будет перпендикулярен как n1

{1,1, 1}, так и

2x y 2 0,

n2 {2, 1,0}:

и канонические

3y 2z 2 0.

{ 1, 2, 3},

уравнения прямой принимают вид:

y 2

z 2

могут быть записаны в виде проекций на координат-

3x z 2 0,

ные плоскости следующим образом: 2x y 2 0,

3y 2z 2 0.

2-й способ

Из общих уравнений прямой L , исключая y и x в системе, получим уравнения прямой в проекциях на плоскости XOZ и YOZ:

		z	2
x					,
	3		3

	2z			2
y						.

3 3

Из этих уравнений z 3x 2

и z

3y 2

и канони-

ческие уравнения прямой можно записать в ви-

де

3x 2

3y 2

Докажите параллельность прямых

x 2

y 1

x y z 0,

L1 :

и L2 :

2 1

x y 5z 8 0.

РЕШЕНИЕ:

Направляющий вектор прямой L1 имеет вид:

a {3, 2,1}. Направляющий вектор прямой L2 может быть выбран в виде векторного произведения нормальных векторов двух пересекающихся плоскостей

n1	{1,1, 1}		и		n2 {1, 1, 5} :
				i	j	k
				1	1	1	{ 6,4, 2}.
a2	n1	n2		1	1	1	{ 6,4, 2}.
				1	1	5

Прямые L1 и L2 параллельны, так как компоненты их направляющих векторов пропорциональны:

l1 m1 n1 1 . l2 m2 n2 2

Определите угол между прямыми


L	:	x 3	y 2		z	и	L	2	:	x 2		y 3		z 5	.

1	1		1	2					1		1		2

РЕШЕНИЕ:

Угол между направляющими векторами прямых L1 и

определяется из значе-

L2 a1 {1, 1, 2} и

a2 {1,1, 2}

ния их скалярного произведения:

cos

l1l2 m1m2 n1n2

1 1 2

l12 m12 n12

l22 m22 n22

4 4

arccos

Найдите уравнения прямой, проходящей через точку

M (3,2, 1)

и пересекающей ось ox под прямым углом.

РЕШЕНИЕ:

Уравнение искомой прямой можно записать в виде

уравнения прямой, проходящей через две точки

M1 (x1 , y1 , z1 ) и M 2 (x2 , y2 , z2 ) :

x x1

y y1

z z1

. По условию M1 (3,2, 1).

x 3

y 2

z 1

x2 x1

z2 z1

y2 y1

Вторую точку находим из условия, что прямая пер-

пендикулярна оси ox и пересекает ее, то есть

M 2 (3,0,0), и уравнение искомой прямой принимает

вид:

x 3

y 2

z 1

Составьте параметрические уравнения прямой L, про-

ходящей через точку M 0 (2,0, 3) параллельно прямой

L :

x 1

y 2

z 1

РЕШЕНИЕ:

В качестве направляющего вектора искомой прямой L

x 5t 2,

можно взять направляющий вектор прямой L1

y 2t,

a a1 {5,2, 1}, так как прямые L и L1 параллельны по

z t 3.

условию; канонические уравнения прямой

L :

x 2

z 3

могут быть приведены к параметри-

ческому виду, если приравнять входящие в них отно-

шения значению параметра t:

x 5t 2,

y 2t,

z t 3.

Напишите канонические уравнения прямой L, прохо-

дящей через точку M 0 (2,0, 3) параллельно прямой

L1 :

3x y 2z 7 0,

x 3y 2z 3 0.

РЕШЕНИЕ:

Прямая L, параллельная прямой L1 , будет перпенди-

x 2

z 3

кулярна нормальным векторам

n1 {3, 1,2}

n2 {1,3, 2} плоскостей, образующих

прямую L1 , то есть

{ 4,8,10}, и канонические

уравнения прямой L принимают вид:

x 2

z 3

Определите, при каком значении l

прямые

L :

x 2

z 1

x 3

y 1

z 7

пересе-

каются.

РЕШЕНИЕ 1:

По условию прямая L1 проходит через точку

M1 ( 2,0,1) , а прямая L2

- через точку M 2 (3,1,7) .

Условием пересечения двух прямых будет условие

компланарности векторов M

, которое мож-

2 M1 , a1 , a2

но записать в виде:

x2 x1

y2 y1

z2 z1

2 M1 a1

то есть

22l 66 0,

откуда

l 3.

РЕШЕНИЕ 2:

3x 6 2y

Решим систему

2x 4 z 1

. Получаем

4z 28

2y 2

x 0, y 3,z 5. Подставим в последнее уравне-

ние с l:

3 1

l 3.

Составьте уравнение прямой, проходящей через точку

(1,1,1) , пересекающей прямую

и пер-

пендикулярную прямой L2 :

x 1

y 2

z 3

РЕШЕНИЕ 1:

x 1

y 1

z 1

Уравнение искомой прямой L :

. Она

x 1

y 1

z 1

лежит в одной плоскости с прямой L1 , проходящей

2 5

через точку M 2 (0,0,0) , то есть

l 2m n 0,

и перпендику-

2 M1 a1

лярна прямой L2 с направляющим вектором

{2,1, 4} . Условие перпендикулярности прямых за-

ключается в равенстве (a1 a2 ) 0 2l m 4n 0. Ре-

l 2m n 0

шим систему для определения

2l m 4n 0

l, m и n. Выражая l и m через n , найдем

l 2m n,

2l m 4n,

l n 2m,	при m	2	n,	l	9	n, та-


5m 2n,	5			5

ким образом,

l : m : n 9 : 2 : ( 5)

и уравнение искомой

прямой L имеет вид:

x 1

y 1

z 1

РЕШЕНИЕ 2:

x 1 t

Рассмотрим пучок прямых: y 1 t . Из условия

перпендикулярности имеем

z 1 t

2 4 0 2 4 . Условие пересечения

даёт систему:

1 t

,t 0, или

2 2 t 1 t 1 2 2 t

Из системы следует

3 3 t 1 t

. Таким образом, в качестве

16t

направляющего вектора можно взять вектор

9, 2,5 .

x 1

y 1

z 1

3. Прямая и плоскость

Найдите точку пересечения прямой L :

x 1

y 1

плоскости P : 2x 3y z 1 0.

2 6

РЕШЕНИЕ:

Для определения координат точки пересечения запи-

шем уравнения прямой L в параметрическом виде:

(2,-3,6)

x 1 t,

y 1 2t, z 6t . Подставляя эти выражения в

уравнение плоскости Р, получим уравнение для опре-

деления значения параметра t, соответствующего точ-

ке их пересечения:

2(t 1) 3( 2t 1) 6t 1 0 t 1, следовательно, коор-

динаты искомой точки x 2,

y 3,

z 6.

Составьте уравнение плоскости Р, проходящей через

4x 6y 5z 1

данную прямую L и точку

M 0 (2, 2,1) , если прямая

x 2t 1,

L : y 3t 2, задана параметрическими уравнения-

z 2t 3,

ми. РЕШЕНИЕ 1:

Перейдем к каноническим уравнениям прямой

L : x 1 y 2 z 3 . Чтобы записать уравнение пучка

плоскостей, проходящих через прямую L, и выбрать из него искомую плоскость, проходящую через точку M 0 , составим уравнение прямой L в виде ее проекций на плоскости XOY и XOZ. Из канонических уравнений получим

3(x 1) 2( y 2)		3x 2y 7 0
L :	2(x 1) 2(z 3)		x z 4 0.

Уравнение пучка плоскостей через прямую L имеет вид:

(x z 4) (3x 2 y 7) 0 (1 3 )x 2 y z (4 7 ) 0.

Так как плоскость проходит через точку M 0 , подставим ее координаты в уравнение пучка плоскостей и найдем значение , определяющее искомую плос-

кость 2 6 4 1 4 7 0

, и уравнение

плоскости Р будет иметь вид: 4x 6 y 5z 1 0.

РЕШЕНИЕ 2:

x 2t 1,

две точки, например,

Найдем на прямой L : y 3t 2,

z 2t 3

t1 0 и t2

0 , откуда M1 (1, 2, 3) L и M2 (3, 1, 1) L .

Из уравнения плоскости, проходящей через три точки

M0 , M1 , M2 , получаем

P :

x 2

y 2

z 1

0 4x 6y 5z 1 0.

Составьте уравнение плоскости, проходящей через

прямую

3x 2y 5z 6 0,

L1 :

параллельно прямой

x 4 y 3z 4 0,

2x 3y 4z 5

L2 :

x 1

y 5

z 1

РЕШЕНИЕ 1:

n {3 ,2 4 ,5 3 }

Запишем уравнение пучка плоскостей, проходящих через прямую L1 :

3x 2y 5z 6 (x 4 y 3z 4) 0

(3 )x (2 4 )y (5 3 )z (6 4 ) 0.

Выберем из всех плоскостей с нормальными векторами ту, которая параллельна направляющему вектору прямой L2 , равному

a2 {3,2, 3}. Нормальный вектор плоскости n , перпендикулярен a2 и удовлетворяет условию (n a2 ) 0 :

3(3 ) 2(2 4 ) 3(5 3 ) 0 . Из этого уравнения находим значение 1 , при котором уравнение искомой плоскости принимает вид:

2x 3y 4z 5 0 .

РЕШЕНИЕ 2:

Найдем нормальный вектор искомой плоскости как векторное произведение направляющих векторов прямых.

a2 {3,2, 3};

	i	j	k	{ 14, 4,10} {7, 2, 5};
a1	3	2	5	{ 14, 4,10} {7, 2, 5};
	1	4	3

	i	j	k	{ 4, 6, 8} {2,3, 4}.
n 3		2	3	{ 4, 6, 8} {2,3, 4}.
	7	2	5

Найдем произвольную точку на

3x 2 y 5z 6 0,

L1 :

x 4y 3z 4 0.

Положим x 0 ,

2y 5z 6,

найдем

из

4y 3z 4,

M0 (0,

) . Уравнение плоскости с нормальным

вектором n , проходящей через точку M0 , имеет

вид:

2(x 0) 3( y

) 4(z

) 0 2x 3y 4z 5 0.

Составьте уравнение плоскости Р, проходящей через

прямую L :

x 1

z 1

перпендикулярно к плоско-

сти

3x y 2z 1 0

P1 : x y z 1 0,

L P.

РЕШЕНИЕ:

Уравнение прямой L в проекциях:		2x 2 0,
Уравнение прямой L в проекциях:
	y 2z 2 0.

Уравнение пучка плоскостей, проходящих через прямую L, имеет вид:

(2x 2) y 2z 2) 0 2x y 2 z 2( 1) 0

с общим нормальным вектором n {2, , 2 }, зависящим от параметра .

Условие перпендикулярности искомой плоскости и плоскости P1 с n1 {1,1, 1} имеет вид:

(n n ) 2 2 0	и дает значение	2	, при кото-

1	3

ром получается уравнение плоскости Р в виде

3x y 2z 1 0.

Найдите уравнения проекции прямой L : x 1 y 1 z

на плоскость

P : x y 2z 5 0.

РЕШЕНИЕ:

Запишем уравнение пучка плоскостей, проходящих

через прямую L, уравнение которой в проекциях име-

ет вид:

2x y 3 0, (2x y 3) (3x z 3) 0

(2 3 )x y z 3(1 ) 0.

3x z 3 0,

Плоскость P1

из этого пучка, проектирующая эту

прямую L на плоскость Р, определится из условия

перпендикулярности этих плоскостей с нормальными

векторами n1 {(2 3 ), 1, } и

n {1,1,2};

(n1 n) 1(2 3 ) 1( 1) 2( ) 0,

откуда 1.

При этом значении получаем уравнение проекти-

рующей плоскости P1 : x y z 0 , а проекцией прямой

L на плоскость Р будет линия пересечения двух плос-

костей

x y 2z 5 0

Lпр :

или в каноническом виде:

x y z 0,

Lпр :

Найдите проекцию точки M (5,2, 1) на плоскость

P : 2x y 3z 23 0.

РЕШЕНИЕ 1:

(1,4,-7)

Проекцией точки M на плос-

кость Р будет точка пересечения

прямой L, проходящей через

точку М перпендикулярно к плоскости Р. Уравнение перпендикуляра через точку М будет иметь вид:


L :	x 5	y 2	z 1		t и координаты проекции M				ďđ

2		1		3
найдем, подставив x 2t 5,						y t 2,	z 3t 1
в уравнение плоскости Р:								t 2 и
2(2t 5) t 2 3(3t 1) 23 0, откуда
xďđ 1,		yďđ 4,			zďđ 7.

РЕШЕНИЕ 2:

Координаты точки проекции можно найти непосред-

							x 5		y 2		z 1

								2	1
ственно решая систему								2	1	3 .
								2x y 3z 23 0
								2x y 3z 23 0

Найдите:
1) проекцию точки M (0,1,2) на пря-
мую L :	x 1		y		z 1	,	M L ,
мую L :						,	M L ,
2		1		0

2)расстояние от точки M (0,1,2) до этой прямой,

3)запишите уравнение перпендикуляра L1 из точки

	M (0,1,2) на прямую L :							x 1					y						z 1		,
	M (0,1,2) на прямую L :																				,
									2					1						0
	4) найдите точку N , симметричную точке M (0,1,2) от-
	носительно прямой L :								x 1						y					z 1		.				3 1
																							O				,			, 1
									2					1						0			O				,			, 1
	РЕШЕНИЕ:								2					1						0						5		5
	РЕШЕНИЕ:																								270
	1). Из условия n {2,1,0}. Уравнение плоскости Р,
27	1). Из условия n {2,1,0}. Уравнение плоскости Р,																							5
27	перпендикулярной к прямой L и проходящей через																							5
	перпендикулярной к прямой L и проходящей через																						x 1						y		z 1
	точку M, имеет вид:																														0
	точку M, имеет вид:																							2				1			0
	2x 1( y 1) 0(z 2) 0 2x y 1 0																						6			,		7	, 4
	координаты точки пересечения этой плоскости с пря-
																								5				5
																								5				5
	мой L : x 1 2t,					y t,				z 1							находим из уравнения
	2(2t 1) t 1 0 t						1			. Координаты точки пересече-
	2(2t 1) t 1 0 t									. Координаты точки пересече-
						5
	ния прямой и плоскости дадут координаты проекции
	точки М на плоскость										3					1
										O		,						, 1 .
										O	5	,				5		, 1 .
											5					5
	2). Способ 1. Искомое расстояние равно расстоянию
	между точкой M (0,1,2)								и ее проекцией на прямую –
		3		1
	точкой O		,		, 1 :
	точкой O		,	5	, 1 :
		5		5

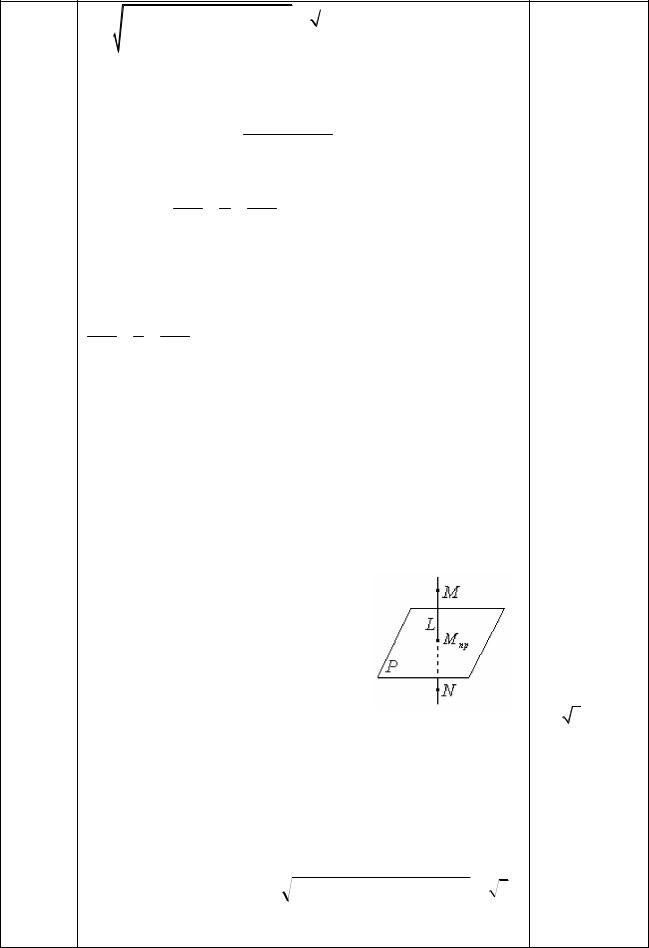
d	3	2		1	2		2	270	.
			1			(2 1)
	5		1	5		(2 1)		5
	5			5				5

Способ 2. Расстояние от точки до прямой можно най-


	M 0M q
ти по формуле: d			.


		q

3). Уравнение перпендикуляра L1 из точки M (0,1,2) на прямую L : x 1 y z 1 напишем как уравнение пря-

						2		1		0
мой, проходящей через две точки M (0,1,2)																	и
O	3	,	1	, 1	:	L :	x 0				y 1			z 2	,	x	y 1		z 2	,
O		,		, 1	:	L :									,					,
	5	5						3	0			1	1	1 2		1	2	5
								5	0			5	1
								5				5

x 1 y z 1 .

2 1 0

4). Для того чтобы найти координаты точки N, заметим, что точка О делит отрезок MN пополам и

	x	xM xN					,		y			yM yN					,	z	0		zM zN								,
	x						,		y								,	z											,
	0		2							0	2												2
	откуда		x			6		, y					7	, z		4		и			6			7				.
																					6			7
				N					N						N					N		,				,
				N		5			N		5				N					N		,				,	4
						5					5										5			5
	Найдите:
	1) расстояние от точки M (1,1,1) до плоскости
					P : x y 2z 6 0 ,
	2) координаты точки N, симмет-
	ричной точке M (1,1,1)										относитель-
	но плоскости P : x y 2z 6 0.
	РЕШЕНИЕ:
	1). Способ 1. Уравнение прямой,
	проходящей через точку M (1,1,1) ,																																,
28	перпендикулярно к плоскости Р с																															6	,
	n {1,1, 2} , можно записать в виде L :																			x 1					y 1					z 1	(3,3, 3)
																				x 1					y 1					z 1	.
																															.
																				1				1						2
	Проекцию точки М на плоскость Р находим как точку
	пересечения						прямой					L : x t 1,						y t 1,							z 2t 1
	и плоскости							P : t 1 t 1 2( 2t 1) 6 0 ,																					откуда

t 1 и O 2,2, 1 .

Искомое расстояние d (2 1)2 (2 1)2 ( 1 1)2 6 . Способ 2. Расстояние находим по известной формуле (см. задачу № 11)

<<< < Предыдущая 1 2 3 4 5 6 78 / 188 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.201531.13 Кб14Variant_11.docx
#
29.04.2019436.53 Кб8Vasiliy A Ecology.docx
#
22.02.201522.46 Mб129VDISCHARGE.doc
#
23.02.201510.15 Mб87VDISCHARGE1.pdf
#
22.02.201579.75 Кб5VEDAR.docx
#
23.02.20154.59 Mб10vektor.pdf
#
23.02.2015284.99 Кб2Vektory2lekts.pdf
#
22.02.2015815.62 Кб6Verian10.doc
#
22.02.2015387.07 Кб4Verian11.doc
#
22.02.2015698.88 Кб4Verian12.doc
#
22.02.2015686.59 Кб4Verian13.doc