2.4. Невырожденные системы n линейных уравнений с n неизвестными

Звуковое сопровождение лекции

Рассмотрим систему

(*)

Обозначим

– –столбец неизвестных,

– – матрица коэффициентов перед­неизвестными,

– –столбец свободных членов.

Тогда система уравнений (*) может быть записана в форме матричного уравнения

. (**)

Если , существует и единственно решение матричного уравнения (**)

, (1)

или в поэлементной записи

(2)

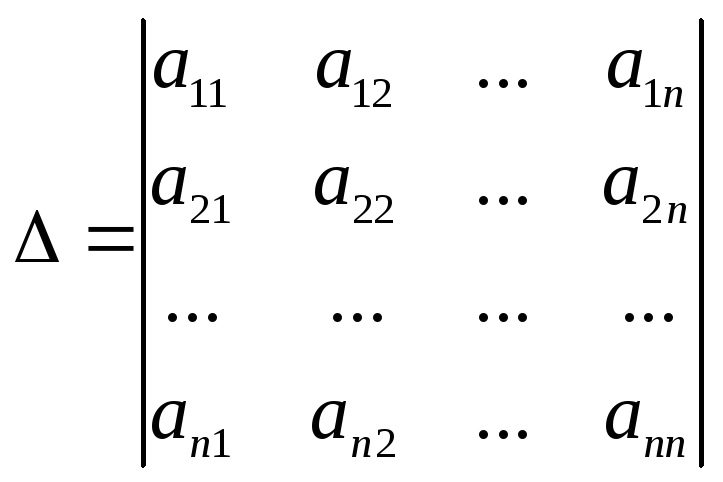
где – главный определитель системы;– определитель, полученный из главного путем замены-го столбца столбцом свободных членов (формулы (2) называютсяформулами Крамера).

Подробнее

, .

Вывод

Если главный определитель системы линейных уравнений снеизвестными отличен от нуля, то существует и единственно решение такой системы. Оно может быть найдено одним из трех способов:

1) матричным способом;

2) по формулам Крамера;

3) методом Гаусса (приведение системы к треугольному виду).

Алгоритм реализации последнего совпадает с алгоритмом приведения определителя к треугольному виду.

Пример

Решите систему линейных уравнений используя формулы Крамера.

Решение

По формулам Крамера ,,и .

Пример12 (для самопроверки)

Решите систему линейных уравнений, используя формулы Крамера:

Ответ

Пример

Решите систему линейных уравнений, используя метод Гаусса

Решение

Запишем расширенную матрицу системы и воспользуемся примером, рассмотренным в пункте 1.5:

1 действие. В качестве рабочей строки выберем первую строку, затем, пользуясь 7 свойством определителей, сложим первую строку, умноженную на -1 с остальными тремя строками.

2 действие. В качестве рабочей строки выберем вторую строку, затем, сложим вторую строку, умноженную на -2 с третьей строкой и сложим ее, умноженную на -3, с четвертой строкой.

3 действие. В качестве рабочей строки – третью, затем умножим ее на -3 и прибавим к четвертой строке. Таким образом, мы привели определитель к треугольному виду и можем легко вычислить его.

Восстановим по матрице систему полученных уравнений:

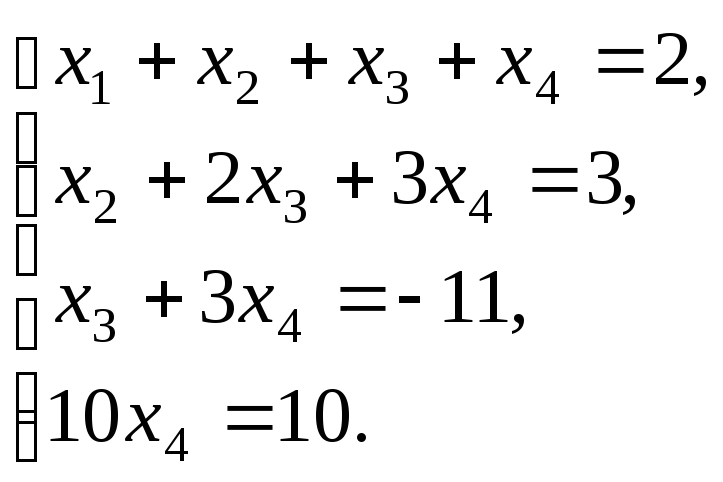
Из системы видно, что

Пример 13 (для самопроверки)

Решите систему линейных уравнений, используя метод Гаусса:

Ответ

2.5. Задания для самопроверки

Открыть задания

Ответы к примерам для самопроверки

1.

2.

3.

4. ,

5.

6.

7.

8.

9.

10.

11.

12.

13.

31