1.5. Вычисление определителей n-го порядка (2 метода)

Звуковое сопровождение лекции

I. Понижение порядка по свойству 8 (формулы разложения).

II. Приведение определителя к треугольному виду (алгоритм на основе свойства 7).

Пример

Вычислите определитель 4-го порядка 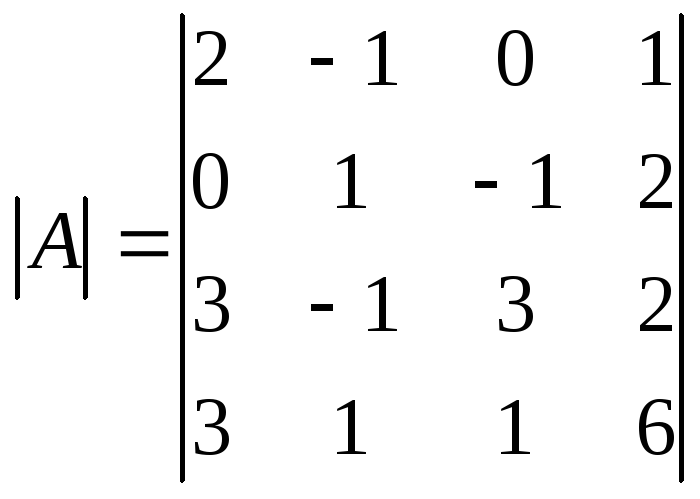методом понижения порядка.

Решение

Для разложения определителя по элементам строки или столбца выгодно использовать строку или столбец, в котором есть нули. Таковыми являются, например, вторая строка и третий столбец. Увеличим количество нулей в первой строке, для чего сложим второй и четвертый столбцы.

.

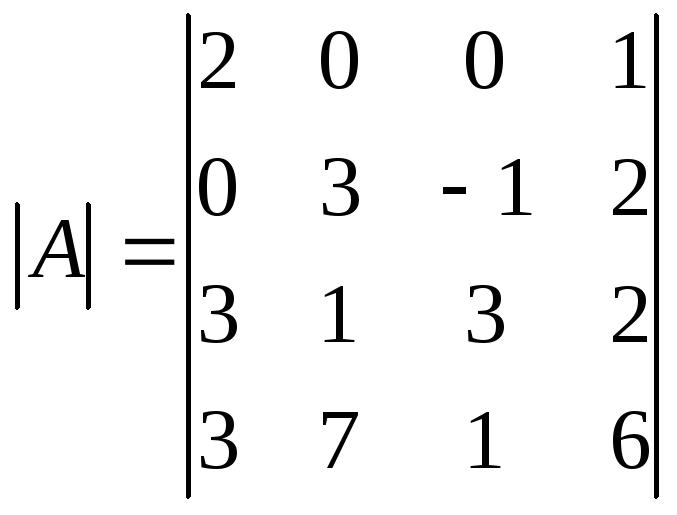Этот определитель разложим по элементам первой строки.

.

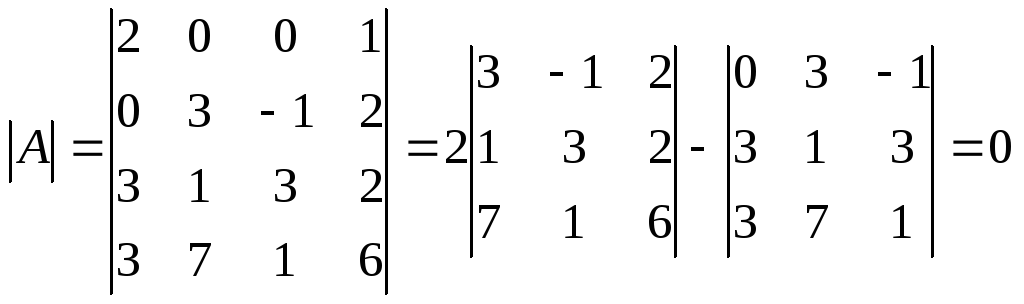Пример

Вычислите определитель 4-го порядка методом приведения к треугольному виду.

Решение

1 действие. Для того чтобы вычислить определитель методом приведения к треугольному виду получим нули в первом столбце, за исключением первой строки. Для этого в качестве рабочей строки выберем первую строку, затем, пользуясь 7 свойством определителей, сложим первую строку, умноженную на -1 с остальными тремя строками.

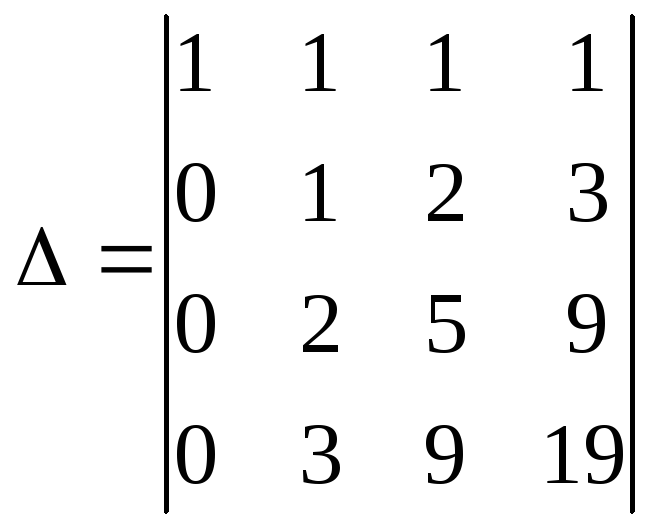
2 действие. Теперь получим нули во втором столбце в третьей и четвертой строке. Для этого в качестве рабочей строки выберем вторую строку, затем, сложим вторую строку, умноженную на -2 с третьей строкой и сложим ее, умноженную на -3, с четвертой строкой.

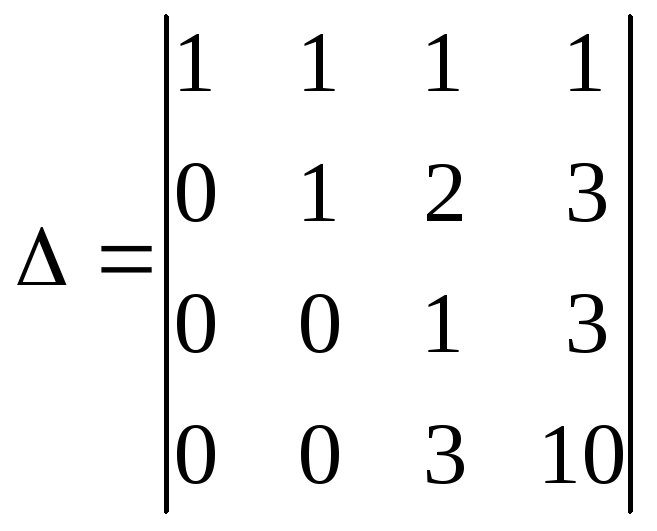
3 действие. Аналогично получим ноль в третьем столбце, выбрав в качестве рабочей строки – третью, затем умножим ее на -3 и прибавим к четвертой строке. Таким образом, мы привели определитель к треугольному виду и можем легко вычислить его.

Пример 5(для самопроверки)

Вычислите определитель 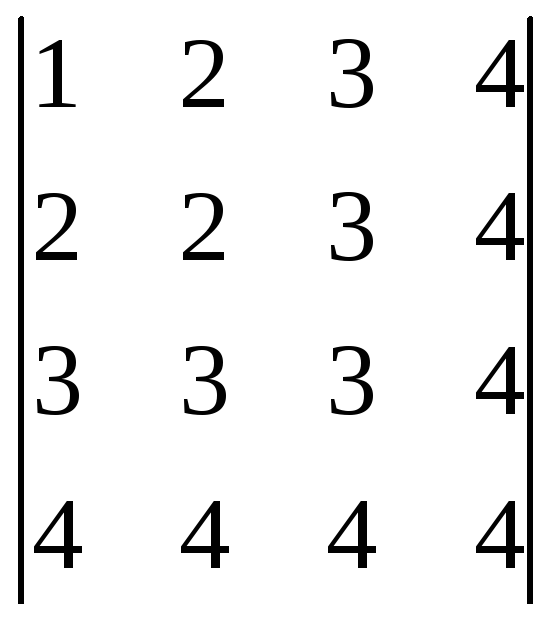двумя способами.

Ответ

Пример 6(для самопроверки)

Вычислите определитель 5-го порядка .

Ответ

1.6. Задания для самопроверки

Открыть задания

Лекция 2. Алгебра матриц

Содержание

1. Основные операции над матрицами и их свойства.

2. Обратная матрица.

3. Решение матричных уравнений.

4. Невырожденные системы n линейных уравнений с n неизвестными.

5. Задания для самопроверки

Определения	Теоремы и свойства
вырожденная матрица невырожденная матрица нулевая матрица обратная матрица перестановочная матрица равенство матриц сложение матриц умножение матриц умножение матрицы на число	правило умножения матриц свойства операции сложения свойства операций умножения матрицы на число и умножения матриц теорема о существовании и единственности обратной матрицы формулы Крамера

2.1. Основные операции над матрицами и их свойства

Звуковое сопровождение лекции

Определим несколько отношений и операций над матрицами.

Рассмотрим матрицы размера,–.

Равенство матриц

, ,…;,…

Сложение матриц

Результатом сложения матриц и называется матрица, элементы которой являются суммой соответствующих элементов исходных матриц.

Умножение матрицы на число

Умножение матриц

Пусть размера,–,

тогда их произведением называется матрица размера :

.

Правило умножения матриц

1. Перемножать можно лишь матрицы согласованных размеров (число столбцов матрицы равно числу строк матрицы).

2. Размер матрицы равен произведению числа строк матрицына число столбцов матрицы, т.е..

3. Чтобы получить элемент матрицы произведения , расположенный на пересечении-й строки и-го столбца следует перемножить соответствующие элементы-й строки матрицыи-го столбца матрицыи найти сумму полученных произведений.

Пример

, .

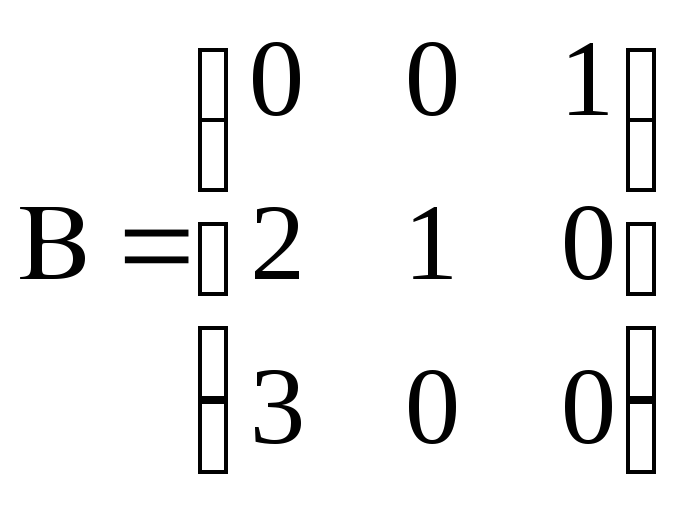1. .

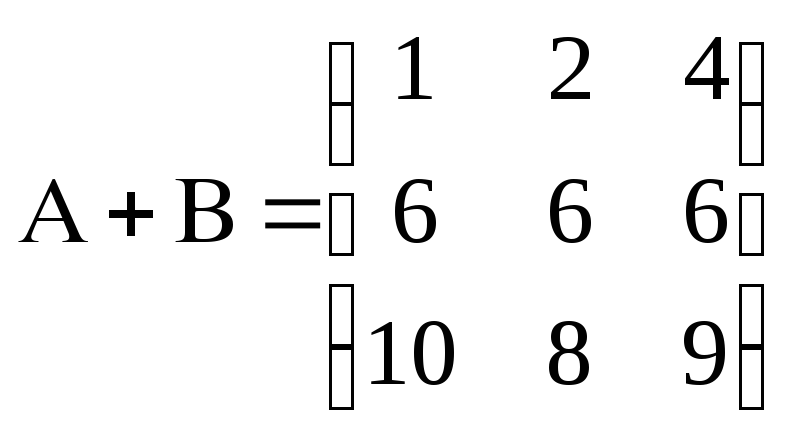2. .

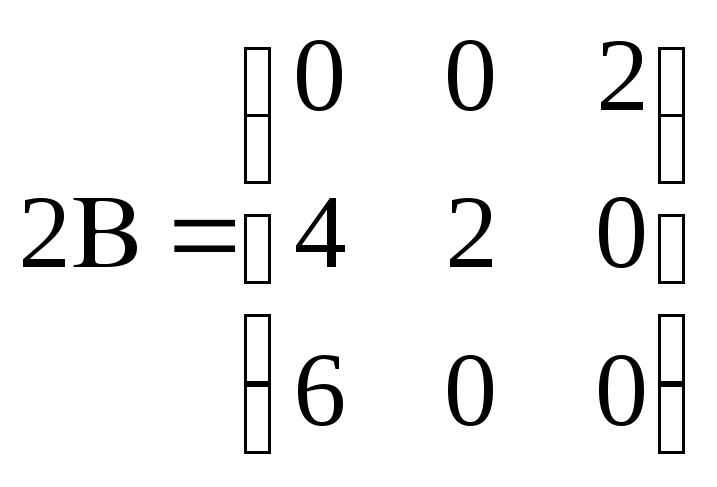3. ,–.

,

,

…

.

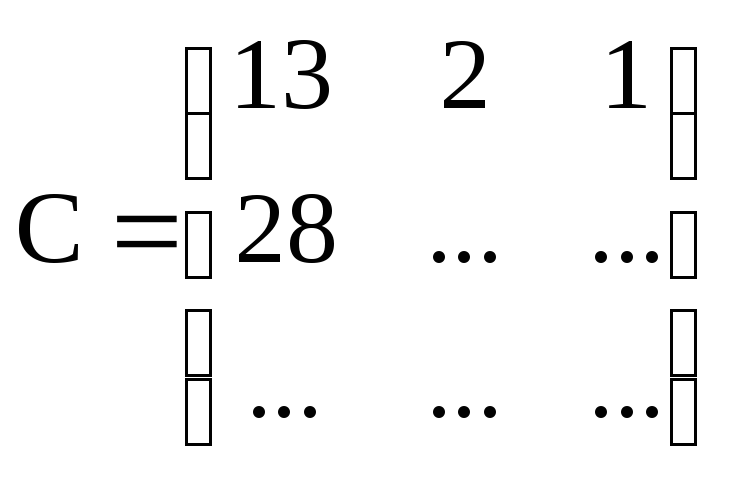Пример 7(для самопроверки)

Найдите .

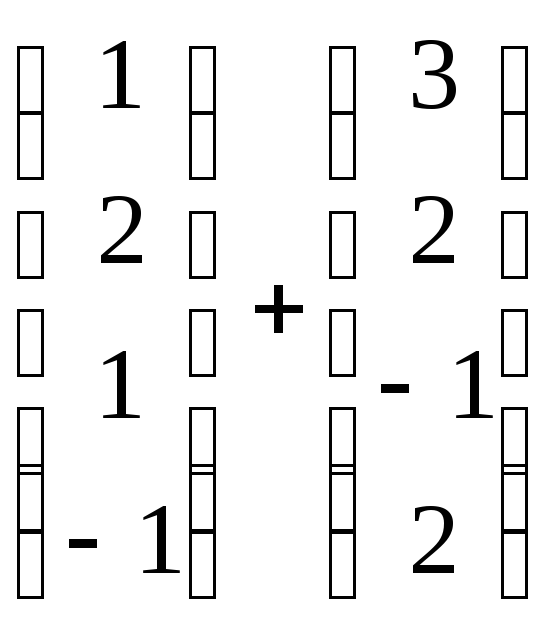Ответ

Пример8( для самопроверки)

Найдите , если .

Ответ

Пример 9(для самопроверки)

Найдите , если .

Ответ