- •Предел и непрерывность функции одной переменной
- •2. Окрестности конечной точки и бесконечности
- •3. Определение предела функции
- •3.1. Предел функции на языке окрестностей
- •Если для такое, чтодля3.2. Предел функции на языке неравенств
- •3.3. Предел последовательности
- •5. Бесконечно малые функции
- •5.1. Определение и основные свойства
- •5.2. Отношение бесконечно малых. Неопределенность
- •5.3. Первый замечательный предел
- •5.4. Сравнение бесконечно малых
- •6. Бесконечно большие функции
- •6.1. Определение и основные свойства
- •6.2. Неопределенности
- •6.3. Неопределенность . Второй замечательный предел
- •7. Непрерывные функции
- •7.1. Функции, непрерывные в точке
- •7.2. Точки разрыва функции и их классификация
- •7.3. Функции, непрерывные на отрезке
- •Дифференциальное исчисление функции
- •Дифференцируемые функции. Дифференциал
- •8.4. Связь между непрерывностью и дифференцируемостью
- •8.5. Производная суммы, произведения, частного
- •8.6. Производная сложной функции
- •8.7. Логарифмическое дифференцирование
- •8.13. Дифференциалы высших порядков
- •9.2. Правило Лопиталя
- •9.3. Формула Тейлора
- •9.4. Асимптотические разложения
- •10.3. Наибольшее и наименьшее значение функции на отрезке
- •10.4. Выпуклость и вогнутость. Точки перегиба
- •10.5. Асимптоты графика функции
- •Свойства неопределенного интеграла
- •13. Основные методы интегрирования
- •13.1. Метод подведения под знак дифференциала
- •Метод замены переменной
- •Метод интегрирования по частям
- •14. Интегрирование некоторых классов функций
- •14.2. Интегрирование функций, содержащих квадратный трехчлен
- •14.3. Интегрирование дробно-рациональных функций
5. Бесконечно малые функции
5.1. Определение и основные свойства
|
Функция
|
Рассмотрим ряд свойств бесконечно малых функций.
|
Теорема 5.1 (о связи функции с ее конечным пределом).
|
Теорема 5.2 (о произведении бесконечно малой функции на ограниченную).
Пусть
функция
![]() − бесконечно малая при
− бесконечно малая при![]() ,
а функция
,
а функция![]() − ограничена в некоторой выколотой
окрестности точки
− ограничена в некоторой выколотой
окрестности точки![]() .
Тогда произведение этих функций
.
Тогда произведение этих функций![]() является бесконечно малой функцией при
является бесконечно малой функцией при![]()
Теорема 5.3 (о сумме, разности, произведении бесконечно малых).
Сумма,
разность, произведение конечного числа
бесконечно малых функций при
![]() есть функция бесконечно малая при
есть функция бесконечно малая при![]() .
.
5.2. Отношение бесконечно малых. Неопределенность
В
отличие от суммы и произведения, отношение
бесконечно малых функций может иметь
любой предел или даже его не иметь.
Например, для функций
![]() ,
являющихся бесконечно малыми при
,
являющихся бесконечно малыми при![]() ,
имеем:
,
имеем:
![]() ,
,
![]()
![]()
Поэтому
отношение бесконечно малых функций
называют неопределенностью вида
![]() .
Отыскание предела в случае неопределенности
называют раскрытием неопределенности.
.
Отыскание предела в случае неопределенности
называют раскрытием неопределенности.
5.3. Первый замечательный предел
При
вычислении пределов выражений, содержащих
тригонометрические функции, часто
используется
![]() Он является неопределенностью
Он является неопределенностью![]() .
.
Покажем, что
![]() .
(5.1)
.
(5.1)
Это равенство называют первым замечательным пределом.
Следствие:
![]()
5.4. Сравнение бесконечно малых
Бесконечно
малые функции часто сравнивают между
собой по «быстроте» стремления к нулю.
Так, например, из двух функций
![]() и
и![]() − бесконечно малых при
− бесконечно малых при![]() ,
функция
,
функция![]() стремится к нулю «быстрее», чем
стремится к нулю «быстрее», чем![]() .
Уточним, какой смысл вкладывается в
слово «быстрее».
.
Уточним, какой смысл вкладывается в
слово «быстрее».
Пусть
![]() и
и![]() бесконечно
малые функции при
бесконечно
малые функции при![]() .
.
Если
 конечен и отличен от нуля, то
конечен и отличен от нуля, то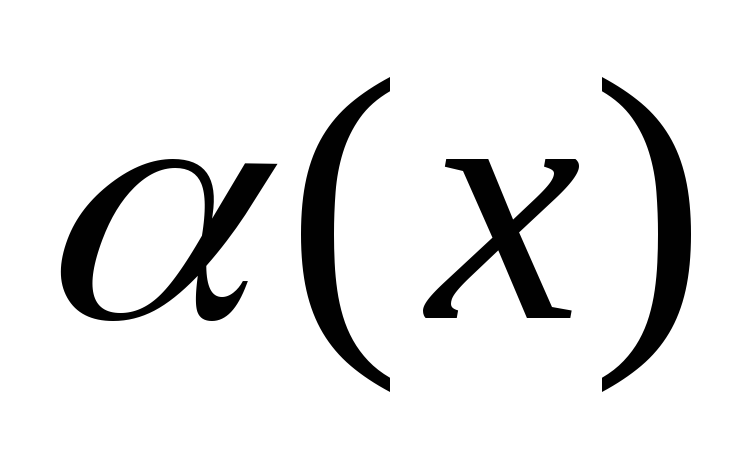 и
и называют
бесконечно малымиодного порядкаи обозначают так:
называют
бесконечно малымиодного порядкаи обозначают так: при
при .
.
В
частности, если
![]() то
то![]() и
и![]() называютэквивалентными бесконечно
малыми и обозначают так:
называютэквивалентными бесконечно
малыми и обозначают так:![]()
![]() при
при![]() .
.
Если
 то
то называют бесконечно малойболее
высокого порядка, чем
называют бесконечно малойболее
высокого порядка, чем и обозначают так:
и обозначают так: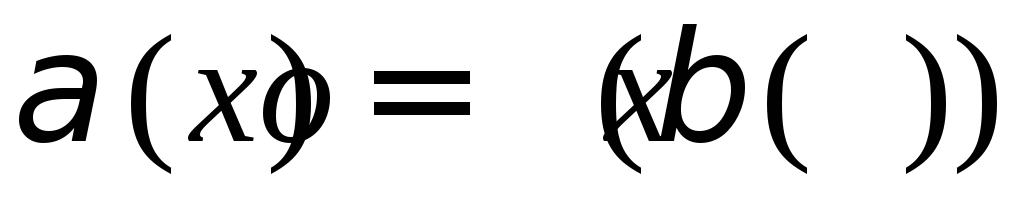 при
при .
.Если
 то
то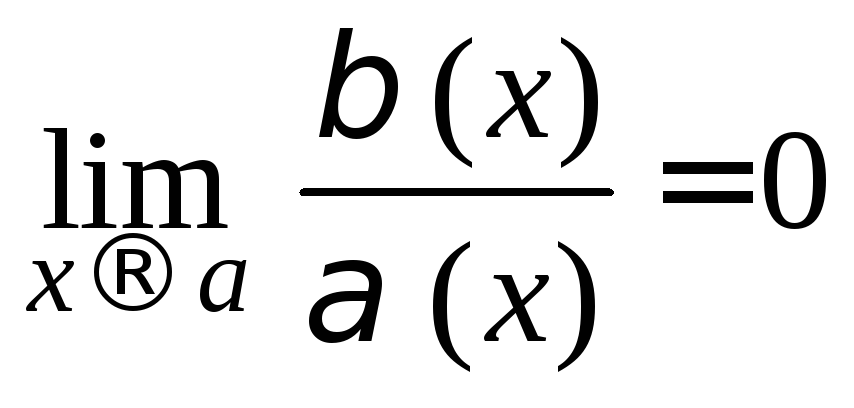 и
и будет бесконечно малой более
будет бесконечно малой более
высокого
порядка, чем
![]() при
при![]() .
.
Если
 не существует, то
не существует, то и
и называютнесравнимыми бесконечно
малыми при
называютнесравнимыми бесконечно
малыми при .
.
|
|
Это вытекает из первого замечательного предела и его следствия.
|
Теорема 5.4 (об эквивалентных бесконечно малых).
Пусть
|
6. Бесконечно большие функции
6.1. Определение и основные свойства
|
Функция
|
Различают
частные случаи бесконечно больших
функций, когда
![]() или
или![]() .
.
Рассмотрим некоторые свойства бесконечно больших функций.
Теорема 6.1 (о связи с бесконечно малой).
Если
функция
![]() бесконечно
большая при
бесконечно
большая при![]() ,
то функция
,
то функция![]() бесконечно
малая при
бесконечно
малая при![]() .
.
Если
функция
![]() бесконечно
малая при
бесконечно
малая при![]() и
и![]() в выколотой окрестности точки
в выколотой окрестности точки![]() ,
то функция
,
то функция![]() бесконечно
большая при
бесконечно
большая при![]() .
.
.
Теорема 6.2 (об арифметических операциях).
1).
Произведение двух бесконечно больших
при
![]() есть бесконечно большая при
есть бесконечно большая при![]() .
.
2).
Произведение бесконечно большой при
![]() на функцию, имеющую ненулевой предел
при
на функцию, имеющую ненулевой предел
при![]() ,
есть бесконечно большая при
,
есть бесконечно большая при![]() .
.
3).
Отношение бесконечно большой при
![]() к бесконечно малой (отличной от нуля)
при
к бесконечно малой (отличной от нуля)
при![]() есть бесконечно большая при
есть бесконечно большая при![]() .
.
4).
Сумма двух бесконечно больших одного
знака при
![]() есть бесконечно большая того же знака
при
есть бесконечно большая того же знака
при![]() .
.