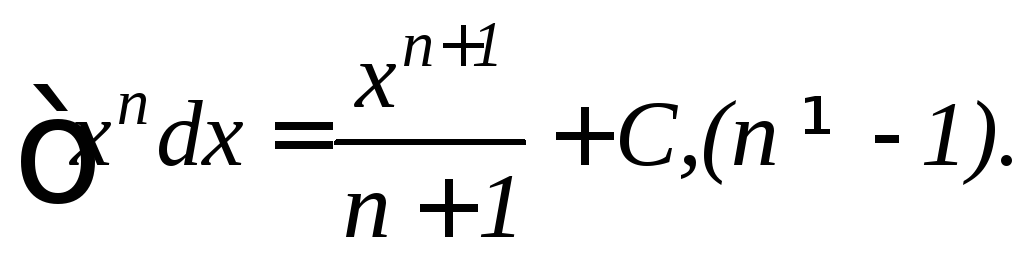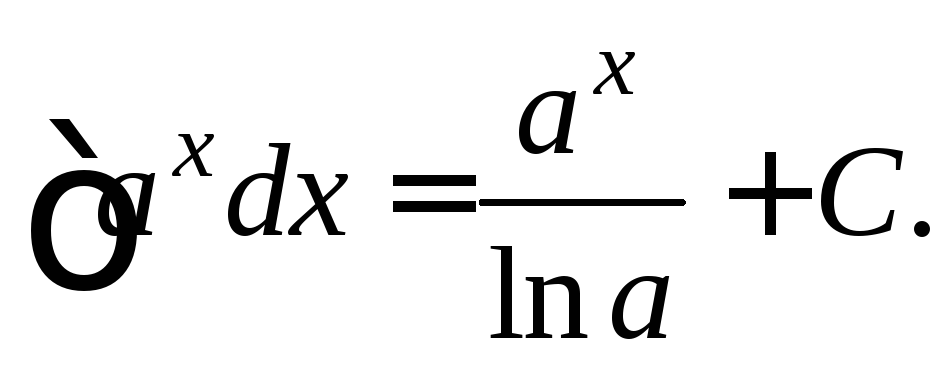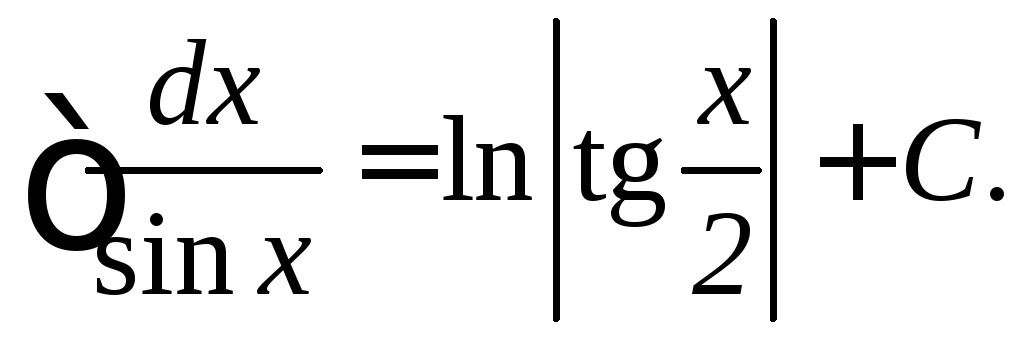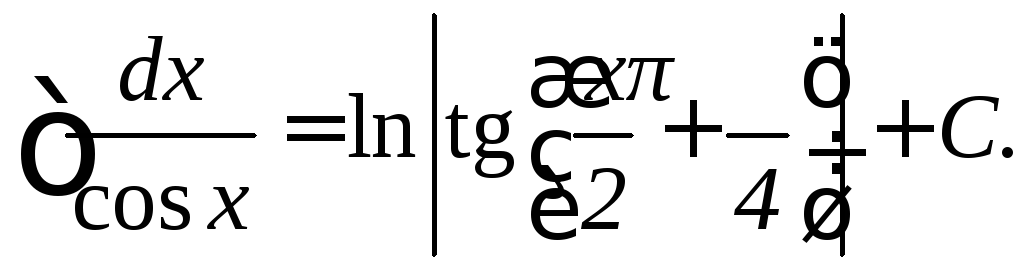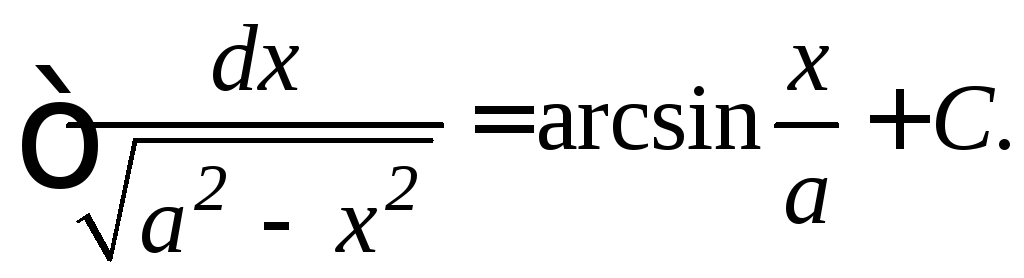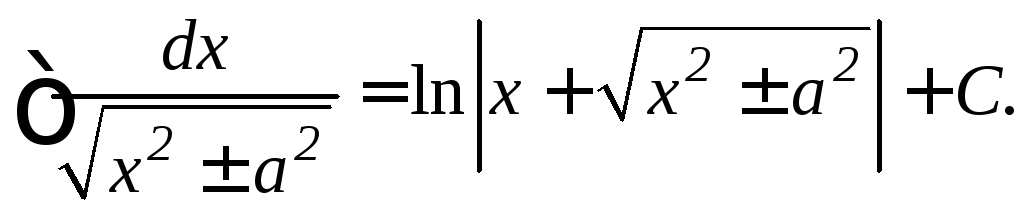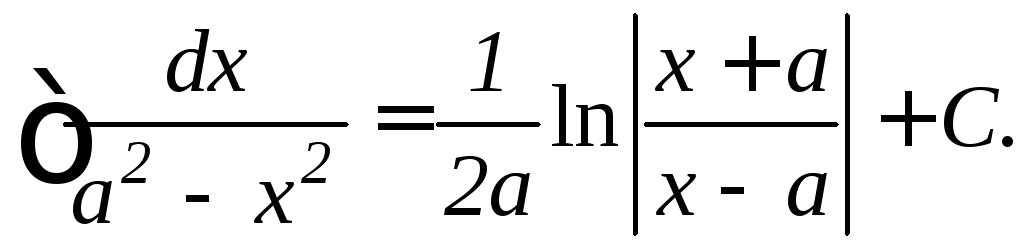8. Неопределенный интеграл
8.1. Первообразная и неопределенный интеграл
Функция F(x)
называетсяпервообразнойфункцииf(x)на(a; b),еслиF'(x)
= f(x)для любого![]() .
.
Если F(x) иФ(x) две первообразные функцииf(x), тоФ(x) = F(x) + C, т.е. две любые первообразные одной и той же функции отличаются на постоянную величинуC.
Совокупность всех первообразных F(x) + C функцииf(x)называетсянеопределенным интеграломот функцииf(x) и обозначается символом
![]() т.е.
т.е.
![]() (8.1)
(8.1)
В равенстве (8.1) f(x)называется подинтегральной функцией, аf(x)dx–подинтегральным выражением.
Нахождение неопределенного интеграла по данной подинтегральной функции есть действие интегрирования. Геометрически неопределенный интеграл представляет собой множество плоских кривыхy = F(x) + C,которые называютинтегральными кривыми.
Свойства неопределенного интеграла:
Таблица основных неопределенных интегралов:
8.2. Непосредственное интегрирование
Интегрирование, основанное на применении основных свойств неопределенного интеграла и таблицы основных интегралов, принято называть непосредственным интегрированием.
Найти интегралы:
а)
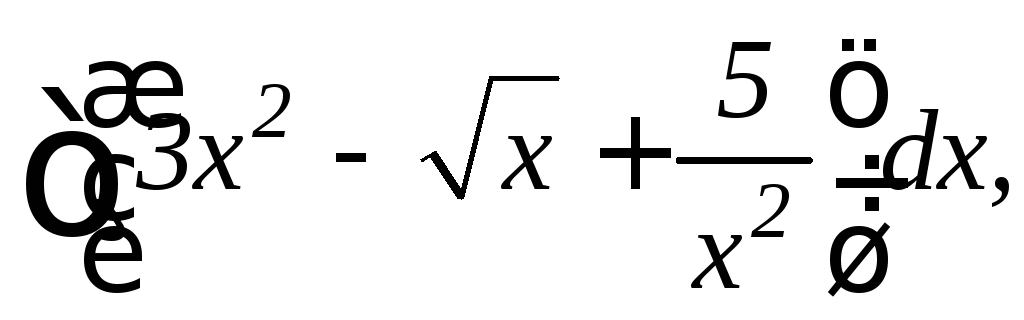
б)
![]()
в)
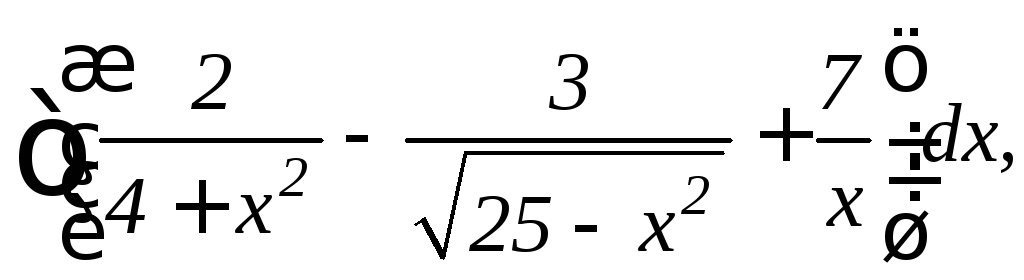
г)
![]()
Решение.
а)
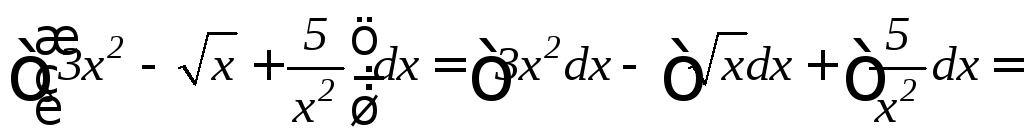
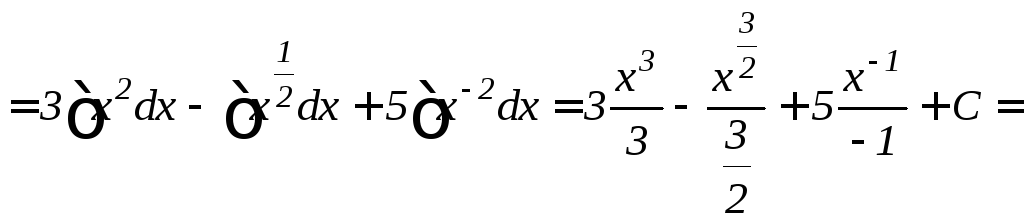
![]()
б)![]()
![]()
в)
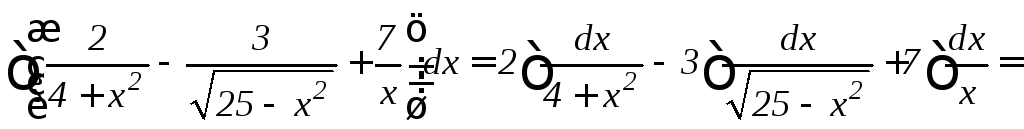
![]()
![]()
г)
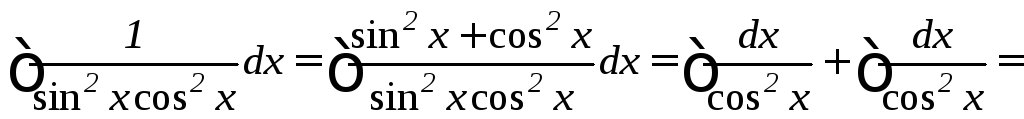
![]()
Задание 8.1. Найти интегралы:
1.
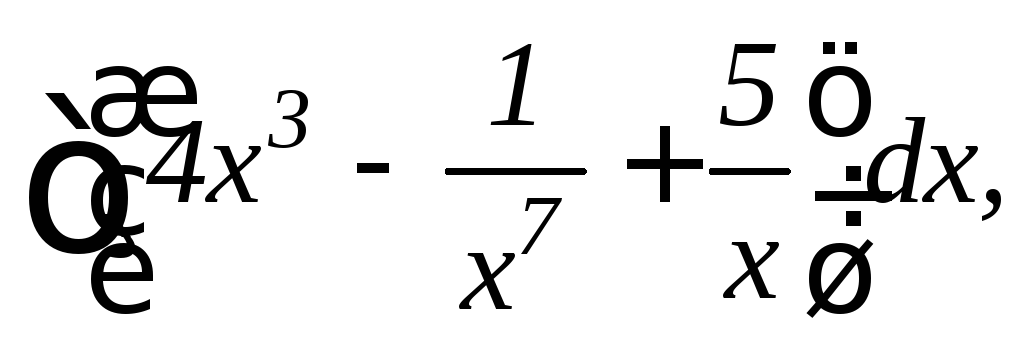 2.
2.![]()
3.
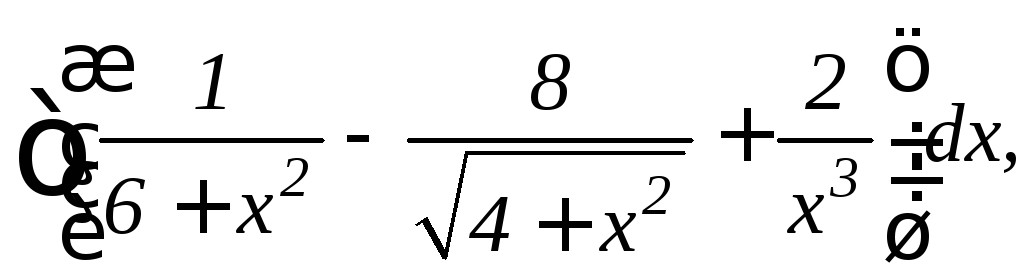 4.
4.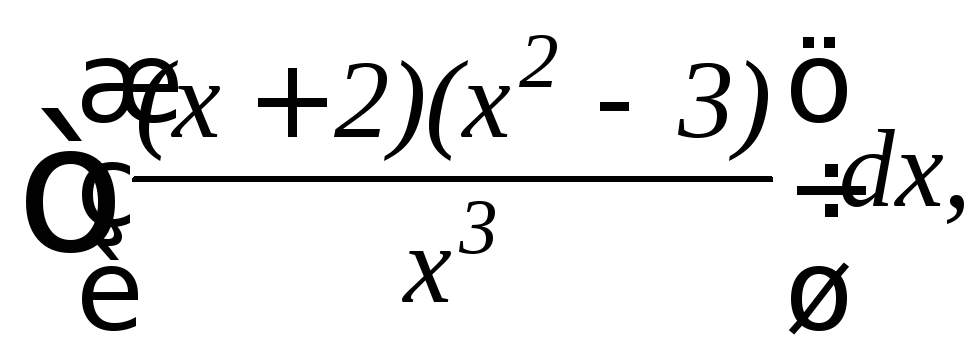
5.
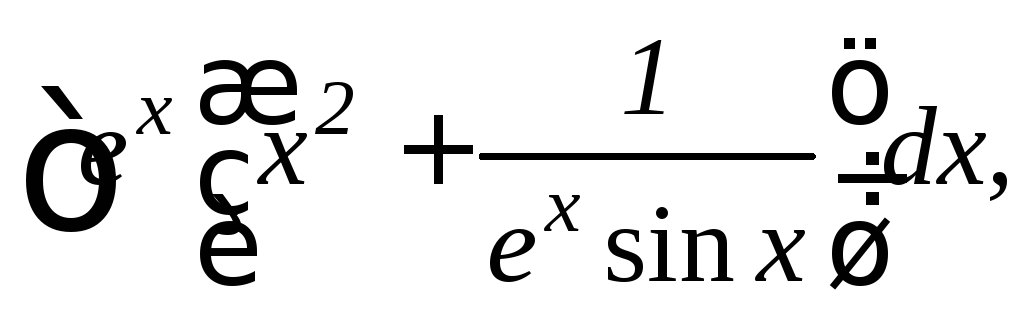 6.
6.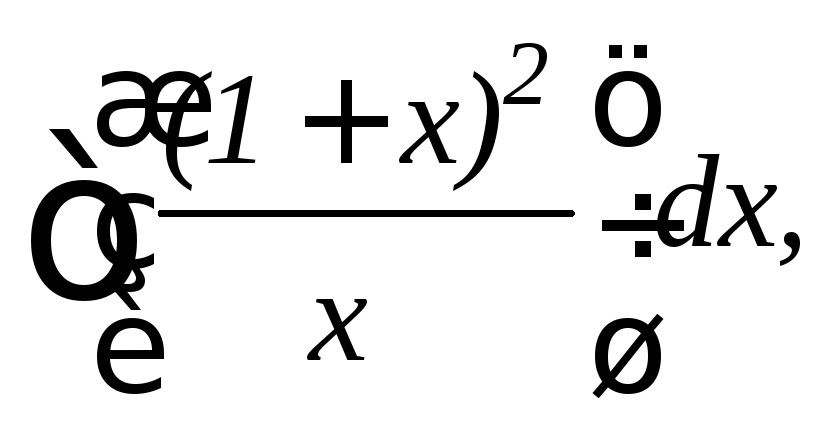
7.
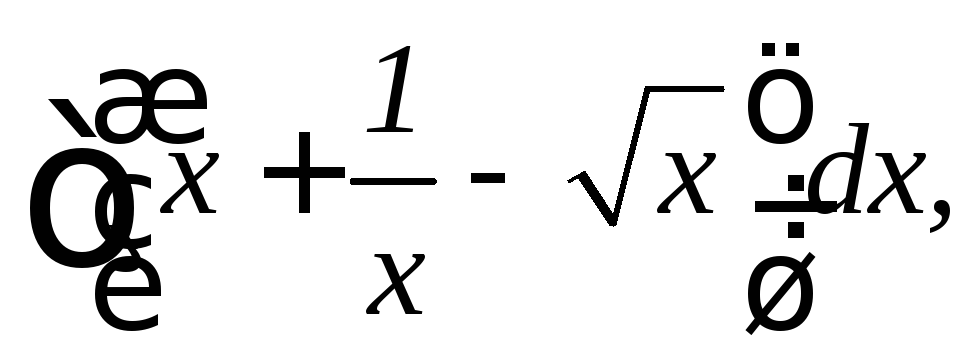 8.
8.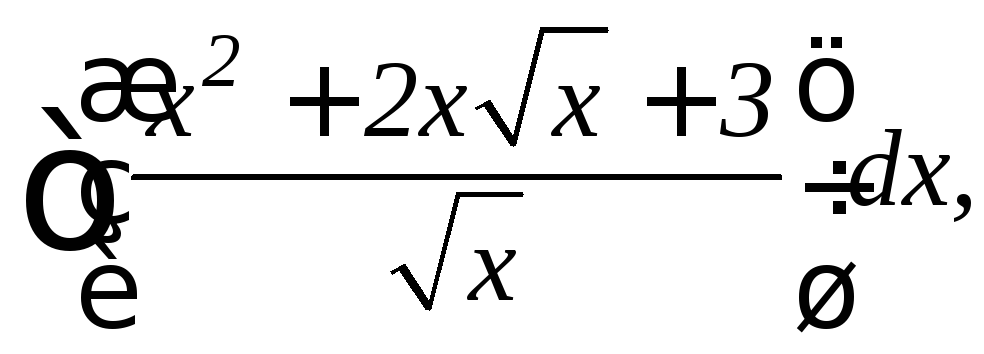
9.
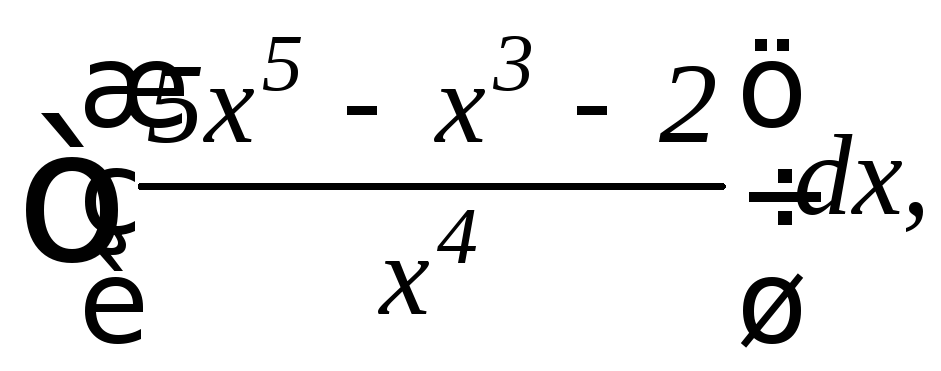 10.
10.![]()
11.
 12.
12.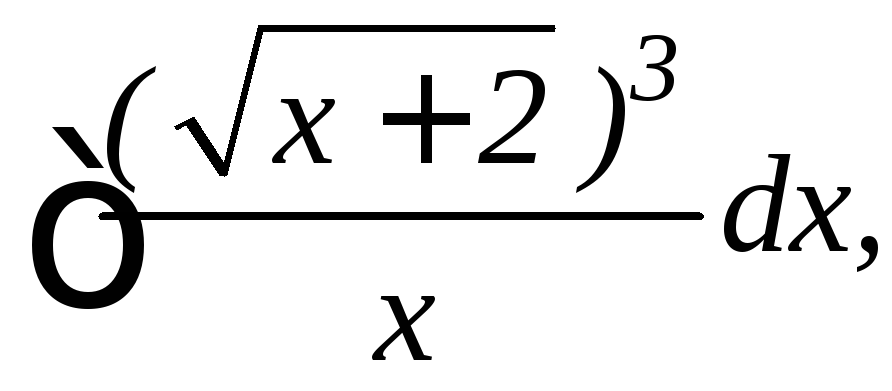
13.
![]() 14.
14.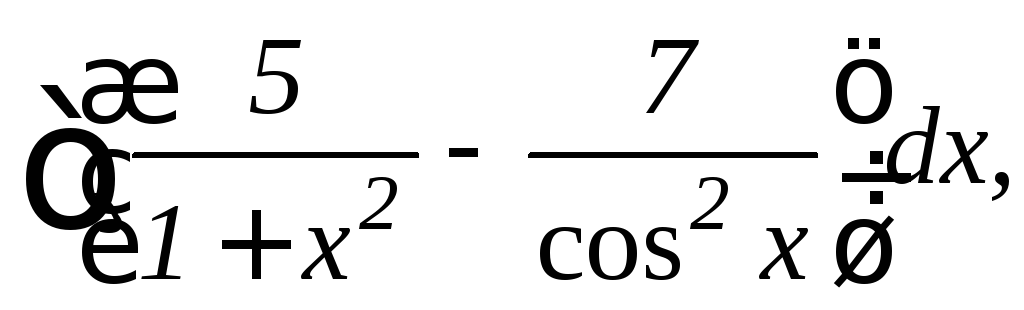
15.
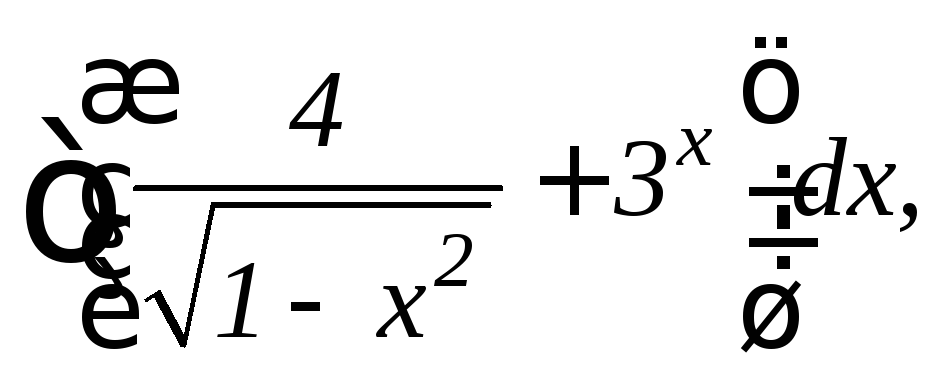 16.
16.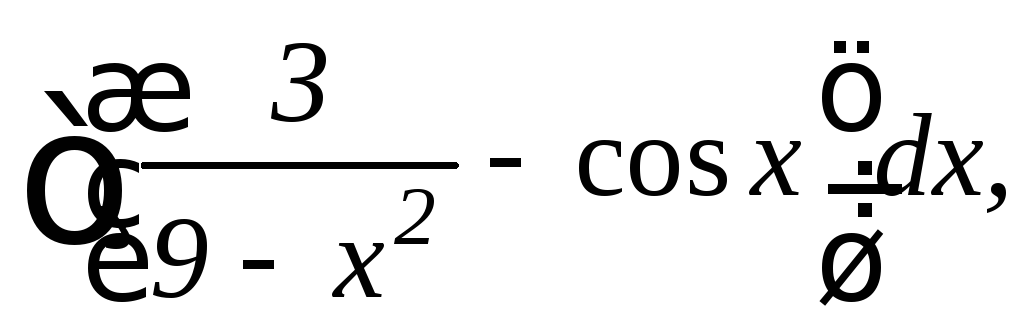
17.
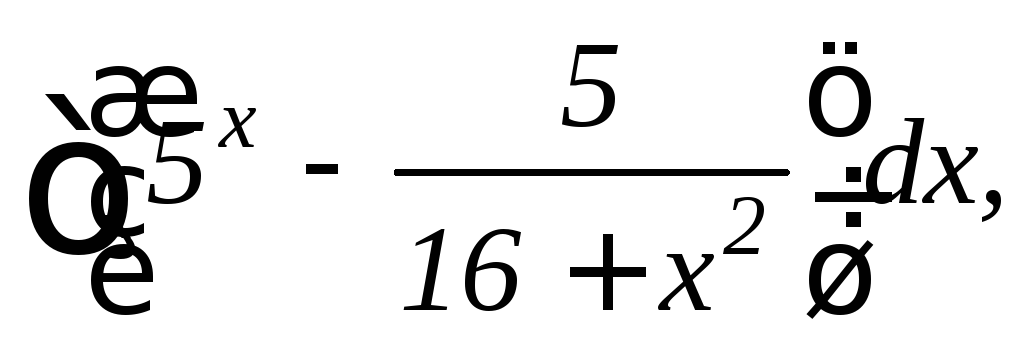 18.
18.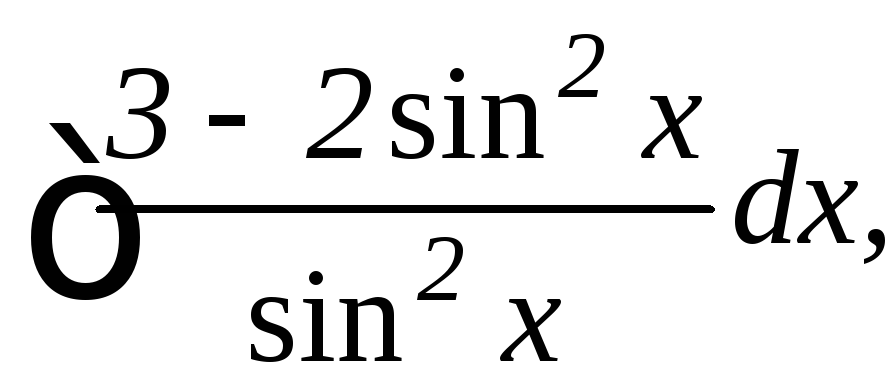
19.
![]() 20.
20.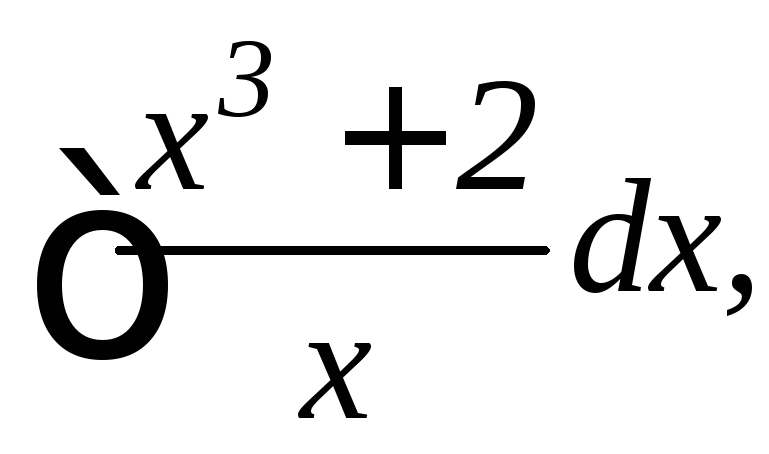
21.
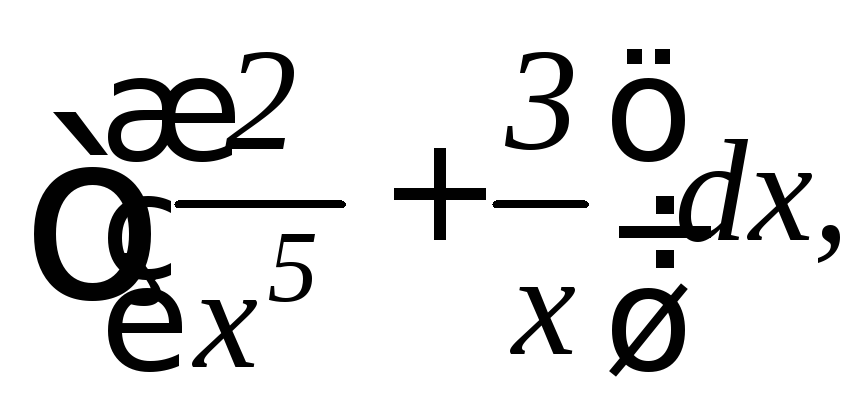 22.
22.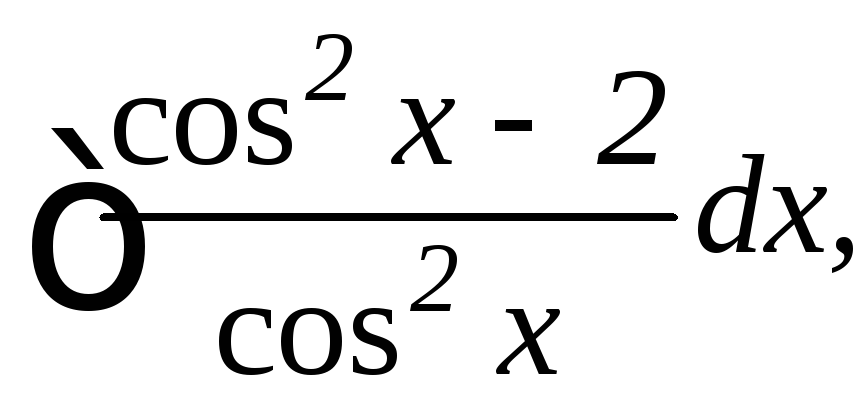
23.
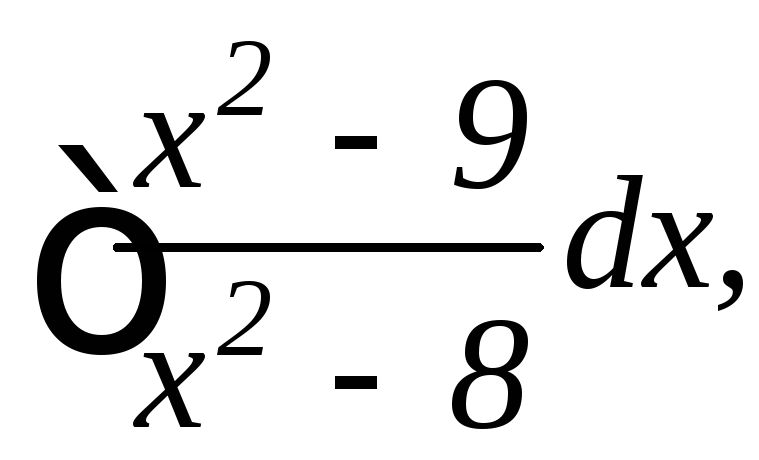 24.
24.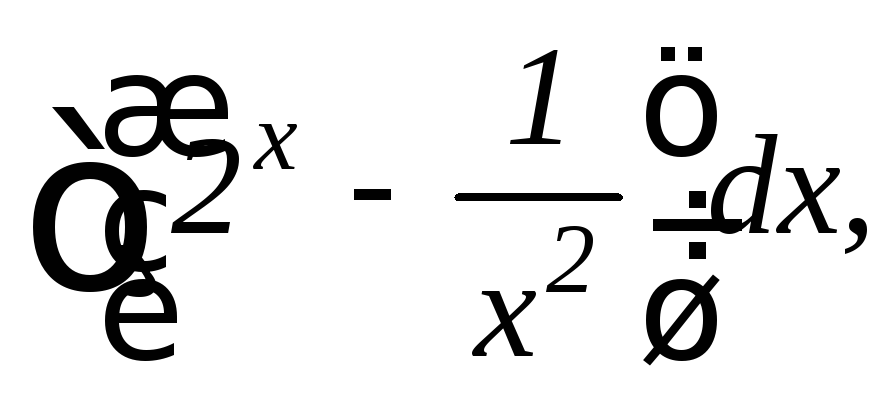
25.
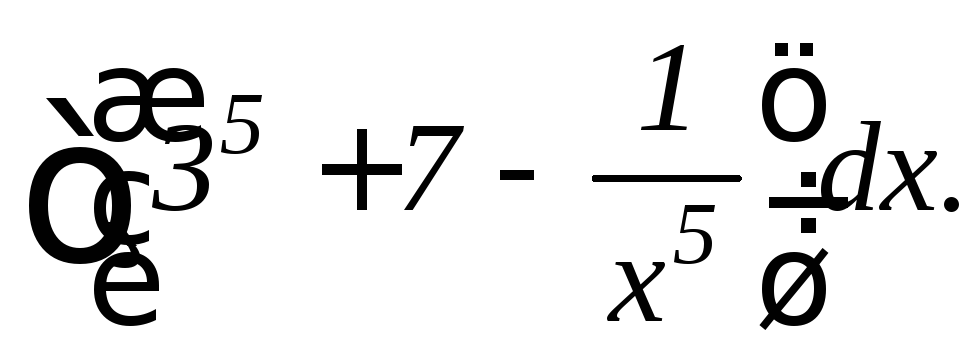
8.3. Метод подстановки
Если интеграл
![]() не является табличным, то часто его
можно упростить путем введения новой
переменнойt. Положимx = φ(t)
– это монотонная и непрерывно
дифференцируемая функция на некотором
промежутке. Если на указанном промежутке
функцияf(x)
интегрируема, то справедливо:
не является табличным, то часто его
можно упростить путем введения новой
переменнойt. Положимx = φ(t)
– это монотонная и непрерывно
дифференцируемая функция на некотором
промежутке. Если на указанном промежутке
функцияf(x)
интегрируема, то справедливо:
![]()
После того, как интеграл найден с помощью подстановки, следует возвратиться к первоначальной переменной x.Иногда вместо подстановкиx = φ(t)применяют подстановкуt = φ(x).
Найти интегралы:
а)
![]()
б)
![]()
в)
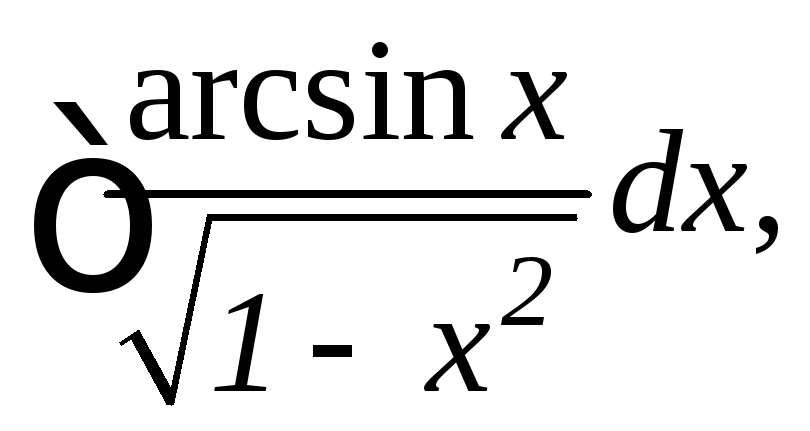
г)
![]()
Решение.
а) Подстановка t
= 7x + 1, тогдаdt = 7dxи dx =
![]()
![]()
б) Подстановка t
= x2 +1,
тогдаdt = 2xdx,
xdx =
![]() .
.
![]()
в) Положим t =arcsinx,
тогда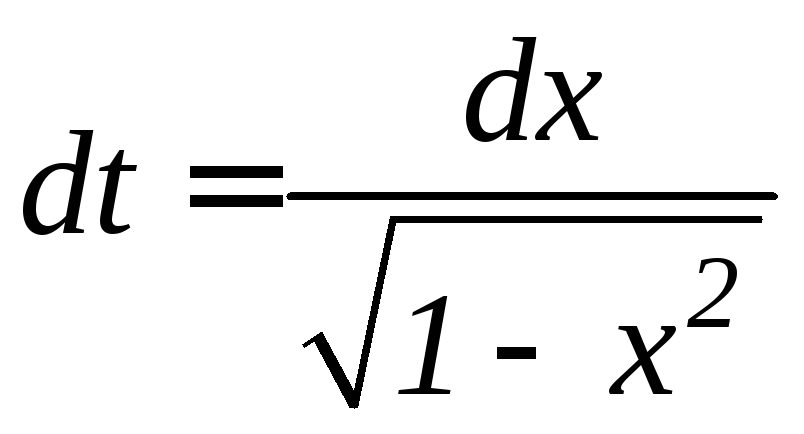 .
.
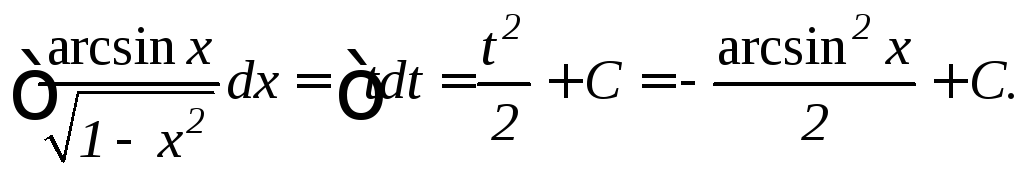
г) Подстановка t =sinx, тогдаdt =cosxdxи
![]()
При решении примеров такого типа можно было бы явным образом не вводить переменную t,а поступать следующим образом:
![]()
Задание 8.2.Методом подстановки найти интегралы.
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
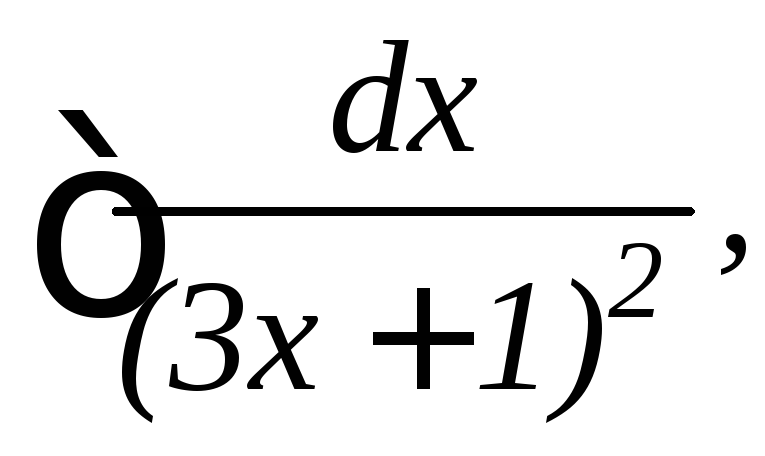 6.
6.![]()
7.
![]() 8.
8.![]()
9.
![]() 10.
10.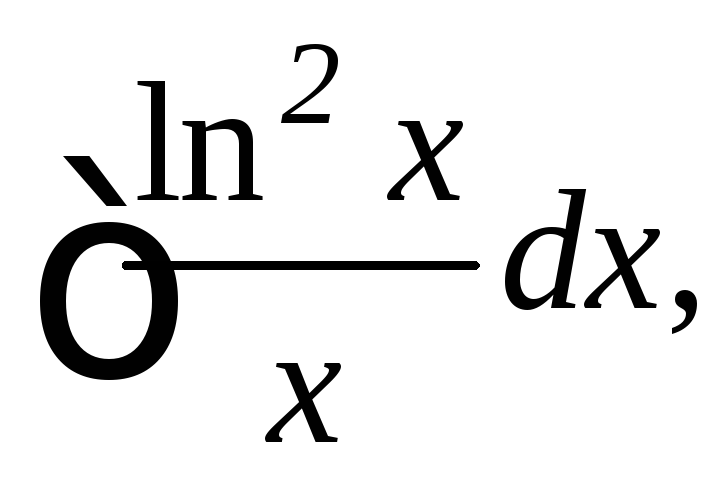
11.
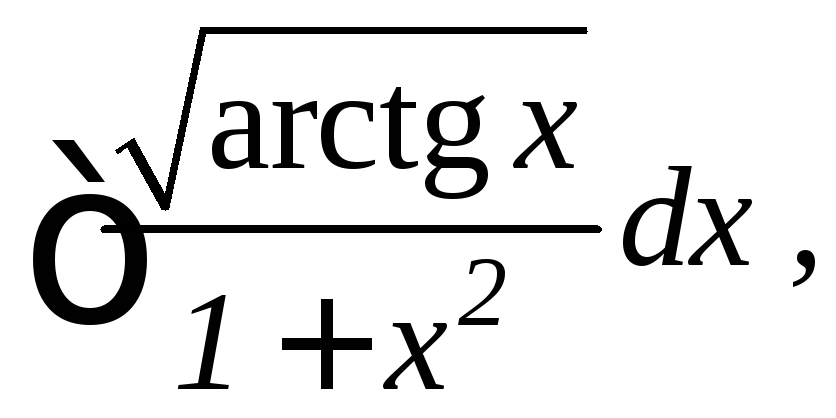 12.
12.![]()
13.
![]() 14.
14.![]()
15.
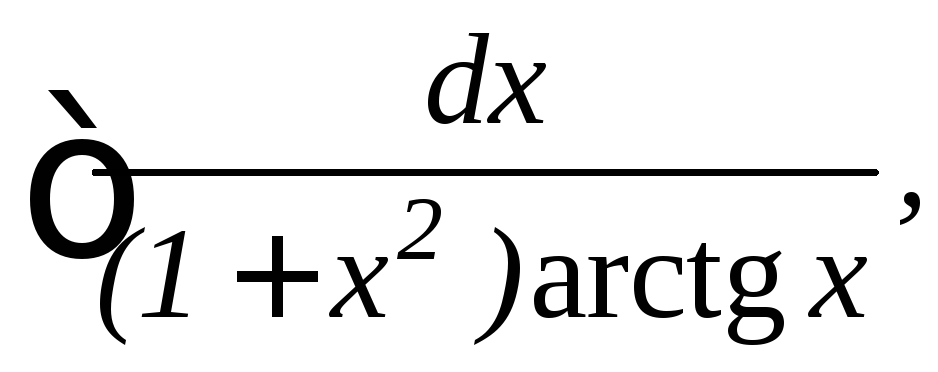 16.
16.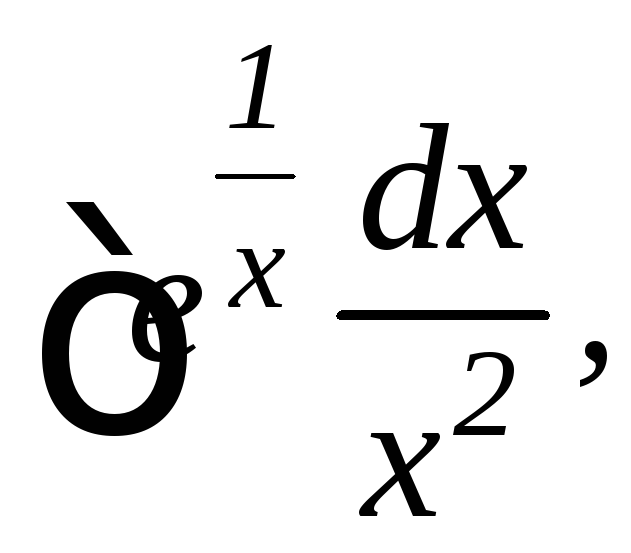
17.
 18.
18.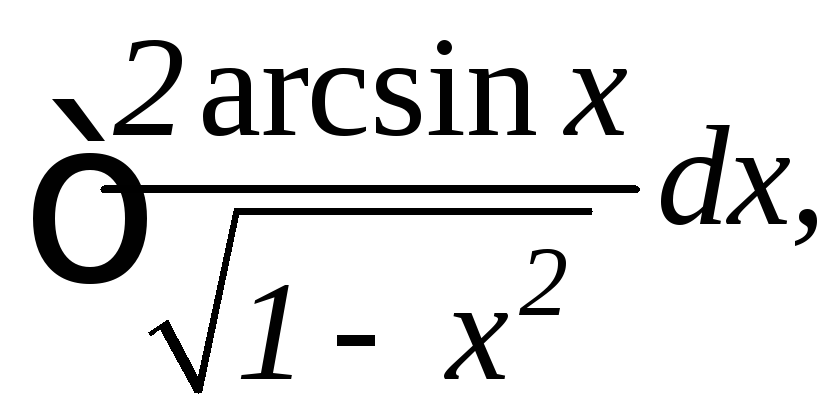
19.
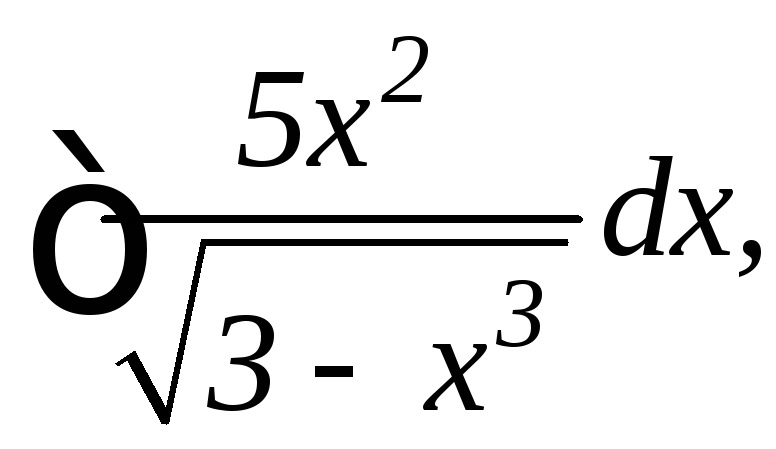 20.
20.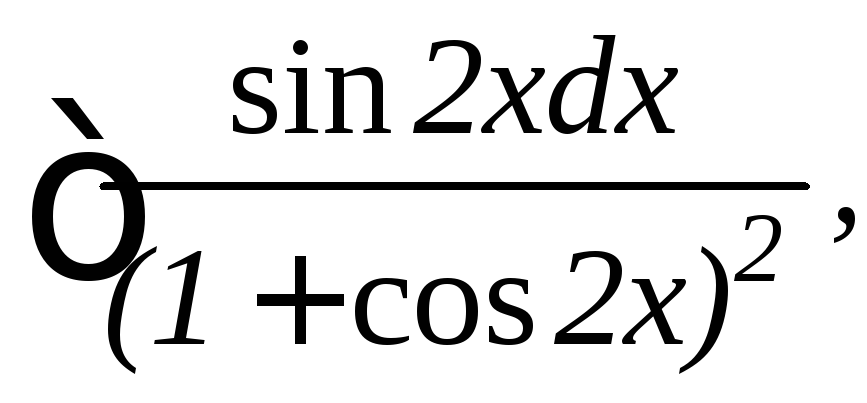
21.
![]() 22.
22.![]()
23.
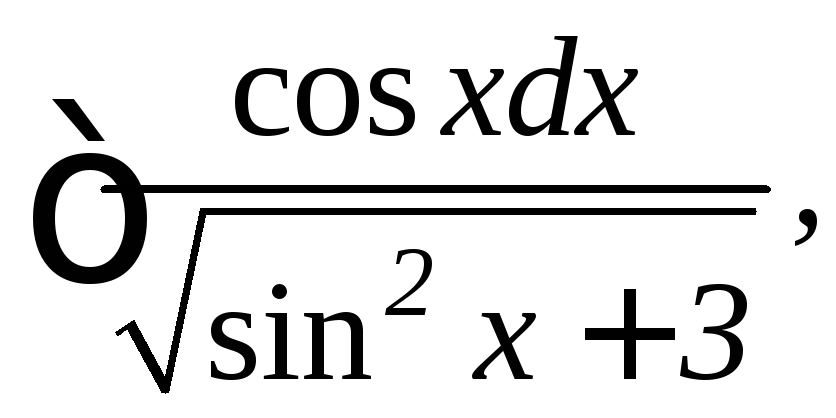 24.
24.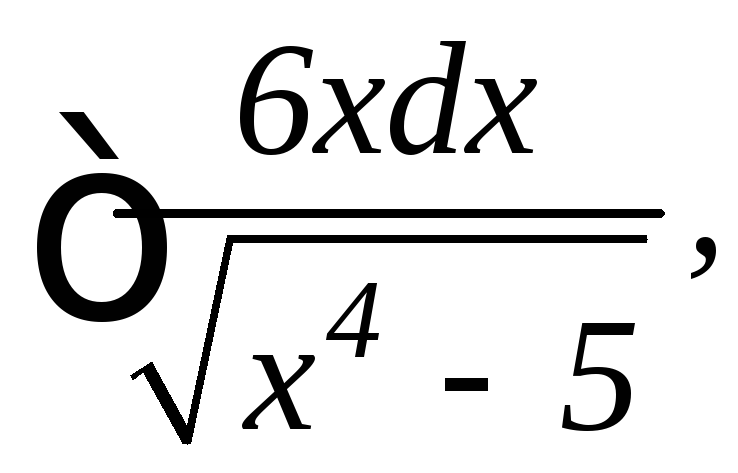
25.
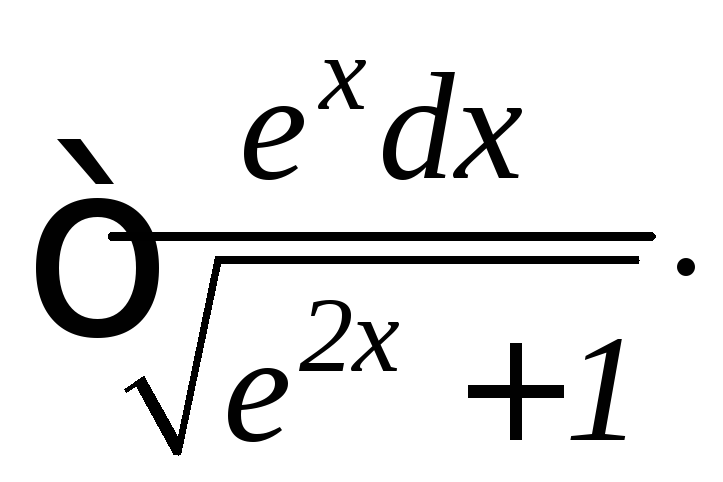
8.4. Интегрирование по частям
Если u(x)
иv(x)
– дифференцируемые функции, то
справедлива формула![]()
Данную формулу интегрирования по частям
применяют в том случае, когда интеграл
![]() более простой в вычислении по сравнению
с
более простой в вычислении по сравнению
с![]()
При этом следует иметь в виду, что если под знаком интеграла стоит произведение многочлена на тригонометрическую или показательную функции, то к u следует отнести многочлен, а оставшееся выражение кdv. Если же подинтегральная функция содержит сомножителем логарифмическую или обратную тригонометрическую функции, то их следует принимать заu, а остальное заdv.
Пример 1.Найти интегралы:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
Решение.
а)
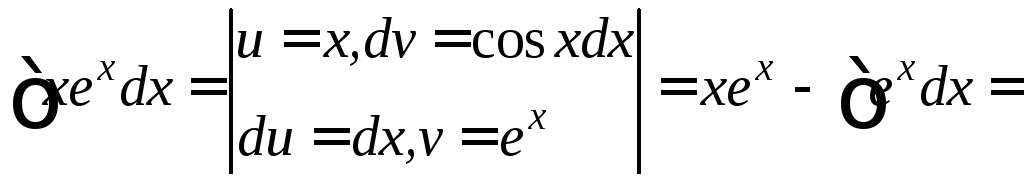
![]()
б)
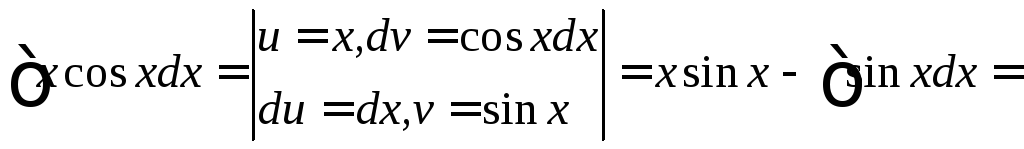
![]()
в)
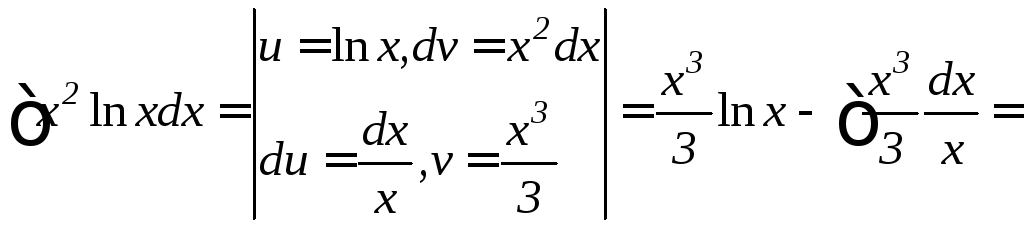
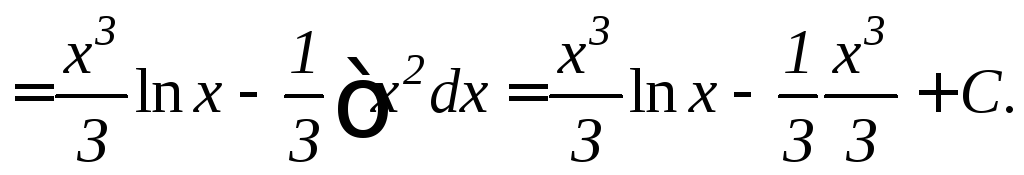
г)
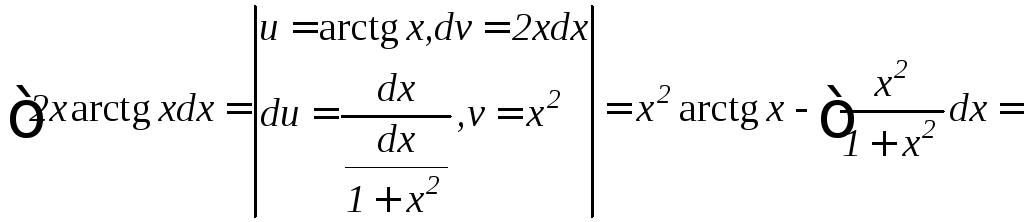
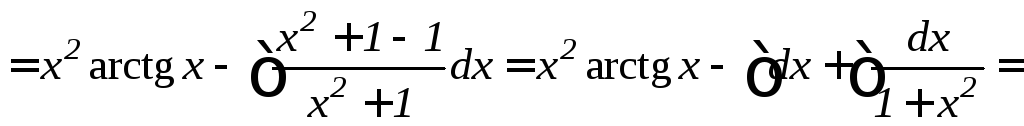
![]()
Задание 8.3. Пользуясь формулой интегрирования по частям, найти интегралы:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.![]()
7.
![]() 8.
8.![]()
9.
![]() 10.
10.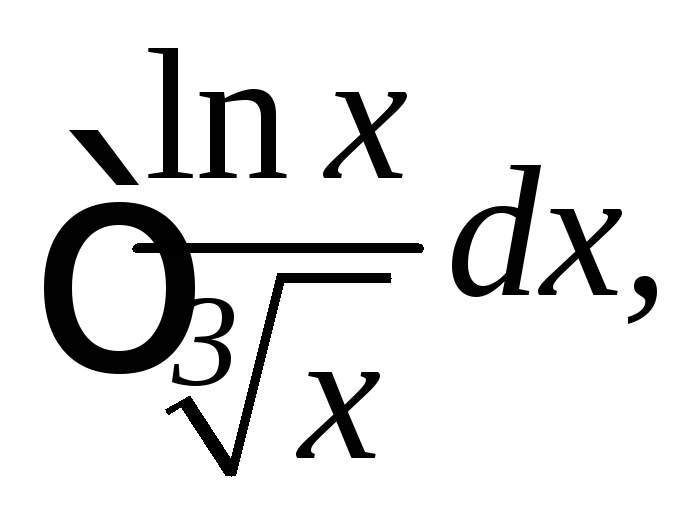
11.
![]() 12.
12.![]()
13.
![]() 14.
14.![]()
15.
![]() 16.
16.![]()
17.
![]() 18.
18.![]()
19.
![]() 20.
20.![]()
21.
![]() 22.
22.![]()
23.
![]() 24.
24.![]()
25.
![]()
Указание.Интегралы вида
![]()
где P(x) – многочлен, следует находить, применяя последовательно формулу интегрирования по частям столько раз, какова степень многочлена.
Иногда после двукратного применения формулы интегрирования по частям, получаем в правой части выражение, содержащее исходный интеграл, таким образом, получаем уравнение с искомым интегралом в качестве неизвестного.
К таким интегралам относятся:
![]()
![]()
![]()
![]()
![]()
![]()
и другие.
а) Найти интеграл
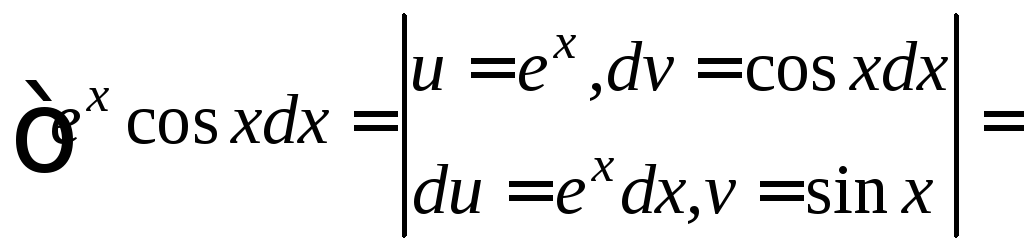
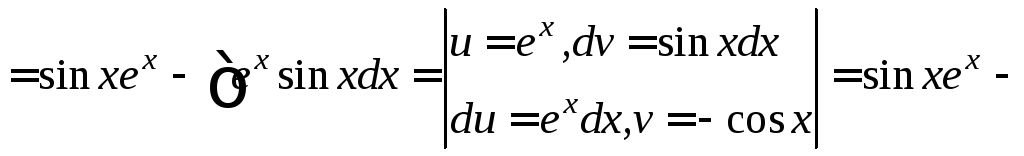
![]()
Т. е. получили уравнение относительно искомого интеграла
![]()
Откуда
![]()
Задание 8.4.Найти интегралы:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.![]()
7.
![]() 8.
8.![]()
9.
![]() 10.
10.![]()