ЛАБ MAPLE ИС / ЛАБ 1-1 матрицы и определители

ЛАБОРАТОРНАЯ РАБОТА № 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

Часть 1. Задание матриц, вычисление их ранга.

Графическое представление матрицы. Вычисление определителей.

Вызываем пакет "Линейная алгебра":

> with(linalg);

Задаём нулевые (пустые) матрицы, определяем их тип, размерность и ранг. Знак % означает результат последней операции, %% - соответственно предпоследней.

> Matrix(2);whattype(%);rank(%%);

> C:=Matrix(3,5);rank(C);

Число строк (rows). Dim – это dimension – размерность (в данном случае размер строки)

> rowdim(C);

Число столбцов (columns)

> coldim(C);

Другие способы задания матриц:

> Matrix(1..2,1..3,8);rank(%);

> A:=Matrix([[1,2,3,4],[1,4,7,9]]);rank(%);

_{Дадим графическое представление элементов матрицы. Для этого вызовем пакет для построения графиков plots (plot – график):}

> with(plots): matrixplot(A,heights=histogram,axes=boxed,orientation=[-60,60]);

ЗАДАНИЯ. 1. Поясните рисунок.

2. Составьте матрицу 3х4 с двумя нулевыми и тремя отрицательными элементами и постройте её график. Поясните полученный рисунок.

> A:=Matrix(3,(i,j)->(i*j));rank(A);

_{Как составлена эта матрица?}

Вычислим миноры определителя этой матрицы:

Вычёркиваем из последней матрицы второй столбец (delcols означает delete columns – удалить столбцы) и строим полученную матрицу:

> delcols(A,2..2);rank(%);with(plots):

matrixplot(A,heights=histogram,axes=boxed,orientation=[-60,60]);

Вычёркиваем вторую и третью строки:

> B:=delrows(A,2..3);rank(%);

matrixplot(B,heights=histogram,axes=boxed,orientation=[-60,60]);

Задаём пустой вектор. По умолчанию это – вектор-столбец (column):

> Vector(2);

Определяем его размерность:

> vectdim(%);

Задаём вектор-строку из девяток и меняем ориентацию вектора. Теперь это вектор-строка (row):

> Vector(1..7,9,orientation=row);

> vectdim(%);

_{Объясните следующие действия:}

> Vector(2,i->x*i);whattype(%);

> Vector(3,i->a^i*(b+i));

> Vector(3,i->a^(i*i)*(b-i),orientation=row);whattype(%);

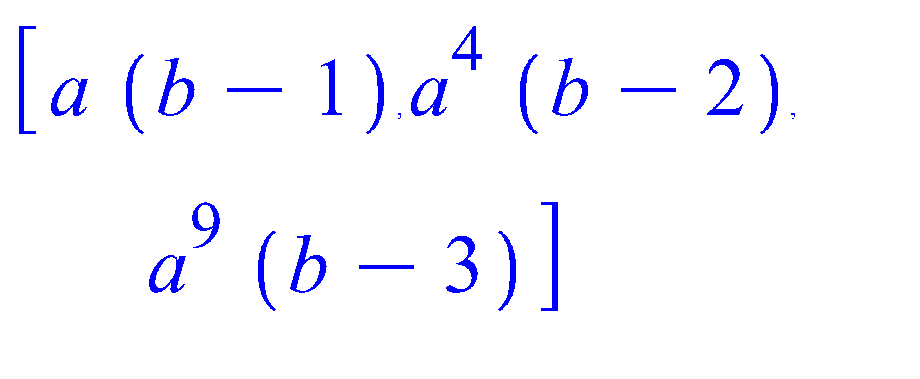
> v1:=<5,7,9>;whattype(%);

> v2:=<1|3|5>;whattype(%);

Создание матрицы по строкам:

> m1:=<<5|8>,<90|89>>;whattype(%);

Создание матрицы по столбцам:

> m2:=<<9,6>|<08,4>>;whattype(%);

Вызываем другой пакет – LinearAlgebra. Обратите внимание, что все команды в этом пакете начинаются с заглавной буквы!

> with(LinearAlgebra):

_{Задаём единичную матрицу:}

> IM:=IdentityMatrix(3,3);Rank(IM);

>

> I1:=IdentityMatrix(3,9);

> matrixplot();

Нулевая матрица

> ZeroMatrix(2,5);whattype(%);

Постоянная матрица. Здесь обратите внимание на различное задание квадратной и прямоугольной матриц.

> ConstantMatrix(100,3);ConstantMatrix(52,3,2);

Матрица с переменными.

> ScalarMatrix(a^5,2);

Единичный вектор с единицей на заданном месте. Здесь вектор – это матрица-столбец.

> UnitVector(3,6);

Зададим вектор-строку с помощью опции [row]:

> UnitVector[row](8,10); #Длина не больше 10

Нулевой и постоянный векторы

> ZeroVector[row](9);

> ConstantVector[row](307,4);

Зададим переменные х и у и присвоим им какие-либо числовые значения.

> x:=5;y:=10;

> ScalarVector[row](x+y,3,7);

Что означают цифры 3, 7 и 15?

Матрицы слишком большой размерности (>10) вычисляются, но не отображаются:

> Matrix(16,16,(i,j)->i+j);

> Matrix(10,10,(i,j)->i+j);

Эта матрица отобразилась, т.к.её порядок не больше 10.

Часть 2. Действия с матрицами.

Вычисление определителей квадратных матриц

> restart:

> with(linalg):

Задаём квадратную матрицу

> A:=<<5,1,-1>|<-3,1,-2>|<1,1,2>>;

Вычисляем её определитель:

> det(A);

Вычислим её минор, остающийся после вычёркивания 1-й строки и 2-го столбца:

>

Вычислим другие миноры:

>

>

Зададим другие матрицы.

>

>

>

>

>

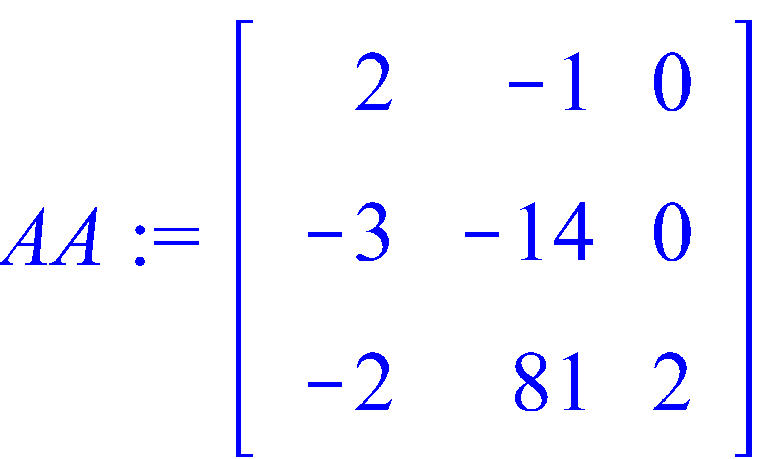
В пакете linalg так складывать матрицы нельзя. Вызовем другой пакет.

>

>

>

>

>

Здесь действие сложения было произведено.

Сложение матрицы со скаляром равносильно сложению матрицы с диагональной матрицей, т.е. с единичной матрицей, элементы которой умножены на этот скаляр:

>

Умножим матрицу на скаляр (число).

>

>

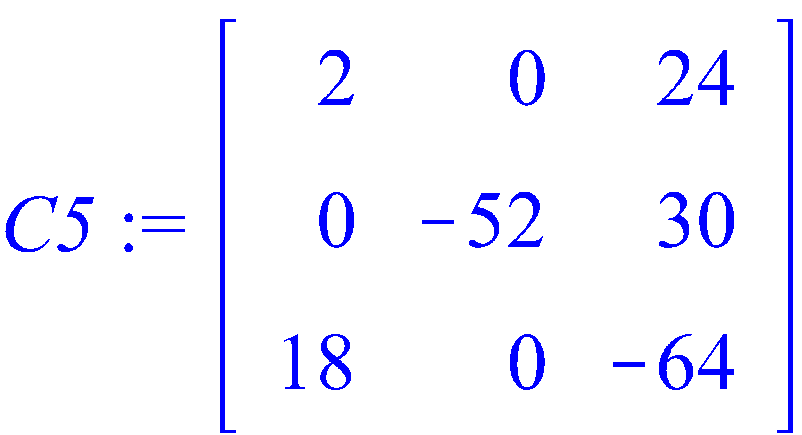
Умножим матрицу на дробное число.

>

Видим, что умножение матриц на дробные числа производится неправильно, т.е. в 17-м и 18-м знаках появляются какие-то цифры.

Зададим матрицу не из целых, а из вещественных чисел:

>

>

Результат тот же. Перемножим числа.

>

Числа перемножаются правильно.

Зададим квадратную матрицу.

>

_{Прибавим к каждому элементу матрицы единицу:}

>

Теперь определитель отличен от нуля.

Задания

1. Составить квадратные матрицы 1-го, 2-го, 3-го, 4-го и 5-го порядков и вычислить их определители в двух пакетах линейной алгебры. Вычислить несколько миноров. Построить графики трёх любых матриц.

2. Задать матрицу с двумя пропорциональными строками, вычислить определитель. Изменить один элемент матрицы так, чтобы определитель стал ненулевым.

3. Проиллюстрировать другие свойства определителей. Для иллюстрации теорем разложения и аннулирования использовать команду minor.