ЛАБ MAPLE ИС / лаб 09-1-ряды-суммы-задание

ЛАБОРАТОРНАЯ РАБОТА № 7-1. РЯДЫ

ЧАСТЬ 1. ВЫЧИСЛЕНИЕ СУММ

1. Вычислим сумму ряда с общим членом , используя неактивную форму Sum():

> Sum(1/k^2,k=1..infinity)=sum(1/k^2,k=1..infinity);

Найдём приближённое значение:

> evalf(%);

Вычислите частичную сумму этого ряда, взяв 100 членов:

> Sum(1/k^2,k=1..100)=sum(1/k^2,k=1..100);

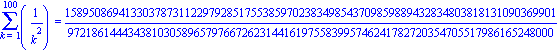
Разложим на множители знаменатель дроби denom. Для разложения его на простые множители используем команду ifactor:

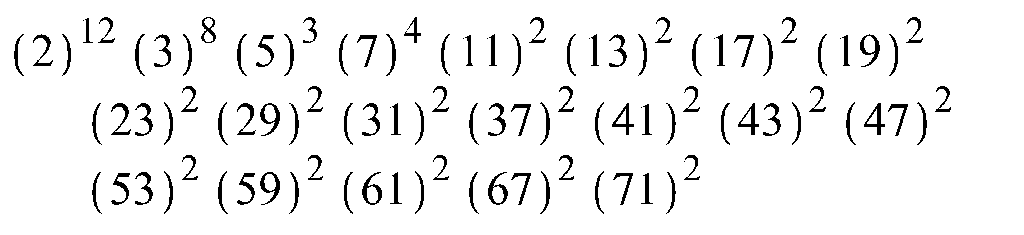
Проверим, является ли числитель этой дроби простым числом. Используем команду вычисления числителя дроби numer (вычисление может занять до 10 минут).

Теперь вычислим приближённое значение дроби s100:

> evalf(s100);

Задание. Придумать дробь с 30-ю цифрами в числителе и знаменателе. Разложить их на простые множители. Сократить дробь, если это возможно.

2. Просуммируем 3 первых члена гармонического ряда с чётными номерами. Индексы 2, 4, 6 зададим как корни уравнения (x-2)(x-4)(x-6)=0.

> sum(1/k,k=RootOf((x-2)*(x-4)*(x-6)));

Какие числа складываются для получения 11/12?

Вычислите сумму первых 3 нечётных членов ряда .

> sum(1/k^3,k=RootOf((x-1)*(x-3)*(x-5)));

Какие числа складываются для получения этого результата?

3. Суммы можно вычислять и с помощью процедуры add(выражение, диапазон). Найдём сумму квадратных корней первых четырёх натуральных чисел:

> add(sqrt(n),n=1..4);

> evalf(%);

Теперь с помощью процедуры seq() создадим последовательность этих квадратных корней.

> s:=seq(sqrt(n),n=1..4);

> add(n,n=s);

Различие между процедурами sum() и add() заключается в том, что sum() пытается вычислить сумму в символьной форме. Процедура add() – в числовой. Найдём сумму ряда с общим членом :

> Sum((2*n-1)/(2^n),n=1..infinity)=sum((2*n-1)/(2^n),n=1..infinity);

Добавим параметр b:

> Sum((2*n*b-1)/(2^n),n=1..infinity)=sum((2*n*b-1)/(2^n),n=1..infinity);

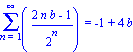
При каком значении b получается предыдущая сумма? Напишите равенство при b=10.

4. Вычисление числа пи.

Математикам хорошо известна формула вычисления числа π, полученная индийским математиком Рамануджаном в 1910 году путём разложения арктангенса в ряд Тейлора:

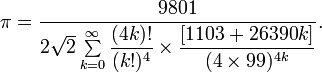(1)

Уже при k = 100 достигается огромная точность — шестьсот верных значащих цифр!

4.1. Проверка формулы Рамануджана для точного вычисления числа 1/пи

>

>

> _;

Вычислим число пи как обратное к ipi:

>

Теперь запишем первые 600 знаков встроенного в Maple числа Pi:

>

Вычислим погрешность:

>

Видим, что числа совпадают с точностью до 600 знаков.

4.2. Вычисление числа пи с помощью суммы знакочередующегося ряда

.

Зададим сумму 100 членов ряда:

> _;

Сравним с «точным» значением:

Какой ряд лучше приближает число пи?

Задания.

1. Вычислить число пи по формуле Рамануджана (1) при k=20, сравнить с числом Pi из Maple.

2. Проделать то же при k=10. Вычислить погрешность.

5. Другие формулы Рамануджана

5.1.

(2)

Задания.

1. Вычислить суммы 6 и 7 членов ряда (2). Сравнить с правой частью. Обратить внимание на знак погрешности.

2. Составить процедуру для вычисления суммы произвольного числа п членов ряда (2). Общий член ряда имеет вид

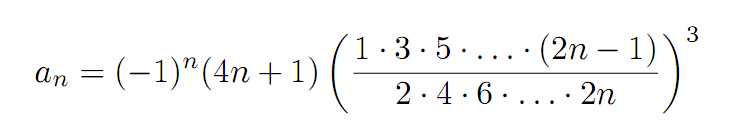
Проверить работу процедуры для п =11 и п = 50. Вычислить погрешность.

5.2.

(3)

Задания.

1. Вычислить левую часть формулы (3). Сравнить с правой частью.

2. Продолжить левую часть формулы (3) ещё на 2, затем на 6 радикалов. Сравнить с правой частью.

3. Составить процедуру для вычисления произвольного числа п радикалов (3). Проверить для п =10 и п = 50. Вычислить погрешность.

5