ЛАБ_ РАБ_ОТУ_ИС3_мод

ЛАБОРАТОРНЫЕ РАБОТЫ

по курсу

"Технологии искусственного интеллекта в управлении"

Работу выполнять спокойно и вдумчиво!

Справочный материал по комплексным числам и матрицам приведен в приложении.

Все работы выполняются с письменным отчетом с фиксацией графиков экранных форм).

Оформление результатов работ. Отчет работы должен иметь следующие составляющие.

1. Титульный лист.

2. Введение (цель работы, основные положения).

3. Задание (задача).

4. Способ решения поставленной задачи (математические формулы).

5. Схема компьютерной модели.

6. Результаты решения (числовые результаты, экранные формы, графики).

7. Выводы по работе.

Работа N 1

Имеется дифференциальное уравнение. Вывести операторное описание, передаточную функцию и частотные характеристики, описание в пространстве состояний

а)

y⁽³⁾ + 2 y⁽²⁾ + 5y⁽¹⁾ + 8y(t) = u(t):

б)

y⁽²⁾ + 3y⁽¹⁾ + 2y(t) = u(t);

в)

y⁽²⁾ + 5y⁽¹⁾ + 6y(t) = u(t).

Частотные характеристики непрерывных систем

Основные положения

Графическое построение характеристик непрерывных систем в рамках программного продукта MatLab проводится следующим образом.

1. Запустить MatLab. В правом окне появится знак > командной строки.

2. Набрать в командной строке h = tf([3], [2,1]), что соответствует передаточной функции (transfer function)

5

W(s) = --------------------

2s + 1

и нажать кнопку ВВОД. На экране монитора отразится эта передаточная функция.

3. Если в командной строке набрать nyquist(h) и нажать кнопку ВВОД, то в раскрывающемся окне отразится амплитудно-фазовая частотная характеристика W(j). Она отражается для частот от -  до + . Чтобы убрать отражение для отрицательных частот, необходимо нажать правую кнопку и в раскрывшемся окне выбрать пункт show и снять "галочку" в раскрывающейся позиции "negative frequencies". "Кликнув" на полученной характеристике, возможно поставить красную точку, рядом с которой раскрывается окно с указание числовых значений вещественной и мнимой частотных характеристик и текущей частоты. Точку можно "протягивать" мышью вдоль характеристики.

4. Если в командной строке набрать bode(h), и нажать кнопку ВВОД, то в раскрывающемся окне появятся амплитудная и фазовая частотные характеристики.

5. Если в командной строке набрать step(h), и нажать кнопку ВВОД, то в раскрывающемся окне появится переходная функция h(t). При наборе в командной строке impulse(h) в раскрывающемся окне появится импульсная переходная функция w(t).

Замечание. После набора h каждую функцию можно выбрать только один раз. Для повторного вызова надо снова набрать h.

ЗАДАНИЕ

Типовые звенья.

Свериться с характеристиками в справочнике. При отсутствии справочника составить таковой, зарисовав и проанализировав соответствующие характеристики.

А. Определить и ввести в персональный справочник ВСЕ перечисленные ВЫШЕ характеристики для следующих случаев.

1. Безинерционное звено

W(s) = 5.

2. Интегрирующее звено

W(s) = 5/s.

3. Дифференцирующее звено

W(s) = 5s.

Переходную и импульсную переходную функции не определять.

4. Инерционное звено первого порядка

4

W(s) = -------------------- .

3s + 1

5. Инерционное звено второго порядка

3

W(s) = -------------------- .

4s² + 3s + 1

Зарисовать графики и проанализировать их правильность.

Б. Построить частотные характеристики

1. ПИ-регулятора

W(s) =2 + 3/s.

2. ПИД-регулятора

W(s) =2 + 4s + 3/s.

В. Имеется система с единичной отрицательной обратной связью. Передаточная функция прямой цепи W(s). Определить устойчивость замкнутой системы по амплитудно-фазовой W(j) и логарифмическим частотным характеристикам L() и () для следующих передаточных W(s).

1.

3

W(s) = -------------------------- .

s(10s + 1)(5s + 1)

2.

3

W(s) = -------------------------- .

s²(10s + 1)

3.

10(3s + 1)

W(s) = -------------------------- .

s(10s + 1)(0.1s + 1)

4.

20(0.1s + 1)

W(s) = ----------------------------- .

s(0.5s + 1)(0.02s + 1)²

5.

10(3s + 1)

W(s) = -------------------------------------- .

s(10s + 1)(0.1s + 1)(0.05s + 1)

Работа N 2

Частотные характеристики соединений непрерывных систем

Основные положения

1. Набрать в командной строке h1 = tf([3], [1,0]) и h2 = tf([3], [1, 2]).

2. Найти характеристики

последовательного соединения

series(h1, h2);

параллельного соединения

parallel(h1, h2);

соединения с обратной связью (компьютер настроен на отрицательную обратную связь)

feedback(h1, h2).

ЗАДАНИЕ

А. 1. Набрать в командной строке h1 = tf([3], [1,1]), h2 = tf([3], [1, 2]).

Определить характеристики последовательного соединения..

Б. 1. Набрать в командной строке h1 = tf([3], [1,0]), h2 = tf([-1]). Ввести feedback(h1, h2). Определить вид изменения характеристики h1.

2. Набрать в командной строке h1 = tf([3], [2, 1]), h2 = tf([-1]). Ввести feedback(h1, h2). Определить вид изменения характеристики h1.

3. Набрать в командной строке h1 = tf([1]), h1 = tf([2, 1], [3]). Ввести feedback(h1, h2). Сравнить передаточную функцию соединения с предыдущим случаем.

Работа N 3

Описание вход-выход и в пространстве состояний.

ЗАДАНИЕ

А. Набрать в пространстве состояний

sys = ss([-2 -1; 1 -2], [1 1; 2 -1 ], [1 0], [0 0]).

Найти передаточную функцию вручную (обратная матрица (sI – А), произведение матриц C(sI – А^)-1B) и с помощью компьютера. Сравнить полученные результаты.

tf(sys).

Б. Набрать передаточную функцию

h =tf([2,1],[1, 3, 5]).

Найти описание в пространстве состояний вручную и с помощью компьютера, набрав ss(h).

В. Набрать матрицы [0 1; -2 -3], [0 2], [1 0], [0]. Найти передаточную функцию вручную (определить обратную матрицу (sI – А)^-1, произведение матриц C(sI – А)^-1B) и с помощью компьютера. Сравнить полученные результаты.

Г. По передаточной функции

2

W(s) = ----------------------- ,

s² + 3s + 1

определить матрицы A, B, C, D. Почему результат не совпадает со значением пункта В?

Работа N 4

Работа с SIMULINK.

1. Запустить MatLab. В правом окне появится знак > командной строки.

2. Набрать в командной строке SIMULINK, ВВОД.

3. Выбрать в меню File позицию File/new/model. Справа появится новое окно-контейнер.

4. Выбрать и перенести в контейнер блоки, расположив их слева направо

из папки Source - блок Step (скачок)

из папки Continous - блок Transfer FCN 3s/[s(s + 1)]

из папки Sinks - блок Scope (осциллограф).

5. Соединить блоки с помощью мыши, "протаскивая" связи от выхода ко входу.

6. Запустить систему для получения переходной функции, нажав кнопку Start/Pause Simulation в панели инструментов SIMULINK.

7. Чтобы увидеть процесс во времени, необходимо дважды кликнуть на блоке Scope.

8. Перенастроить параметры блоков.

9. Если процесс необходимо остановить, надо нажать кнопку Stop в панели инструментов SIMULINK.

ЗАДАНИЕ

А. Имеется система с единичной отрицательной обратной связью. Передаточная функция прямой цепи W(s). Определить поведение замкнутой системы. Для организации обратной связи использовать в контейнере блок (сравнивающее устройство) Sum папки Math Operations. «Кликнув» на блоке, заменить один знак + (плюс) на – (минус).

1.

3

W(s) = -------------------------- .

s(10s + 1)(5s + 1)

2.

3

W(s) = -------------------------- .

s²(10s + 1)

3.

10(3s + 1)

W(s) = -------------------------- .

s(10s + 1)(0.1s + 1)

4.

20(0.1s + 1)

W(s) = ----------------------------- .

s(0.5s + 1)(0.02s + 1)²

Б. Заменить в предыдущем пункте передаточную функцию W(s) на функцию в пространстве состояний A= [-2 -1; 1 -2], B=[1 1; 2 -1 ], C=[1 0], D=[0 0]. Для этого использовать из папки Continous - блок State Space.

В. Набрать передаточную функцию

h =tf([2,1],[1, 3, 5]).

Г. Найти описание в пространстве состояний ss(h). Выполнить предыдущие пункты для заданной передаточной функции и описания в пространстве состояний. Сравнить результаты.

Н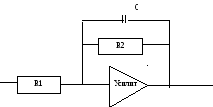айти передаточную функцию для схемы и отобразить ее частотные характеристики L() и ()

Приложение

Комплексные числа.

Комплексное число k = a + ib = me^j, где a и b - вещественная и мнимая части; m - модуль,  - фаза, m = (a² + b²)^1/2,  = arctg (b/a), i = -1.

Сопряженным комплексным числом к числу k является комплексное число k1 = a - ib. Устранение комплексности в знаменателе

1/(a + ib){(a - ib)/(a - ib)} = a/( a² + b²) - ib/(a² + b²).

В курсе основ теории управления (ОТУ) общепризнанно применяются другие обозначения, соответствие которых приведено в таблице.

Математика	ТИИУ
i	j
a	P()
b	Q()
m	R()
	()
-	L() = 20lgR()

Значения некоторых функций

ej^t = cost + sint, c/0 = , где c - любое число, не равное бесконечности, дп1 = 0, дп10 = 1, e⁰ = 1.

x	0	/4	/2		- /4	- /2	- 
sinx	0	(2)1/2/2	1	0	- (2)1/2/2	-1	0
cosx	1	(2)1/2/2	0	- 1	(2)1/2/2	0	-1
tgx	0	1		0	- 1		0

Производные

(t^a)' = at^{a - 1}, e^at = ae^at. Интеграл e^atdt = (1/a)e^at .

Матрицы.

Матрица - таблица вида

	a11	a12	a13
M =	a21	a22	a23
	a31	a32	a33

Определитель d матрицы d = a₁₁ a₂₂ a₃₃ + a₁₃ a₂₁ a₃₁ + a₃₁ a₁₂ a₂₃ - - a₁₃ a₂₂ a₃₁ - a₁₁ a₃₂ a₂₃ - a₃₃ a₂₁ a₁₂.

Имеет место единичная матрица

	1	0	0
E =	0	1	0
	0	0	1

Для матрицы M существуют транспонированная матрица M^T и обратная матрица M ^-1.

Транспонированная матрица

	a11	a21	a31
MT =	a12	a22	a32
	a13	a23	a33

Обратная матрица M ^-1 получается из выражения

M M ^-1 = M ^-1M = E.

	A11	A21	A31
M-1 = (1/d)	A12	A22	A32
	A13	A23	A33

где элементы A_ji характеризуют приведенную матрицу.

Aii получается как определитель матрицы, полученной вычеркиванием i-й строки и i-го столбца.

A_ij получается тем же путем, но со знаком минус и транспонированием элемента.

Умножение матриц.

Пусть матрица M имеет размерность 2  2 и

	b11	b12
N =
	b21	b22

Матрица-произведение

	a11	a12		b11	b12		c11	c12		a11 b11 + a12 b21	a11 b12 + a12 b22
P = MN =						=			=
	a21	a22		b21	b22		c21	c22		a21 b11 + a22 b21	a21 b12 + a22 b22

Иными словами в общем виде

_n

c_ik =  a_ij b_jk , i = 1, n; j = 1, n; k = 1, n.

^{j =1}

(AB)^T = B^TA^T, (AB) ^-1 = B^-1A^-1.

Прямое преобразование Лапласа

_

Y(s) = y(t)e^-stdt

⁰

Наиболее распространенными типовыми воздействиями среды на систему являются единичная импульсная -функция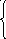

, при t = 0, _

(t) = (t)dt = 1,

0, при t  0, ^{- }

единичная функция

0, t < 0,

1(t) =

1, t  0.

Функция

Y(s) = B(s)/A(s)

является дробно-рациональной и при простых полюсах

y(t) = B_Y(s_j)/A'_Y(s_j)exp(s_jt),

где A'_Y(s) производная по s.

Преобразование Лапласа

y(t)	Y(s)
1(t)	1/s
(t)	1
t	1/s2
ejt	(s + j)/(s2 + 2)
cost	s/(s2 + 2)
sint	/(s2 + 2)
dy/dt	sY(s)
 y(t)dt 0	(1/s)Y(s)