Самарасінгхе_кр

(11)

b)Табличний спосіб-таблиці 2,3

Таблиця 2 Таблиця зображення функцій виходу

Таблиця 3 Таблиця виходів для ψ

Дві таблиці відрізняються тільки з'єднанням внутрішніх кліток, тому з метою спрощення їх поєднують і приводять у вигляді так називаної сполученої таблиці переходів і виходів таблиця 4.

Змн. Арк. № докум. Підпис Дата

Таблиця 4 Таблиця переходів і виходів

c)Графічний спосіб

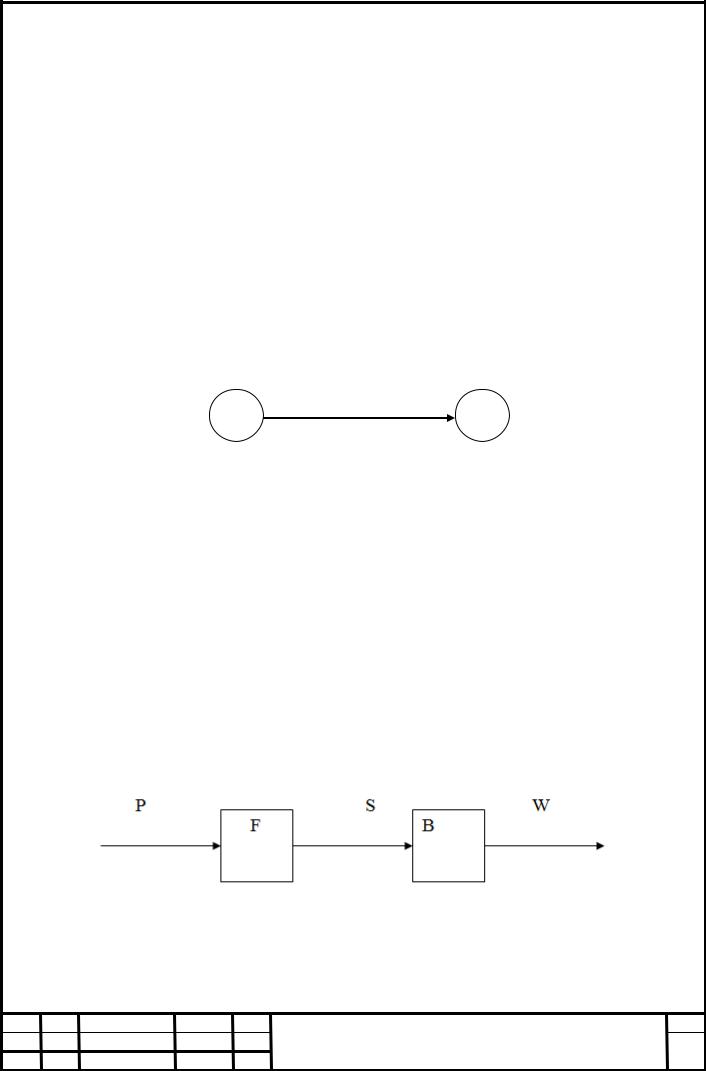
Тому що вихідний сигнал залежить і від стану і від вхідного сигналу, то вихідний сигнал приводять на ребрі графа.

Рисунок 6 Зображення функцій виходу В автоматі Мура вихідний сигнал визначається тільки станом автомата,

отже скільки завгодно довго автомат буде перебувати в деякому стані, скільки можна зчитувати його вихідний сигнал відповідному даному стану рис. 6

В автоматі Миля вихідний сигнал залежить не тільки від стану, але й від вхідного сигналу, а отже значення вихідного сигналу можна зчитувати лише в короткі інтервали часу при переходах з одного стану в інше.

1.2.2 Автомат Мура

Рисунок 7 Автомат Мура.

В автоматі Мура здійснюється відображення S →W, тобто кожній букві стану ставиться буква вихідного алфавіту рис. 7

Змн. Арк. № докум. Підпис Дата

Wi = ψ(si)

Wi (t+1)= ψ (s(t+1)) – новий вихідний символ визначається новим станом.

Завдання автомата Мура (формула 12):

A: <P, W, S, s0, φ, ψ>

(12)

В автоматі Мура ψ залежить тільки від станів.

Автомат як Мура, так і Міля задається шістьома параметрами.

P, W, S – задаються у вигляді множин

s0 – початковий стан указується як буква алфавіту S

Функція φ – задається трьома способами (розглянутими раніше):

перерахування, табличний, графічний.

Функція ψ – також може бути представлена тими ж трьома способами.

a)Перерахування (формула 13)

(13)

b) табличний спосіб Таблиця 4 Таблиця функції φ

Дана таблиця одна визначає дві функції, тому що Wi залежить тільки від Si.

Таблиця називається «відзначеною» таблицею.

Кількість W й S може бути різною, тому що різним станам може бути поставлене у відповідність та сама вихідна буква.

c)графічний спосіб рис. 8

Змн. Арк. № докум. Підпис Дата

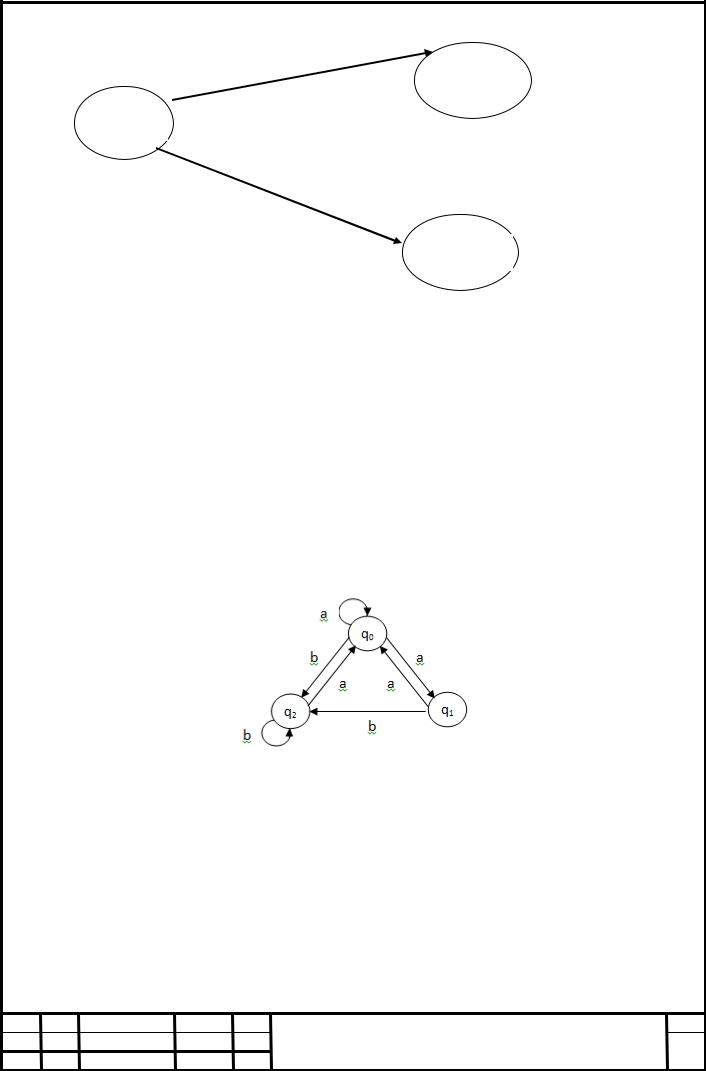
Sj / Wj

Si / Wi

Sk / Wk

Рисунок 8 Задається функція φ

1.3 Відмінність між детермінованими і недетермінованими автоматами

Відмінність між Детермінованими (ДСА) і недетермінованими (НСА)

автоматами. В детермінованих автоматах, кожен стан має лише один перехід для кожного входу. В недетермінованих автоматах вхід може призвести до одного,

більше ніж одного або зовсім без переходу для даного стану. Ця різниця важлива на практиці, але не в теорії, через існування алгоритму трансформації будь-якого НСА в складніший ДСА з однаковою функціональністю.

Рисунок 9 Недетермінований автомат К*

Концепція недетермінованого скінченного автомата легко застосовується для побудови автомата, що розпізнає об'єднання двох регулярних мов рис. 9

Нехай L1 й L2 – регулярні мови, розпізнавані кінцевими автоматами К1={Q1, A, q10, g1, F1} і К2={Q2, A, q20, g2, F2} відповідно. Нехай D1 й D2 – діаграми переходів, що визначають ці кінцеві автомати. Для побудови діаграми переходів D автомата,

що розпізнає об'єднання мов L1 й L2, поєднуємо ці діаграми в такий спосіб.

Змн. Арк. № докум. Підпис Дата

Уводимо нову вершину – стан q0. По кожній букві х вхідного алфавіту А з q0

проводимо дві дуги з надписаною буквою х; верхня дуга має своїм кінцем вершину g1(q10, х), тобто стан, у яке переходить зі свого початкового стану під впливом букви х перший автомат, а нижня – вершину g2(q20, х), тобто стан, у яке переходить зі свого початкового стану під впливом букви х другий автомат.

Початковим станом побудованого автомата вважаємо q0; множину F його

«гарних» станів визначаємо як об'єднання множин F1 й F2. Спеціально відзначимо,

що у випадку, коли хоча б в одному з автоматів К1, К2 початковий стан є

«гарним», в F варто включити стан q0. На першому такті обробки будь-якого непустого вхідного слова =х автомат має можливість переходу з q0 або по верхньої, або по нижній дузі з надписаною буквою х. Якщо реалізовано перехід по верхній дузі, то далі фактично працює автомат К1 і перевіряється приналежність слова мові L1; якщо реалізовано перехід по нижній дузі, далі працює автомат К2 і перевіряється приналежність слова мові L2; побудований автомат у результаті обробки довільного вхідного слова може виявитися в стані,

що належить підмножині F, тоді й тільки тоді, коли належить об'єднанню мов

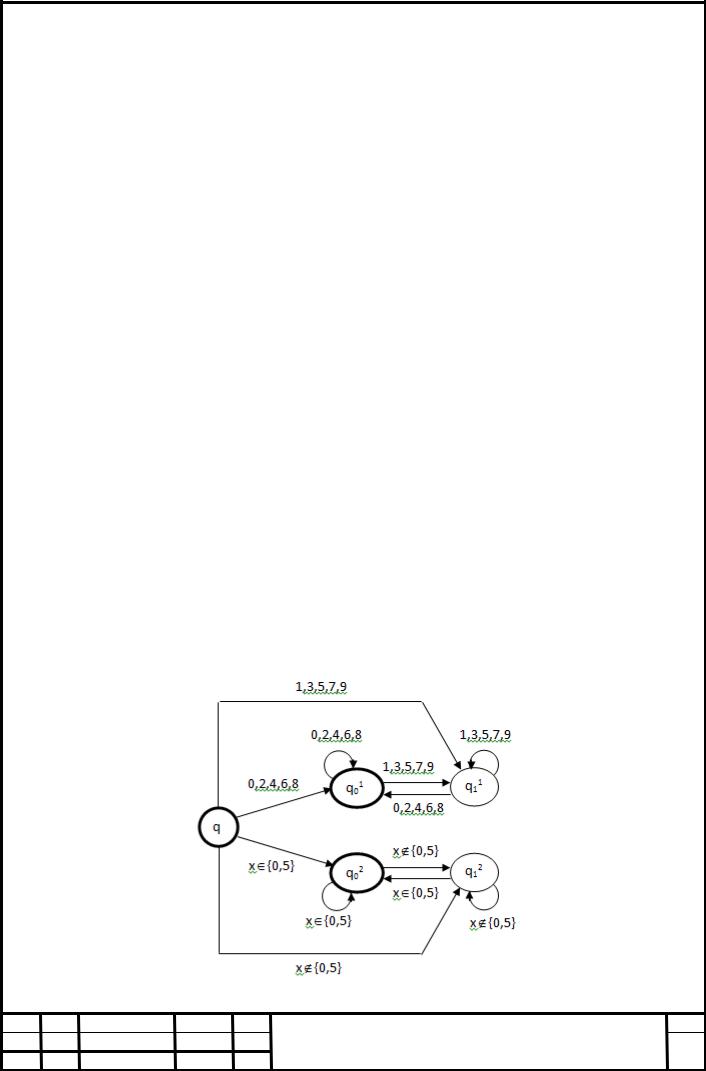
L1 й L2. Представлена діаграма переходів побудованого за викладеною схемою недетермінованого скінченного автомата, що розпізнає множину чисел, кожне з яких кратне 2 або 5 рис. 10

Змн. Арк. № докум. Підпис Дата

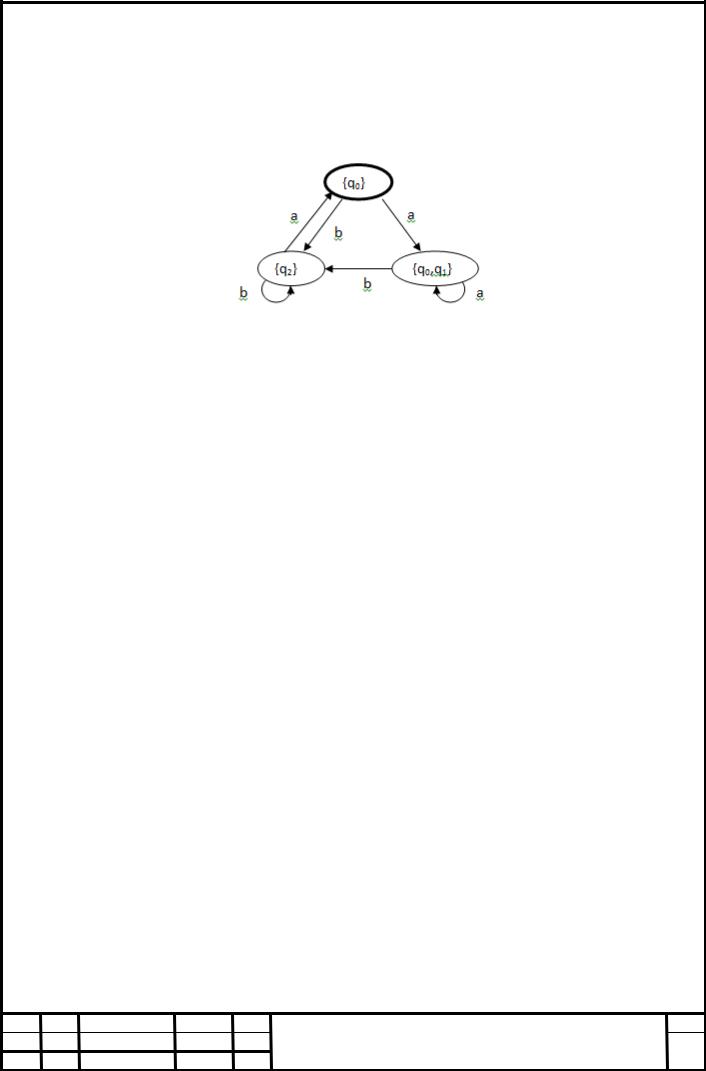
Рисунок 10 Діаграма переходів недетермінованого скінченного автомата, що розпізнає множину чисел, кожне з яких кратне 2 або 5

Рисунок 11 Детермінований скінченний автомат К

Діаграму переходів еквівалентного йому детермінований скінченного автомата К будуємо в такий спосіб рис. 11 Уводимо вершину – стан {q0}. Зі свого початкового стану q0 автомат К* по букві а або переходить в q1, або залишається в q0; по букві b автомат переходить в q2. Тому автомат К по букві а з {q0}

переходить у стан {q0, q1}, а по букві b переходить у стан {q2}. Зі станів сукупності {q0, q1} по букві а автомат К* переходить у стани тієї ж сукупності, а

по букві b як зі стану q0, так і зі стану q1 реалізується перехід в q2. Тому автомат К по букві а з {q0, q1} переходить у той же стан {q0, q1}, а по букві b переходить у стан {q2}. Зі стану q2 автомат К* по букві а переходить в q0, а по букві b –

залишається в q2. Тому автомат К по букві а з {q2} переходить в {q0}, а по букві b

– залишається в {q2}. Побудова автомата К закінчена.

Змн. Арк. № докум. Підпис Дата

2 ВИКОРИСТАННЯ КІНЦЕВИХ АВТОМАТІВ

Синтаксичний розбір здійснюється із застосуванням більш складних граматик, що забезпечують ієрархічне визначення одних правил через інші. Тому,

для побудови розпізнавачів, потужності кінцевих автоматів, використовуваних при лексичному аналізі, вже не вистачає. Необхідний більш потужний і універсальний автомат, що підтримує побудову дерева розбору і вибудовує його як зверху вниз, так і знизу вгору.

Відомо, що кінцевий автомат можна розширити додаткової робочої пам'яттю, щоб забезпечити розпізнавання ланцюжків, породжуваних практично будь-якими граматиками. Організація і поведінку такого автомата визначається класом граматик. Як визначено в класифікації Хомського, контекстно-вільних граматик можна поставити у відповідність автомат з магазинною пам'яттю

(АМП).

2.1 Розпізнавання регулярних виразів

Регулярні вирази - це потужний і (переважно) стандартизований спосіб пошуку, заміни, та лексичного аналізу тексту з складними шаблонами символів.

Хоча, синтаксис регулярних виразів досить щільний, і не схожий на звичайний код, але результат може виявитись більш читабельним ніж саморобне рішення,

що використовує велику кількість рядкових функцій. Існує навіть спосіб вставити в регулярний вираз коментарів, тому ви можете включати в них документацію.

Для будь-якої програми ключ до створення хороших регулярних виразів – це розпізнавання зразка, який містить тільки ту інформацію, яку вам треба перевіряти, так, щоб ніщо інше від вхідних значень не заважало.

Задача синтезу скінченного автомата полягає в створенні такого автомата акцептора, який би розпізнавав дану регулярну мову.

Змн. Арк. № докум. Підпис Дата

2.1.1 Мови й регулярні вирази

З погляду завдання мови важливу роль разом із граматиками, що породжують, грають регулярні вирази (regular expression). Визначення регулярного виразу співзвучно з арифметичними, логічними виразами. Дійсно, всі ці вирази будуються за строгими правилами своєї аксіоматики. Так, над арифметичними виразами існує прийнята аксіоматика алгебри, у якій введені пріоритети виконання арифметичних операцій і спосіб їхнього перевизначення за допомогою круглих дужок. Операнди в арифметичних виразах мають властивості комутативності, асоціативності й ін.

Точно так само для регулярних виразів нижче будуть уведені певні аксіоми,

наслідком яких будуть еквівалентні перетворення цих виразів.

Регулярні вирази, як й інші вирази, формально задають певні класи об'єктів,

якщо дотримуватися об’єктно-орієнтовані концепції. Класами в регулярних виразах є множина ланцюжків або мова, об'єктами якої є самі ланцюжки із символів, певного словника.

Регулярні вирази є більш компактним способом визначення підкласу

(підмножини) мов, аніж потужний апарат породжуючих граматик. Словник операцій регулярних виразів обмежений операціями конкатенації, «або» (|) і

замикання Кліні (означає ітерацію над буквою й цифрою або замикання Кліні).

Як предметне позначення деякого об'єкта з мови, приведемо приклад ідентифікатора, що представляє певним чином побудований ланцюжок символів – букв (Б) або цифр (Ц), причому першим символом у ланцюжку є буква, а потім послідовність букв і цифр. граматики, що породжують, у цьому випадку визначають цю конструкцію як

G [<ідентифікатор>]:

VT = {Б, Ц}, VN = {<ідентифікатор>, <хвіст ідентифікатора>, <Б Ц>}

P:

1.< ідентифікатор >→ Б < хвіст ідентифікатора >

2.< хвіст ідентифікатора >→<Б Ц>< хвіст ідентифікатора > | L

Змн. Арк. № докум. Підпис Дата

<БЦ>→Б | Ц

Мова, породжувана цією граматикою L (G[<ідентифікатор >]) і є ідентифікатором. Ця ж мова ідентифікаторів можна задати простіше у

вигляді простої формули 14

R1 = Б (Б | Ц)*,

(14)

відповідно мова, визначена формулою або регулярним виразом R1

визначена як множина L(R1) = {Б (Б|Ц)*}.

Таке просте завдання мови не вимагає компонентів VN, P, Z й у загальному самої граматики G[Z]. Необхідно тільки задати словник S =VT і саме вирази

(формулу) R, що визначає мова.

Так само просто можна визначити цілі без знака, як нескінченну ітерацію цифр позиційної системи числення R2 = a b*, де a – це всі цифри без 0 – [1 – 9], b –

всі цифри – [0 – 9].

Відповідно мова цілих представлена дуже просто – L(R2) = {ab*}.

Однак, так просто можна задати далеко не всі синтаксичні конструкції мови на відміну від граматик, що породжують, для яких немає обмежень в ієрархії

(класифікації) Хомського. Обмеженість язикових конструкцій, породжуваних регулярними виразами, і є плата за простоту подання виразів.

Регулярні вирази широко використаються у всіх процесорах, у яких потрібен шаблоновий-орієнтований пошук. У першу чергу – це лексичні аналізатори. Для виділення шаблонів – ідентифікаторів, числових констант,

ключових слів і т.д. використають регулярні вирази. Наприклад, у системі LEX

генератора лексичних аналізаторів всі шаблони визначаються регулярними виразами, а генератор в LEX генерує ефективний скінченний автомат, що розпізнає шаблони.

Змн. Арк. № докум. Підпис Дата

2.1.2 Автоматні граматики й регулярні вирази

Розглянемо мову L = {anbn | nі1}. Множина рядків цієї мови є підмножиною рядків мови, певного регулярного виразу R = aa*bb*. Дійсно в L всі рядки складаються тільки з тих послідовностей a й b, у яких символи a повторюються один і більше раз, за ними треба послідовність символів b, які точно повторюють попереднє їм кількість символів а. Для L(R) – ланцюжка включають всі послідовності символів а, за яких треба b, причому й таких у тому числі послідовностей, де кількість може бути й не рівним b. Тому в загальному випадку регулярний вираз R відповідає мові, породжуваному граматикою G[I]; такому що

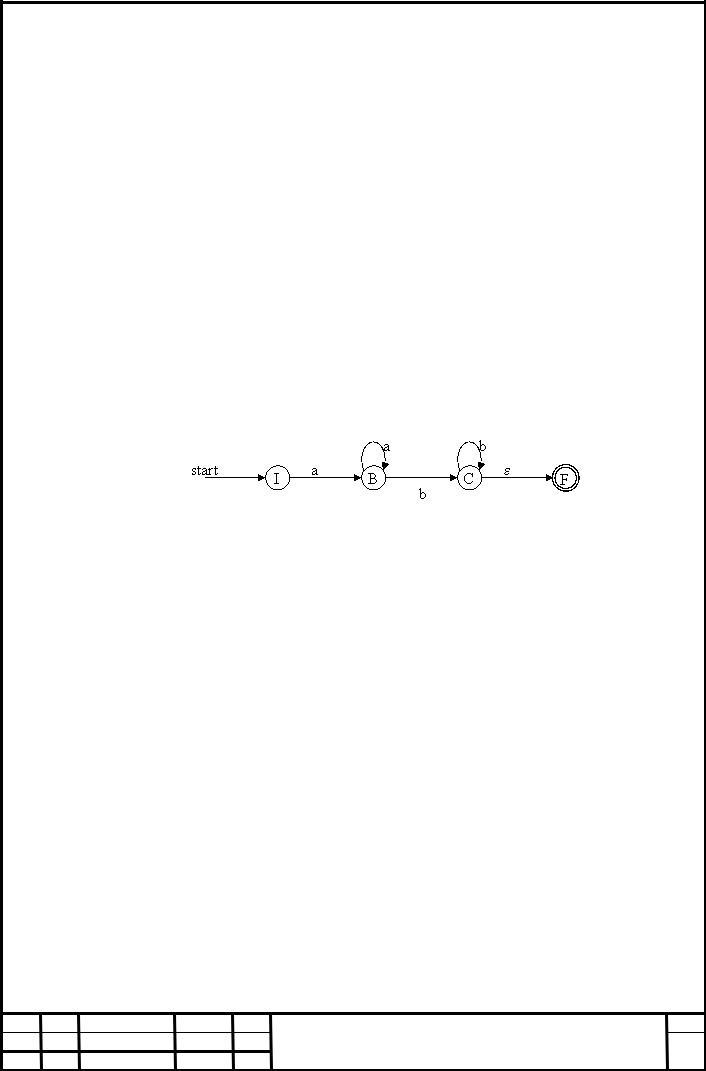
L (G[I]) = {anbm| n, m і 1} із графом переходів представленим на рис.12

Рисунок 12 Регулярний вираз R

Регулярний вираз R відповідний мові, породжуваної граматики G[I] із

графом переходів

Відповідна автоматна граматика легко підбирається по графу G[I]:

I→a

B→Ab | b

C→a | e

У такий спосіб автоматна граматика G[I] породжує ту ж мову, що й мова

L(R), визначений регулярним виразам L(R) = L (G[I]). У цьому випадку можна говорити про еквівалентності регулярного виразу R й автоматної граматики G[I].

Тому автоматну граматику G[I] ще називають регулярною, що й було зроблено в класифікації Хомського.

Змістовними прикладами використання регулярного виразу (РВ) є

побудовані на принципах РВ сучасні лексичні аналізатори. На поняттях РВ і