Лабораторная работа № 6

Тема: Математическая обработка экспериментальных данных. Построение множественной линейной регрессии

Цель работы: Приобретение навыков построения множественных линейных регрессий на основе экспериментальных данных, оценка параметров множественной линейной модели, зоны ее надежности и прогноза

Краткие теоретические сведения

Объект исследования – это объект любого характера (технического, социального, экономического, астрономического и т.д. и т.п.), который изучается экспериментальным путем.

Эксперимент – это специальным образом спланированная и организованная процедура изучения некоторого объекта исследования, при которой на этот объект оказывают запланированные воздействия и регистрируют его реакции на эти воздействия.

Факторы – это воздействия на объект.

Откликами объекта исследования называют его реакции на воздействия

Экспериментальные данные – все исходные и выходные числове данные эксперимента, сведенные в таблицу экспериментальных данных.

Обработка экспериментальных данных – различные методы построения математической модели объекта по таблице экспериментальных данных.

Регрессионный анализ – наиболее распространенный метод обработки данных, который включает в себя метод наименьших квадратов. При регрессионном анализе таблица экспериментальных данных обычно отражается алгебраическими степенными полиномами, которые называют полиномами или уравнениями регрессии. Отсюда термины – задача регрессии, коэффициенты регрессии и т.п. Сам термин регрессия отражает тот факт, что с увеличением степени полинома точность отражения таблицы эспериментальных данных обычно возрастает, а ошибка отражения соответственно уменьшается, регрессирует.

Управляемые факторы - это такие воздействия на объект исследования, численные значения которых определяются и контролируются самим экспериментатором.

Активный эксперимент – это эксперимент, в котором задействованы только управляемые факторы.

Контролируемые факторы - это такие воздействия на объект исследования, численные значения которых экспериментатором не устанавливаются, но значения их исследователь может измерять, контролировать и фиксировать.

Пассивный эксперимент – это эксперимент, в котором задействованы только контролируемые факторы.

Активно-пассивный (или пассивно-активный) эксперимент – это совмещение обоих видов эксперимента.

Основным «рабочим инструментом» и эксперимента и обработки экспериментальных данных является численное значение факторов воздействия

и откликов объекта исследования, т.е. число. Какова ни была бы природа факторов и откликов, включая в том числе эмоции или впечатления, они должны быть выражены количественно, числом.

Числа при экспериментировании получают тремя способами:

- подсчетом,

- измерением,

- методом экспертных оценок.

Статистический ряд.

Пусть изучается некоторая случайная величина X, закон распределения которой неизвестен. С этой целью над случайной величиной Х производится ряд независимых опытов (измерений). Результаты измерений представляют в виде таблицы, состоящей из двух строк, в первой из которых указываются номера измерений i, а во второй - результаты измерений x_i :

i	1	2	3	4	. . .	n
xi	x1	x2	x3	x4	. . .	xn

Таблицу, в которой содержатся номера и результаты измерений, в математической статистике называют статистическим рядом. На основании статистического ряда можно построить статистическую функцию распределения случайной величины Х.

Статистическая совокупность. Гистограмма.

При большом числе наблюдений представление результатов наблюдений в виде статистического ряда бывает затруднительным. В таких случаях производят подсчет результатов наблюдений, попадающих в определенные группы, и составляют таблицу, в которой указывают группы и частоту получения результатов наблюдения в каждой группе. Совокупность групп, на которые разбивают результаты наблюдений и частоты получения результатов наблюдений в каждой группе, называют статистической совокупностью.

Графическим изображением статистической совокупности является так называемая гистограмма. Она строится следующим образом: по оси абсцисс откладывают интервалы, соответствующие группам совокупности, и на каждом из них, как на основании строится прямоугольник, площадь которого равна частоте данной группы - тогда полная площадь ее равна единице.

Числовые характеристики статистического распределения.

Основными числовыми характеристиками случайной величины является математическое ожидание и дисперсия. Математическое ожидание характеризует среднее значение, около которого группируются возможные значения случайной величины, а дисперсия характеризует степень разбросанности этих значений относительно среднего.

Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. Термин «вариация» имеет латинское происхождение - variatio, что означает различие, изменение, колеблемость. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение.

Для измерения вариации признака используют как абсолютные, так и относительные показатели.

К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию.

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др.

Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:

R=X_max-X_min.

Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели.

Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.

Формула среднего линейного отклонения (простая)

.

Формула среднего линейного отклонения (взвешенная)

.

При использовании показателя среднего линейного отклонения возникают определенные неудобства, связанные с тем, что приходится иметь дело не только с положительными, но и с отрицательными величинами, что побудило искать другие способы оценки вариации, чтобы иметь дело только с положительными величинами. Таким способом стало возведение всех отклонений во вторую степень. Обобщающие показатели, найденные с использованием вторых степеней отклонений, получили очень широкое распространение. К таким показателям относятся среднее квадратическое отклонение и среднее квадратическое отклонение в квадрате , которое называют дисперсией.

Средняя квадратическая простая

.

Вибіркове середнє (точкову оцінку математичного сподівання) n резульнатів спостережень x_i ( i = 1,2,…, n)

.

Средняя квадратическая взвешенная

.

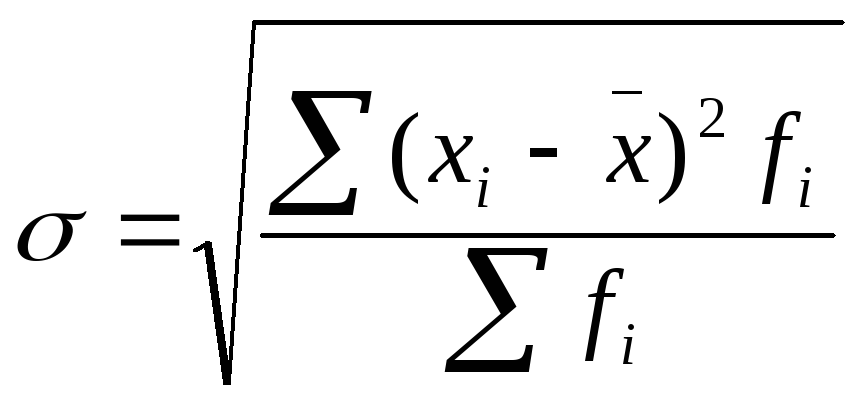Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины.

Формулы дисперсии взвешенной и простой :

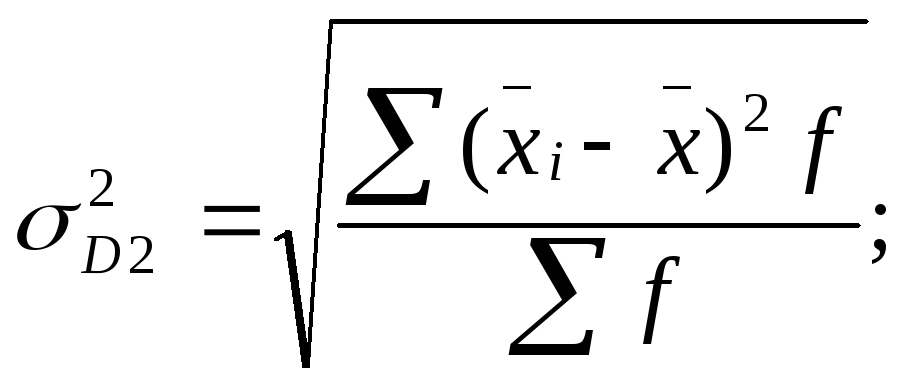
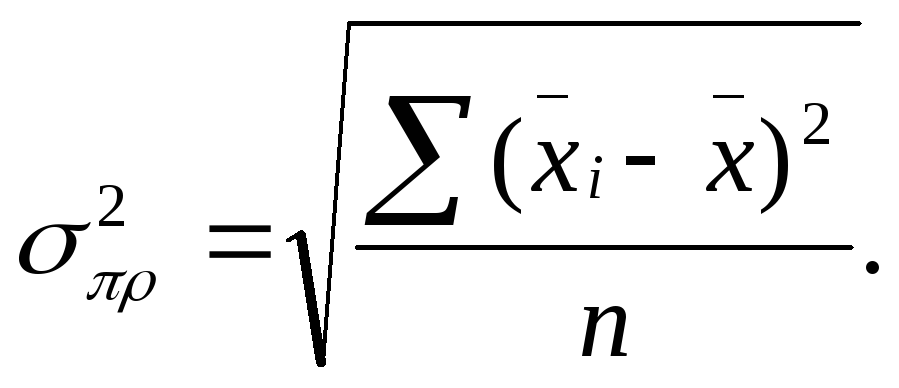
Вибіркова дисперсія (незміщена точкова дисперсія) та точкова оцінка середнього квадратичного відхилення

; .

Оцінка середнього квадратичного відхилення результату виміру

.

Расчет дисперсии можно упростить. Для этого используется способ отсчета от условного нуля (способ моментов), если имеют место равные интервалы в вариационном ряду.

Мода в теории вероятностей и математической статистике, одна из характеристик распределения случайной величины. Для случайной величины, имеющей плотность вероятности р(х), Модой называется любая точка, в которой р(х) имеет максимум. Наиболее важным типом распределений вероятностей являются распределения с одной модой (унимодальные).  

Мода представляет собой максимально часто встречающееся значение переменной (иными словами, наиболее «модное» значение переменной), например, популярная передача на телевидении, модный цвет платья или марка автомобиля и т. д, Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).

Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»).

Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах, особенно для целей сравнения колеблемости различных признаков одной и той же совокупности или для сравнения колеблемости одного и того же признака в нескольких совокупностях.

Данные показатели рассчитываются как отношение размаха вариации к средней величине признака (коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака (линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака (коэффициент вариации) и, как правило, выражаются в процентах.

Формулы расчета относительных показателей вариации:

; ;.

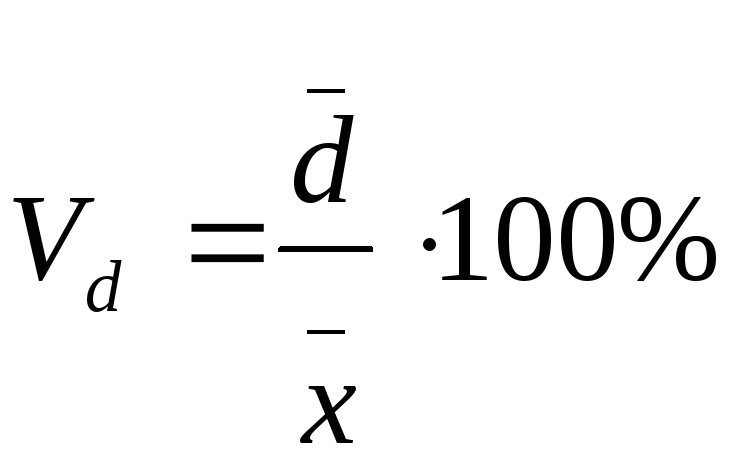где V_R - коэффициент осцилляции;

V_d - линейный коэффициент вариации;

V_ - коэффициент вариации.

Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака.

В статистической практике наиболее часто применяется коэффициент вариации. Он используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

У разі побічних вимірів іскоме значення випадкової величини, яка вимірюється, обчислюється за результатами прямих вимірів величин, зв'язаних з іскомою визначеною функціональною залеж­ністю.

Окремий результат при багаторазовому прямому вимірюванні фізичної величини через наявність випадкових похибок представ­ляє собою випадкову величину.

Нагадаємо деякі відомості з теорії ймовірностей. Під випад­ковою розуміють величину, яка в результаті досліду з випадко­вим результатом приймає те або інше значення. Оскільки законо­мірностей у появі цих значень немає, аналіз таких величин може виконуватися тільки методами теорії ймовірностей і математич­ної статистики. Для характеристики випадкової величини необ­хідно знати сукупність значень цієї величини, а також імовірно­сті, з якими ці значення можуть з'явитися.

Випадкова величина називається дискретною, якщо множина її можливих значень кінцева або лічильна. Неперервні (недискретні) випадкові величини характеризуються тим, що множина їх можливих значень нелічильна.

Законом розподілу випадкової величини називається будь-яке правило, яке дозволяє знаходити ймовірності можливих подій, зв'я­заних з випадковою величиною.

Найбільш загальною формою закону розподілу випадкової ве­личини є функція розподілу, яка представляє собою ймовірність того, що випадкова величина X прийме значення менше, ніж задане х:

F(x)=P{X<x}.

Якщо функція розподілу F(x) випадкової величини Х при будь-якому х неперервна і, крім того, має похідну F'(x) будь-де, крім, можливо, окремих точок, то випадкова величина є неперервною.

Щільністю ймовірності неперервної випадкової величини X називається похідна функції розподілу f(x)=F'(x).

Найбільш розповсюдженим для неперервних випадкових ве­личин є нормальний розподіл (розподіл Гаусса) зі щільністю ймо­вірності

,

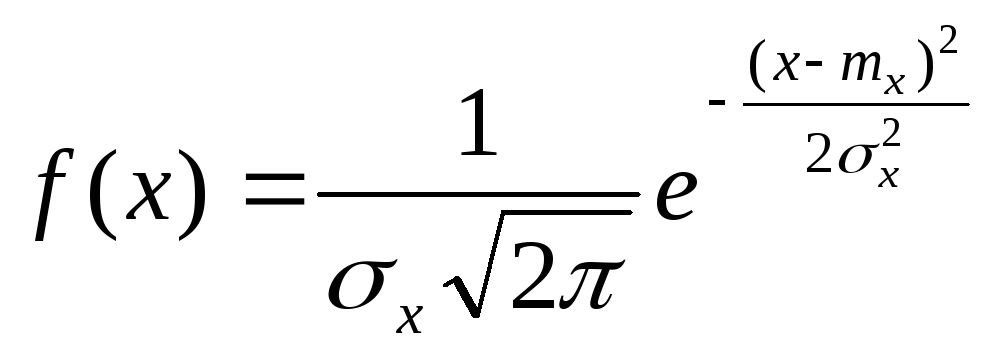де m_х- математичне сподівання (середнє значення) випадкової величини X.

Нормально розподілені випадкові величини часто зустрічають­ся на практиці. Так, випадкові похибки багатократних вимірів зазвичай розподілені за нормальним законом, навіть коли закони розподілу ймовірностей складових відрізняються від нормального.

Крім того, історично склалося так, що багато статистичних критеріїв, методів і оцінок розроблені тільки для нормального по­чаткового розподілу. Тому при первинній обробці експеримен­тальних даних перевіряють нормальність закону розподілу резуль­татів спостережень.

Перевірку нормальності цього закону (розподілу результатів спостережень) виконують за критерієм Пірсона (критерієм ² ). Від­повідно до цього критерію спочатку обчислюють значення ² :

,

де m - кількість підінтервалів (кліток), на які розбивається інтер­вал [x_min,x_max]; x_min і x_max - відповідно мінімальне і максимальне значення випадкової величини X; n_j- абсолютна частота в j-му підінтервалі (кількість значень випадкової величини, які попада­ють у j-й підінтервал); р_j - ймовірність того, що значення випадко­вої величини X попадають у j-й підінтервал.

Кількість підінтервалів (кліток), на які розбивається інтервал [x_min, x_max], може бути визначена за наступними формулами:

m = log₂ n+1 =3.31lg n+1(формула Старжеса) або m = lg n(форму­ла Брукса і Карузера).

Імовірність того, що значення випадкової величини X попа­дають у j-й підінтервал, може бути визначена як

,

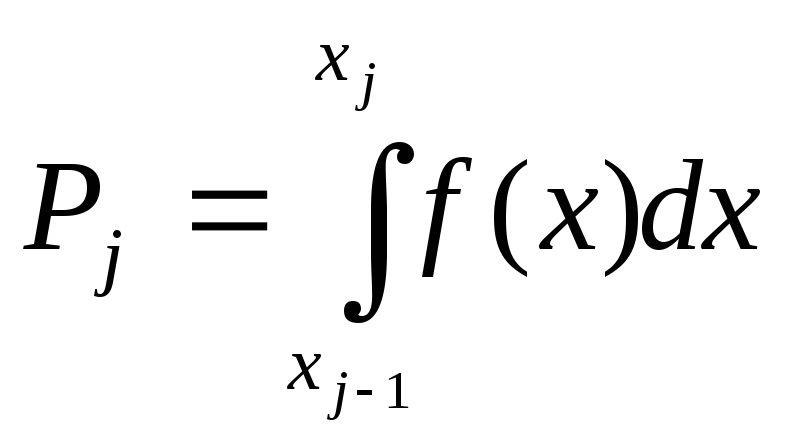де x_j-1 і x_j- ліва і права границі j-го підінтервалу.

Після цього в залежності від рівня значимості  та кількості ступенів свободи за таблицею верхніх 100%-х точок розподілу ² (дод. А) знаходять значення . Якщо² <, то з імовірністю 1- можна прийняти гіпотезу, що закон розподілу результатів спо­стережень є нормальним, при ² > - цю гіпотезу потрібно від­кинути.

Кількість ступенів свободи v визначається як

v = m-k-l,

де k - кількість параметрів, від яких залежить закон розподілу. Для нормального розподілу k = 2.

Якщо із заданою довірчою ймовірністю закон розподілу резуль­татів спостережень можна вважати нормальним, для цього ж зна­чення ймовірності знаходять довірчу похибку результату виміру та довірчий інтервал для середнього квадратичного відхилення.

Завдяки випадковому характеру похибки оцінки пара­метра  для конкретизації точності наближеної рівності не­обхідно мати ймовірність р_Д того, що перейде деяку грани­цю >0:

.

Інтервал від - до +, в якому з імовірністю р_Д знаходить­ся справжнє значення , називається довірчим інтервалом, а його границі - довірчими границями, ймовірність р_Д - довірчою ймовір­ністю.

Величина = 1-р_Д в загальному випадку називається рівнем значимості. Під рівнем значимості якої-небудь статистичної гіпо­тези розуміють найбільшу ймовірність , з якою ця гіпотеза може дати помилковий результат.

Для нормальної генеральної сукупності (1 - )%-й довірчий ін­тервал точкової оцінки математичного сподівання визначається як

,

де t_n-1 - квантіль t-розподілу Стьюдента, визначається за табли­цею верхніх 100%-х точок t-розподілу Стьюдента (дод. Б) в за­лежності від рівня значимості /2 та кількості ступенів свободи v, v = n-1/

Величину розглядають як довірчу похибку резуль­тату виміру. Вона зменшується зі збільшенням n.