Выборочная средняя

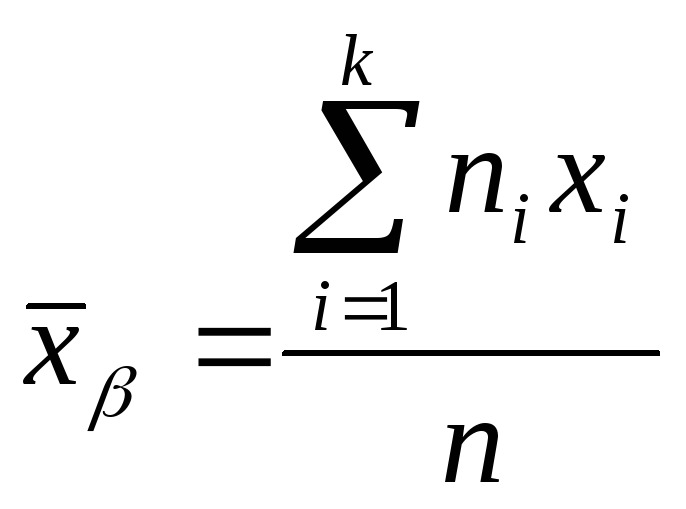,n – объем выборки.

Если дано распределение непрерывной случайной величины, то вместо х_i берут середину интервала (х_i,…, х_i+1), то есть .

Выборочная и исправленная дисперсия

Чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения вводят выборочную дисперсию.

Выборочной дисперсией D_B называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

.

Часто для вычисления выборочной дисперсии используют следующую формулу:

.

Выборочная дисперсия имеет систематическую ошибку, приводящую к уменьшению дисперсии. Чтобы это устранить, вводят поправку, умножая D_B на n/(n-1). Получают исправленную дисперсию:

или:

.

На практике используют другую, равносильную ей формулу:

.

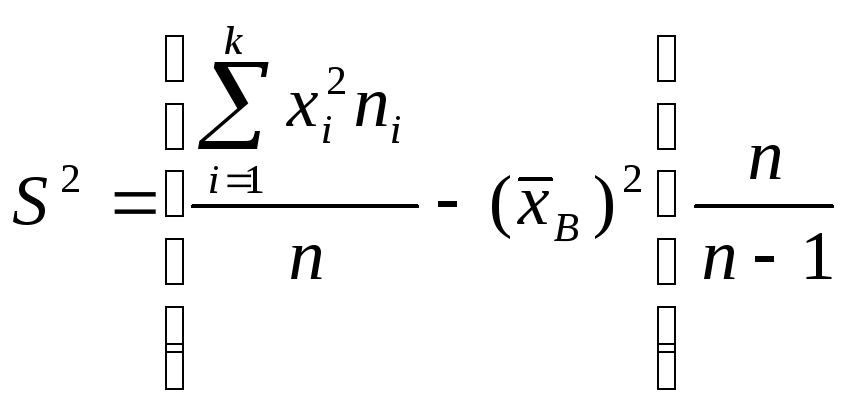Мода

Модой М₀ называют значение признака, которое имеет наибольшую частоту (n_i = max).

Медиана

Медианой m_e называют значение признака, которое делит статистическое распределение на две равные части:

m_e = x_k+1, если n = 2k + 1,

m_e = (x_k + x_k+1)/2, если n = 2k.

Выборочное среднее квадратическое отклонение

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

=

Исправленное среднее квадратическое отклонение:

S =

Коэффициент вариации

Коэффициентом вариации V называется отношение выборочного среднего квадратического отклонения к выборочной средней, выраженное в процентах:

V = .

Коэффициент вариации служит для сравнивания меры рассеяния значений признаков около выборочной средней в разных выборках.

Статистические оценки параметров распределения

Пусть требуется изучить количественный признак генеральной совокупности. Пусть удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.

Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то требуется оценить, то есть приближенно найти математическое ожидание (а) и среднее квадратическое отклонение (δ), так как эти два параметра полностью задают нормальное распределение. Если же известно, что признак имеет распределение Пуассона, то необходимо оценить параметр “”, которым оно определяется.

Обычно оцениваемый параметр выражают через данные выборки, например, через значения количественного признака х₁, х₂,…,х_n, полученные в результате наблюдений.

Статистической оценкой неизвестного параметра теоретического распределения называют его приближенное значение, зависящее от данных выборки (х₁, х₂,…, х_k; n₁, n₂ ,…,n_k), то есть некоторую функцию этих величин.

x₁, х₂, …,х_k - значения признака; n₁, n₂, …, n_k - частоты. Статистическая оценка является случайной величиной.

Пусть Θ – оцениваемый параметр, Θ* - его статистическая оценка. Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ - Θ*|. Другими словами, если δ >0 и |Θ - Θ*|< δ, то чем меньше δ, тем оценка точнее. Таким образом, величину |Θ - Θ*| называют точностью оценки, а число δ характеризует точность оценки.

Чтобы оценка Θ* имела практическое значение, она не должна содержать систематической ошибки и вместе с тем иметь возможно меньшую дисперсию. При этом если оценка Θ* дает приближенное значение Θ с избытком (Θ* > Θ), то и математическое ожидание (среднее значение) M(Θ*)>Θ; если же Θ* дает оценку с недостатком (Θ* < Θ), то и M (Θ*) < Θ. На основании этого делаем вывод, что соблюдение требований M(Θ*) = Θ гарантирует от получения систематических ошибок.

Оценка параметра называется несмещенной, если ее математическое ожидание M (Θ*) равно оцениваемому параметру Θ, то есть M (Θ*) = Θ и смещенной, если M(Θ*)  Θ.

Оценка Θ* называется эффективной, если при заданном объеме выборки “n” она имеет наименьшую дисперсию.

Оценка Θ* называется состоятельной, если при любом δ > 0:

lim P (|Θ - Θ*|< δ) = 1, то есть оценка Θ* сходится по вероятности к Θ.

Теорема1. Выборочная средняя является несмещенной и состоятельной оценкой математического ожидания.

является и эффективной оценкойM (Х).

Теорема 2. Исправленная выборочная дисперсия является несмещенной и состоятельной оценкой дисперсии D(Х).