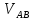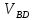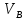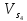1 Структурный и кинематический анализ рычажного механизма вытяжного пресса.

Исходные данные: Частота вращения кривошипа .

;

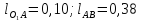1.3. Структурный анализ механизма

Число подвижных звеньев n = 5. Число кинематических пар V класса ( низших)

Число кинематических пар четвертого класса(высших)

Степень подвижности механизма находим по формуле Чебышева:

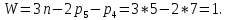
Входным (ведущим) звеном является кривошип 1, выходным звеном – ползун 5, совершающий возвратно-поступательное движение.

Проводим разложение механизма на структурную группу рис(1.1). Формула строения механизма имеет вид:

Итак, имеем механизм 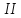класса, состоящий из начального механизмакласса и двух структурных групп изкласса.

1.4 Построение планов положение механизма

Назначаем масштабный коэффициент длин

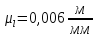
Находим размеры звеньев в выбранном масштабе:

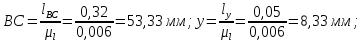
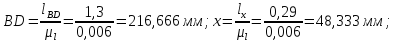
Строим 12 наложенных один на другой планов механизма по двенадцати равноотстоящим положениям кривошипа. В качестве нулевого принимаем положение , при котором пуансон 5 (точка D) занимает крайнее верхнее положение.

1.5. Построение планов скоростей

Находим угловую скорость кривошипа 1 :

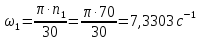
Скорость точки A кривошипа 1 (и шатуна 2) :

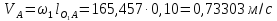
Вектор направлен перпендикулярно осикривошипа в сторону его вращения.

Назначаем масштабный коэффициент планов скоростей

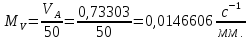
Для определения скорости точки B, используем векторное уравнения:

В этих уравнениях 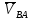– вектор скорости вращение точкиB вокруг A; перпендикулярен линии AB. Скорость точки С равна нуля, поэтому на плане скоростей точка с расположена в полюсе. Вектор 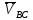перпендикулярен линииBC.

Скорость точки D находим , используя уравнение

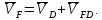
Положение точек 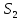на планах скоростей находим из пропорций :

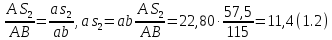
Положение точек 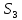на планах скоростей находим из пропорций :

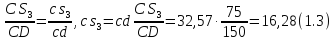
Результаты измерений величин, входящих в выражения (1.1) и (1.2) и (1.2) сводим в таблицу 1.1.

Из плана скоростей находим:

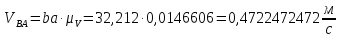
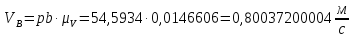
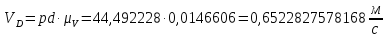
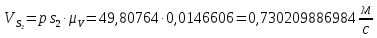
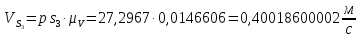
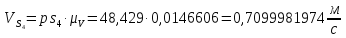
Угловую скорость шатуна 2, 4 и коромысла 3 находим по формулам:

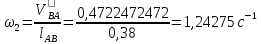
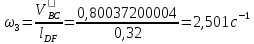
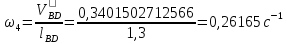
Результаты сводим в таблицу 1.2.

Таблица 1.2

Значение абсолютных и относительных скоростей (м/с) и угловые скорости (

Отрезок	Положение механизма
	0	1	2	3	4	5	6	7	8	9	10	11
	0,65	0,10	0,28	0,47	0,65	0,76	0,06	0,24	0,63	1,24	0,86	0,37
	0,68	0,35	0,46	0,61	0,73	0,78	0,33	0,47	0,34	0,84	0,90	0,66
	0,32	0,15	0,22	0,60	0,40	0,42	0,03	0,12	0,31	0,67	0,57	0,29
	0,15	0,80	0,78	0,66	0,47	0,24	0,69	0,53	1,18	1,38	0,62	0,19
	0,11	0,13	0,30	0,37	0,34	0,21	0,05	0,01	0,00	0,32	0,58	0,39
	0,64	0,18	0,45	0,33	0,80	0,83	0,07	0,27	0,63	1,40	1,19	0,58
	0,64	0,15	0,34	0,47	0,71	0,79	0,05	0,24	0,00	1,31	0,96	0,45
	0,39	2,10	2,06	1,73	1,24	0,63	1,81	1,41	3,11	3,63	1,63	0,51
	1,99	0,55	1,39	1,03	2,50	2,60	0,21	0,84	1,97	4,39	3,71	1,83
	0,08	0,10	0,23	0,29	0,26	0,16	0,04	0,01	0,00	0,24	0,44	0,30