Лабораторная работа № 11

Изучение вынужденных колебаний в колебательном контуре

1. Цель работы: изучение зависимости тока в колебательном контуре от частоты источника, включенного в контур, измерение резонансной частоты контура.

2. Вынужденные колебания в rlc-контуре.

Рассмотрим процессы, протекающие в колебательном контуре, подключенном к источнику, напряжение которого изменяется по гармоническому закону

. (11.1)

Мгновенные значения тока и напряжений удовлетворяют закону Кирхгофа, установленному для цепей постоянного тока. В любой момент времени сумма падений напряжения на элементах цепи равна U (рисунок 11.1)

(11.2)

или . (11.3)

Ток в контуре . (11.4)

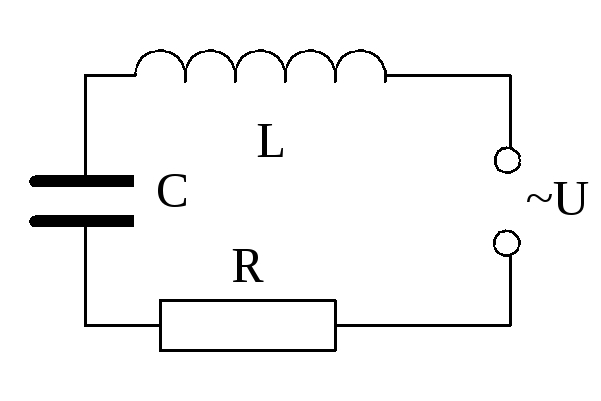
Рисунок 11.1 – Колебательный контур

Подстановка выражений (11.3) и (11.4) в (11.2) дает

. (11.5)

Разделим это уравнение на LC, и, введя обозначения

, где ₀ – собственная частота колебаний,

– коэффициент затухания,

получим дифференциальное уравнение

. (11.6)

Решение этого уравнения, то есть закон изменения напряжения на конденсаторе с течением времени, есть сумма полного решения однородного уравнения (11.7) и частного решения уравнения (11.6)

. (11.7)

Однородное уравнение (11.7) имеет решение

, (11.8)

являющееся уравнением затухающих колебаний. Затухание определяется членом . За время, равное времени релаксации амплитуда колебаний уменьшается в e=2,72 раз. При этом, затухание в колебательном контуре связано с превращением энергии колебаний в тепло на сопротивлении R. При составляющая решения уравнения (11.6) обратится в нуль, следовательно, она отражает переходный процесс, определенный начальными условиями и параметрами контура. Установившиеся колебания в цепи происходят с частотой  и сдвигом по фазе . Поэтому решение ищем в виде

, (11.9)

где и  подлежат определению.

Подстановка (11.9) в (11.6) дает

; (11.10)

. (11.11)

Видно, что амплитуда и фаза напряжения на конденсаторе зависят от соотношения частоты источника  и частоты ₀. Ток в контуре

, (11.12)

где .

Амплитуда тока в контуре также зависит от соотношения частот  и ₀

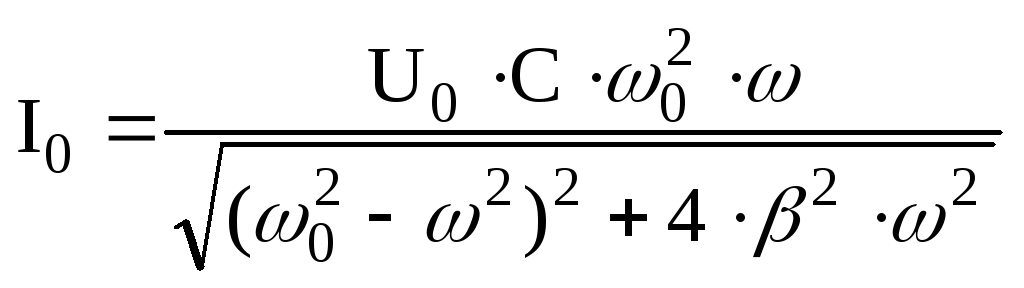. (11.13)

График зависимости от представлен на рисунке 11.2.

Рисунок 11.2 – Зависимость тока от соотношения частот

Из графика видно, что амплитуда тока резко возрастает при приближении циклической частоты  источника к частоте ₀. Это явление называется резонансом, а кривые – резонансными кривыми. Величина максимума зависит от ; при увеличении  максимальное значение тока уменьшается, ₁ определяет разность фаз колебаний тока и напряжения внешнего источника

. (11.14)

График зависимости ₁ от частоты представлен на рисунке 11.3.

Величина , где , называется добротностью колебательного контура. Добротность контура связана с остротой резонансных кривых. Найдем ширину резонансной кривой на высоте(рисунок 11.4). Из формулы (11.13) следует, что максимальное значение тока определяется выражением:

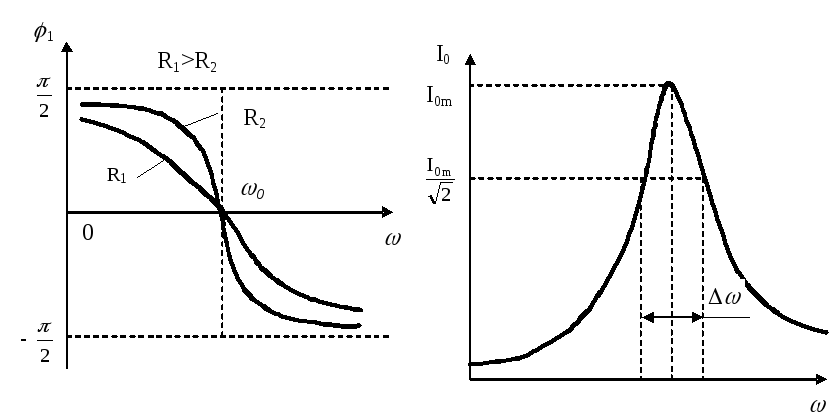
Рисунок 11.3 – График зависимости 1 от частоты

Рисунок 11.4 – Зависимость тока от частоты

(11.15)

При формула (11.15) запишется

. (11.16)

Выражение (11.16) можно преобразовать к виду или . Величина , а вблизи резонанса . После подстановки получим .

. (11.17)

При малом затухании и относительная ширина резонансной кривой численно равна величине обратной добротности контура. Если известны параметры контура, добротность может быть рассчитана по соотношению

(11.18)

Принципиальная электрическая схема лабораторной установки приведена на рисунке 11.5. Колебательный контур состоит из катушки L, магазина емкостей – С, переменного сопротивления R и сопротивления R₁. Напряжение на сопротивлении R₁, пропорциональное току в контуре, подается на вход Y электронного осциллографа. Для снятия резонансных кривых, изменяя частоту звукового генератора, определяют зависимость при различных сопротивлениях контура R.

Для измерения сдвига фаз ₁ можно использовать фигуры Лиссажу, получаемые на экране осциллографа. Пусть имеются два синусоидальных напряжения одинаковой частоты . Подадим эти напряжения на вертикальные и горизонтальные пластины осциллографа. Смещение луча под действием этих напряжений пропорционально напряжениям по горизонтали , а по вертикали , где  – сдвиг фаз между напряжениями, – амплитуды смещения луча, пропорциональные амплитуде напряжения и коэффициентам усиления соответствующих каналов осциллографа. Исключая время, получим

. (11.19)

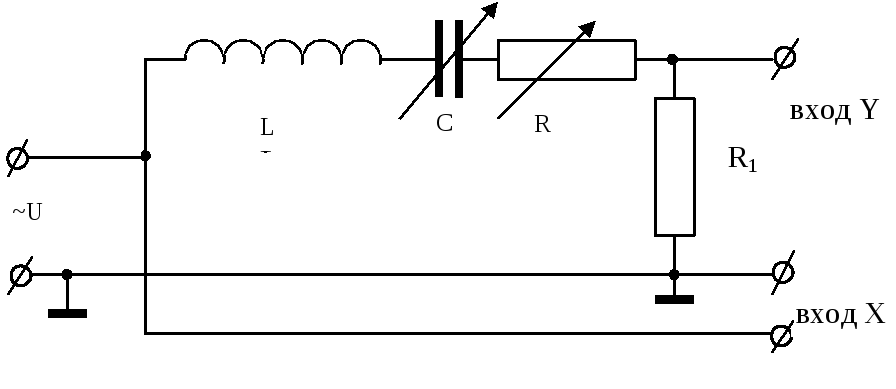
Рисунок 11.5 – Принципиальная электрическая

схема лабораторной установки

Выражение (11.19) – уравнение эллипса, описываемого электронным лучом на экране осциллографа. Выберем коэффициенты усиления вертикального и горизонтального каналов осциллографа такими, чтобы . В этом случае

. (11.20)

Уравнение (11.20) – уравнение эллипса, оси которого составляют угол  с осями координат. При =0 эллипс вырождается в прямую , при – в круг радиуса . Для точки М эллипса (рисунок 11.6) Y=X, следовательно, , а уравнение (11.20) для этой точки примет вид

;

;

.

Отсюда

. (11.21)

Рисунок 11.6 – Эллипс напряжений

Аналогично для точки N эллипса (рисунок 11.6) Y=–X, получим

. (11.22)

Из выражений (11.21) и (11.22) получим

. (11.23)

Таким образом, для измерения сдвига фаз между напряжениями одинаковой частоты достаточно измерить полуоси а и b эллипса, вписанного в квадрат на экране осциллографа.