
- •В.Н. Седалищев
- •Часть 1 фопи-1
- •Лабораторная работа №1 «Исследование термоэлектрического эффекта»
- •Пример выполнения расчетной части в среде MathCad
- •Лабораторная работа №2 «Исследование температурной зависимости электрического сопротивления металлов и полупроводников»
- •Пример выполнения расчетной части в среде MathCad
- •Лабораторная работа №3 «Исследование магнитных цепей»
- •Пример выполнения расчетной части в среде MathCad
- •Контрольные вопросы:
- •Пример выполнения расчетной части в среде MathCad
- •Литература
- •Приложение Оценка истинного значения измеряемой величины с помощью интервалов
Министерство образования Российской Федерации
Алтайский государственный технический университет
им. И.И.Ползунова
Е.М. Патрушев
В.Н. Седалищев
Методические указания к лабораторным и практическим работам по курсу
«Физические основы получения информации»
для студентов специальности 190900
«Информационно-измерительная техника и технологии»
Часть 1 фопи-1
Барнаул 2002г.
УДК 53.08(075.5)
Патрушев Е.М., Седалищев В.Н. Методические указания к лабораторным и практическим работам по курсу «Физические основы получения информации» для студентов специальности 190900 «Информационно-измерительная техника и технологии» Часть 1 / АлтГТУ им. И.И.Ползунова. - Барнаул: Изд-во АлтГТУ, 2002.- 56с.
Методические указания содержат краткие теоретические сведения, задания к лабораторным и практическим работам, требования к оформлению отчетов.
Рассмотрены и одобрены
на заседании кафедры
«Информационные технологии»
Протокол №1 от 1 ноября 2002г.
Рецензент: к.т.н., доцент Лукьянов В.Г.
Лабораторная работа №1 «Исследование термоэлектрического эффекта»
Физические основы теории термопар
В основу способа измерения температур с помощью термопар положены термоэлектрические явления, открытые Зеебеком в 1821 г. Применение этих явлений к измерению температур основано на существовании определенной зависимости между термоэлектродвижущей силой (термо-ЭДС), устанавливающейся в цепи, составленной из однородных проводников, и температурами мест их соединения. Если взять цепь (рисунок 1.1), составленную из двух разнородных проводников А и В (например, меди и платины), то при подогреве спая 1 в цепи появляется электрический ток, который в более нагретом спае 1 направлен от платины В к меди А, а в холодном спае 2 – от меди к платине. При подогреве спая 2 ток получает обратное направление. Такие токи называют термоэлектрическими токами, а дающие их приборы – термопарами и термобатареями. Электродвижущие силы, обусловленные неодинаковыми потенциалами в спаях, имеющих разные температуры называются термо–ЭДС
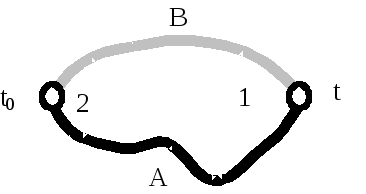
Рисунок 1.1 – Термоэлектрическая цепь из двух проводников
Для объяснения механизма возникновения термо-ЭДС воспользуемся электронной теорией, которая основывается на представление о наличии в металлах свободных электронов. В различных металлах плотность свободных электронов (число электронов в единице объёма) неодинаково и поэтому электроны, которые можно уподобить свободному газу, заполняющему межмолекулярное пространство в металле, будут находиться под неодинаковым давлением. В следствии этого в местах соприкосновения двух разнородных металлов, например, в спае 1 (рисунок 1.1), электроны будут диффундировать из металла A в металл B в большем количестве, чем обратно из металла В в металл А, и, как следствие, металл А будет заряжаться положительно, а металл В – отрицательно. Возникающее при этом в месте соприкосновения электрическое поле будет препятствовать этой диффузии, и когда скорость диффузионного перехода электронов станет равна скорости их обратного перехода под влиянием установившегося определенного поля, наступит состояние подвижного равновесия. При таком состоянии между металлами А и В возникает некоторая разность потенциалов. Так как давление электронного газа зависит также и от температуры мест соединения проводников, то ЭДС, возникающие в спаях 1 и 2 будут различны.
Кроме того, термоэлектрический ток возникает и в замкнутом однородном проводнике, если он неравномерно нагрет, так как в каждом однородном проводнике, концы которого имеют разные температуры, появляется разность потенциалов.
Учитывая оба фактора, определяющих термо-э.д.с ЕАВ (t, t0) в цепи, показанной на рисунке 1.1, можно написать:
![]() (1.1)
(1.1)
В уравнении (1.1) приняты следующие обозначения: через е обозначены результирующие ЭДС, определяемые суммарным эффектом, т.е. ЭДС, возникающими в местах соприкосновения проводников, и ЭДС, обусловленными разностью температур концов проводников А и В;через индексы АВ внизу символа обозначены проводники, между которыми результирующая ЭДС имеет место, причем порядок написания индексов указывает, при переходе от которого проводника к другому учитывается эта ЭДС Очевидно, что при перемене порядка индексов необходимо перед символом е изменить знак.
На основании этого, уравнение (1.1) мы можем представить в следующем виде:
![]() (1.2)
(1.2)
т.е. термо-ЭДС наблюдаемая в цепи из двух разнородных проводников, места спаев которых имеют разные температуры, равна разности результирующих ЭДС. Термо-ЭДС, которую один проводник приобретает по отношению к другому, считают положительной, если она в холодном спае направлена на от первого ко второму проводнику (например, медь по отношению к платине имеет положительную термо-ЭДС).
Из уравнения (1.2) непосредственно следует, что термо-ЭДС ЕАВ(t,t0) есть разность функций температур t и t0, но отнюдь не следует считать, что ЕАВ (t,t0) есть функция разности температур t и t0 так как для того, чтобы сделать последнее ошибочное заключение, необходимо считать линейную зависимость ЕАВ (t,t0). Для такого предположения никаких оснований нет, так как эксперимент показывает, что в действительности оно никогда не оправдывается.
Обозначая результирующую ЭДС еAB в уравнении (1.2) через f(t), мы можем написать формулу, выражающую в общем виде зависимость термо-ЭДС, возникающую в цепи из двух разнородных проводников А и В (рисунок 1.2), от температуры t и t0 мест их соединения
![]() (1.3)
(1.3)
Поддерживая температуру одного из спаев термопары (цепи) постоянной, например, полагая t0=const и вводя обозначения f(t0)=C, приходим к зависимости
![]() (1.4)
(1.4)
Если зависимость, выраженная уравнением 1.4, известна из кривой, таблицы или уравнения, составленного на основании эксперимента, т.е. путём градуировки термопары, то измерение неизвестной температуры t сводится к измерению EAB (t,t0).
При этом предполагается, что температура t0 остается неизменной, так как нарушение постоянства этой температуры влечет за собой недействительность уравнения (1.4) вследствие того, что с изменением t0 изменяется постоянная С.
Термо-ЭДС, развиваемая термопарой, невелика (0.01÷0.06 мВ на 1ºС), но все же достаточна для того, чтобы произвести ее измерение с достаточной для практических целей точностью с помощью пирометрического милливольтметра или потенциометра.
Для присоединения милливольтметра или потенциометра следует либо разорвать цепь термопары в спае 2 (рисунок 1.1), либо разорвать один из проводников (термоэлектродов).
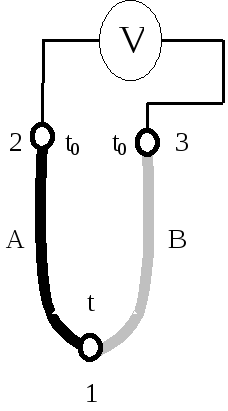
Рисунок 1.2 – Включение электроизмерительного прибора в спай термопары
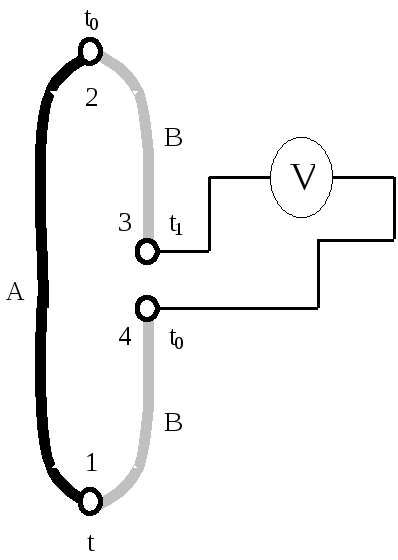
Рисунок 1.3 – Включение электроизмерительного прибора в термоэлектрод термопары
В первом случае (рисунок 1.2) у термопары будет три спая: один горячий 1 и два 2 и 3 холодные, последние должны иметь постоянную температуру t0, а во втором случае (рисунок 1.3) у термопары окажется четыре спая: один горячий 1, один холодный 2 и два нейтральных 3 и 4. Спаи 3 и 4 должны иметь одну и ту же температуру t1.
Несмотря на внешнее отличие схем (рисунки 1.2 и 1.3) от схемы (рисунок 1.1), термо-ЭДС, развиваемая термопарами, в обоих случаях будет одинакова, если одинаковы будут температуры горячих и холодных спаев, так как термо-ЭДС термопары не изменяется от введения в её цепь третьего проводника, если температуры концов этого проводника одинаковы.
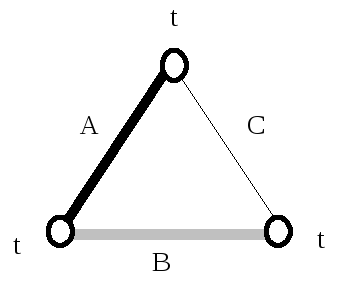
Рисунок 1.4 – Термоэлектрическая цепь из трех проводников
На основании закона Вольта (закона последовательных контактов) в замкнутой цепи, составленной из двух или любого числа разнородных проводников A, B, C,….,N в том случае, когда температуры мест их соединений одинаковы и отсутствуют посторонние ЭДС, нельзя получить тока, так как при обходе этой цепи мы опять придём к исходному проводнику и вследствие этого сумма ЭДС этой цепи будет равна нулю. Этот закон является прямым следствием второго закона термодинамики, так как, если бы сумма ЭДС в подобной цепи не равнялась нулю, то в цепи был бы ток. Если бы в цепи имелся ток, то часть цепи стала бы нагреваться, а другая – охлаждаться, что означало бы, что тепло переходит от низшей температуры к высшей без приложения внешней работы. Это противоречит второму закону термодинамики, и мы делаем вывод, что сумма ЭДС в такой цепи равна нулю.
Для случая трех разнородных проводников (рисунок 1.4), спаи которых имеют одну и ту же температуру t, будем иметь:
![]() (1.5)
(1.5)
т.е. сумма ЭДС в замкнутой цепи из разнородных металлических проводников при одной и той же температуре мест их соединения равна нулю. Из этого так же следует, что
![]() (1.6)
(1.6)
т.е. если известна ЭДС двух металлов по отношению к третьему, то этим самым определяется и ЭДС между первыми двумя.
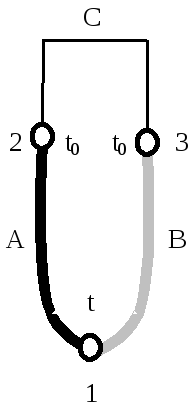
Рисунок 1.5 – Схема термопары с включенным в ее спай проводником С
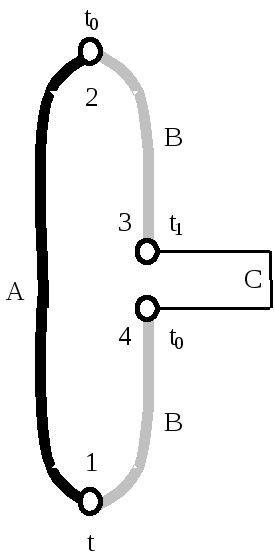
Рисунок 1.6 – Схема термопары с включенным в ее термоэлектрод проводником С
Далее рассмотрим цепь (рисунок 1.5) из трёх проводников А, В, и С, у которой температуры спаев 2 и 3 одинаковы и равны t0 определим термо-ЭДС Е для этой цепи в соответствии с принятыми условиями:
![]() (1.7)
(1.7)
Принимая во внимание уравнение (1.5), из которого вытекает, что
![]()
и подставляя это значение в уравнение (1.7), получим:
![]()
т.е. уравнение полностью совпадает с уравнением (1.2).
Рассмотрим теперь цепь, изображённую на рисунке 1.6. Полагая, что температуры спаев 3 и 4 равны между собой, будем иметь:
![]() (1.8)
(1.8)
Полученное
уравнение легко приводится к виду,
полностью совпадающему с уравнением
(1.2), если учесть, что ![]() и
и ![]() .
Таким образом, уравнение (1.8) принимает
вид:
.
Таким образом, уравнение (1.8) принимает
вид:
![]() .
.
Из этого следует, что термо-ЭДС термопары не изменяется от введения в её цепь третьего проводника, если температуры концов этого проводника одинаковы. Это положение легко распространить на цепь, составленную из любого числа проводников.
Таким образом, схемы (рисунки 1.2 и 1.3), при равенстве температур спаев 2 и 3 (рисунок 1.2) и 3 и 4 (рисунок 1.3) проводника С, термоэлектрически эквивалентны со схемой (рисунок 1.1), при этом в случае схемы (рисунок 1.3) абсолютное значение температуры t1 никакой роли не играет.
Из сказанного выше следует, что способ изготовления спая (сваркой, спайкой и т.д.) на величину термо-ЭДС не влияет, если только размеры спая таковы, что температура его во всех точках одинакова. Положение это верно, и для всех вообще токоведущих элементов термоэлектрической цепи.
Нарушение же равенства температур, концов третьего проводника, включаемого в цепь термопары, вызывает появление паразитной термо-ЭДС, которая будет зависеть от свойства проводника и от температуры мест его присоединения.
Предположим, что в схеме (рисунок 1.5) температура спая 2 проводника С с проводником А не равна температуре t0 спая 3 и имеет отличное от t0 значение t0', причем t0< t0'. В этом случае термо-ЭДСв цепи будет равна:
![]() (1.9)
(1.9)
Вычитая из уравнения (1.2) уравнение (1.9), получим:
![]() (1.10)
(1.10)
или, воспользовавшись уравнением (1.6), получим:
![]() (1.11)
(1.11)
В этом уравнении правая часть представляет собой термо-ЭДС EAC(t0',t0), развиваемую термопарой, составленной из проводника С и термоэлектрода А, концы которого имеют температуры t0' и t0.
Аналогично предыдущему предположим, что в схеме рис.1.6 температура спая 4 проводника С с проводником В не равна температуре t1 спая 3 и имеет значение t1'(t1< t1'). В этом случае термо-ЭДС будет равна:
![]() .
(1.12)
.
(1.12)
Вычитывая из уравнения (1.2) уравнение (1.12), получим:
![]() (1.13)
(1.13)
Из уравнения (1.11) и (1.13) видно, что при неравенстве температур холодных спаев (в случае схемы (рисунок 1.5)) или нейтральных (в случае схемы (рисунок 1.6)) термо-ЭДС термопары уменьшается на величину термо-ЭДС паразитной термопары, составленной из проводника С в паре с термоэлектродом А для схемы (рисунок 1.5) и с проводником В для схемы (рисунок 1.6).
Из этого следует, что в цепи пирометра нежелательно употреблять проводники, значительно различающиеся термоэлектрически, даже там, где постоянство температур относительно обеспечено. Например, для изготовления добавочных и регулировочных сопротивлений следует избегать применения константана, дающего высокую термо-ЭДС с медью, и рекомендуется применять только манганин.
Практическая часть
Задание: Исследовать зависимость ЭДС термопары от температуры при нагревании и остывании
Цель работы: исследовать термоэлектрические явления цепи, состоящей из разнородных проводников.
Приборы и оборудование: термопара градуировки ХА (хромель-алюмель), термопара градуировки ХК (хромель-копель), нагревательный элемент, лабораторный автотрансформатор (ЛАТР), вольтметр В7-21 или В7-16А, соединительные проводники, секундомер.
Порядок выполнения работы:
Подключить нагреватель к лабораторному автотрансформатору (ЛАТРу). (Провод обозначен «Нагрев термопары»)
Подключить термопару ХК или ХА к вольтметру В7-21 или В7-16А соблюдая полярность.
Включить ЛАТР в сеть 220В.

Рисунок 1.7 – Схема лабораторной установки
С помощью регулятора напряжения и вольтметра, установленных на ЛАТРе, задать напряжение нагрева UН=50В.
С интервалом в 1 мин произвести 8 измерений ЭДС термопары. Данные занести в таблицу 1.1.
Повторить пункт 5 при UН=100В и UН=150В.
Установить UН=0В и с интервалом в 1 мин выполнить 12 измерений термо-ЭДС, данные занести в таблицу 1.2.
Таблица 1.1 – Зависимость термо-ЭДС термопары при нагревании
|
UН,В |
t,мин |
Е,мВ |
|
|
|
|
Таблица 1.2 – Зависимость термо-ЭДС термопары при остывании
|
t,мин |
Е,мВ |
Т,ºС |
|
|
|
|
Используя градуировочную таблицу (ГОСТ 3044-77) (таблица встроена в стенд) определить значения температур при остывании термопары, внести эти значения в таблицу 1.2. (Поскольку градуировочная таблица содержит значения с шагом в 5°C, для определения температуры по известной ЭДС необходимо использовать линейную интерполяцию, т.е. считать, что промежуточные значения находятся по линейному закону)
Построить график зависимости термо-ЭДС термопары от времени при нагревании.
Построить график зависимости температуры термопары от времени при остывании.
Определить постоянную времени τ переходного процесса при остывании. Постоянная времени переходного процесса при остывании показывает время, за которое разность температур термопары и окружающей среды уменьшится в 2.71828 раз. Для этого представляем зависимость температуры от времени Т(t) следующим образом:
![]() ,
,
где
Т0 – температура в начале остывания;
t – время;
t0 – момент времени в начале остывания, будем считать t0=0.
Прологорифмируем это выражение с обоих сторон:
![]()
Полученное выражение продифференцируем и выразим τ:
![]() ,
,
![]() .
.
В результат приводится среднее значение.
В случае, если расчетная часть выполняется без использования среды MathCad, постоянную времени можно вычислить приближенно по двум значениям температуры: в начале и в конце остывания. Если задаться исходным уравнением и подставить в него значения для конца процесса остывания, то можно получить постоянную времени.
![]() ;
;
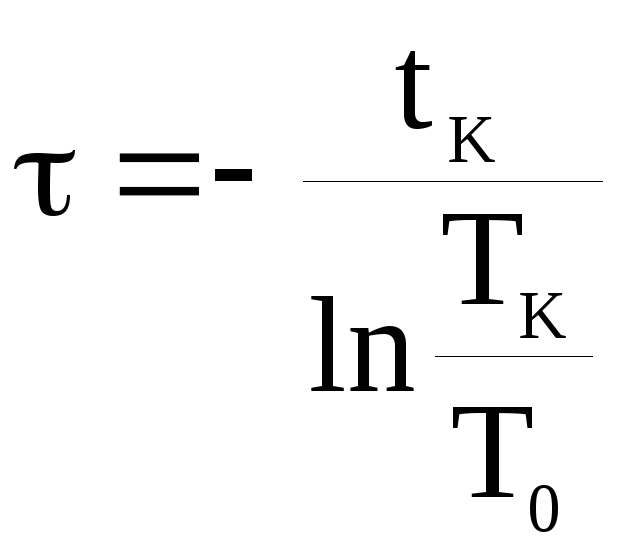 ,
,
где
ТК – температура в конце остывания;
tК – момент времени конца остывания.
Определить время запаздывания термопары tЗ=3τ.
С помощью Microsoft Word и MathSoft MathCad выполнить отчет по лабораторной работе, который должен включать:
титульный лист
теоретическую часть,
задание, цель исследования, приборы и оборудование
порядок проведения лабораторной работы, в который помещен расчет и результаты, выполненные в MathCad
выводы по работе
Отчет сдается в распечатанном виде.
