6. Баланс мощностей:

Ток J3_1 данной по условию цепи, который исключается при замене источника тока J3 эквивалентным ЭДС, найдем по первому закону Кирхгофа:

Баланс мощностей для схемы, данной по условию.

Сумма генерируемой мощности:

Сумма потребляемой мощности:

Суммы генерируемой и потребляемой мощности равны. Значит, баланс сошелся.

Рисунок 10 – Расчет мощностей в MicroCap

7. Метод эквивалентного генератора:

Найдем ток I1 методом эквивалентного генератора:

Рисунок 11 – Суть метода эквивалентного генератора

Мысленно исключим из схемы ветвь с током I1 и рассчитаем эквивалентное ЭДС E_ekv и эквивалентное сопротивление R_ekv:

Рисунок 12 – Схема, из которой исключили ветвь с током I1

Эквивалентное ЭДС равно разности потенциалов на зажимах исключенной ветви.

Но так как φ0 и φ1 больше не являются узлами, нужно обозначить оставшиеся узлы как φ1’ и φ0’ (где φ0’=0) и найти потенциалы этих точек. Затем найти потенциал точек φ0 и φ1, выразив их через потенциалы φ1 и φ0, использую закон Ома.

Для того чтобы найти φ1’, составим матричное уравнение по методу узловых потенциалов:

В новой цепи протекают новые токи:

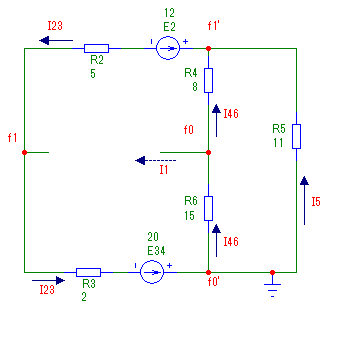
Рисунок 13 – Новые токи в цепи – I23 и I46

Найдем потенциал на зажимах ветви с током I1:

Найдем эквивалентное ЭДС:

Найдем эквивалентное сопротивление:

Рисунок 14 – Схема без ветви I1 и без источников

Сопротивления R2, R4, R5 представляют собой «звезду». Произведем замену «звезда-треугольник» и найдем сопротивления образовавшегося «треугольника»:

Рисунок 15 – После замены «звезда-треугольник»

Заменим последовательно соединенные сопротивления R24 и R45 эквивалентным сопротивлением R245, а R3 и R6 – также последовательно соединенные – сопротивлением R36.

Рисунок 16 – Схема после замены последовательно соединенных сопротивлений R24, R45, и R3, R6 соответственно эквивалентными R245 и R36

Заменим параллельно соединенные R25, R245 эквивалентным сопротивлением R2245:

Затем найдем R_ekv:

Найдем в итоге ток I1:

8. Выводы:

В данной лабораторной работе я изучил и рассчитал токи различными методами: методом контурных токов, методом узловых потенциалов, получил ток I1 методом эквивалентного генератора (активного двухполюсника). Сделал баланс мощностей для схемы с источником тока. Результаты от различных методов практически совпали, баланс мощностей сошелся.

9. Список литературы:

1. Патрушев Е.М. Методические указания по выполнению лабораторных работ по дисциплине «Общая электротехника»/ Е.М. Патрушев, Т.В. Патрушева; Алт.гос.техн.ун-т им. И. И. Ползунова. – Барнаул: Изд-во АтлГТУ, 2009. – 39с.

2. Общая электротехника – электронный учебно-методический комплекс [Электронный ресурс]. – Режим доступа: http://it.fitib.altstu.ru/neud/oe. – Загл. с экрана.