Приближенные вычисления с помощью рядов

Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.

1. Приближенное вычисление значений функций

Рассмотрим разложение функции в степенной ряд:

.

Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:

.

Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r_n(x). Для этого применяют следующие приемы:

• если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.

• если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.

• в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: (илиx<c<a).

Пример 1. Пользуясь разложением в ряд sinx, вычислить sin20^o с точностью до 0,0001.

Решение. Чтобы можно было пользоваться формулой (2), необходимо выразить значение аргумента в радианной мере. Получаем . Подставляя это значение в формулу, получаем

Полученный ряд является знакочередующимся и удовлетворяет условиям Лейбница. Так как , то этот и все последующие члены ряда можно отбросить, ограничиваясь первыми двумя членами. Таким образом,

.

Пример 2. Вычислить с точностью до 0,01.

Решение. Воспользуемся разложением , где(см. пример 5 в предыдущей теме):

Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:

.

Таким образом, мы можем отбросить этот остаток и получаем

.

Пример 3. Вычислить с точностью до 0,0001.

Решение. Воспользуемся биномиальным рядом. Так как 5³ является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5³+5.

,

так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:

, поэтому его и следующие за ним члены можно отбросить.

2. Приближенное вычисление определенных интегралов

Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подинтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.

Пример 4: Вычислить интеграл с точностью до 0,00001.

Решение. Соответствующий неопределенный интеграл не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.

Разделив почленно ряд для sinx на x , получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:

Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.

Таким образом, находим

.

Пример 5. Вычислить интеграл с точностью до 0,001.

Решение.

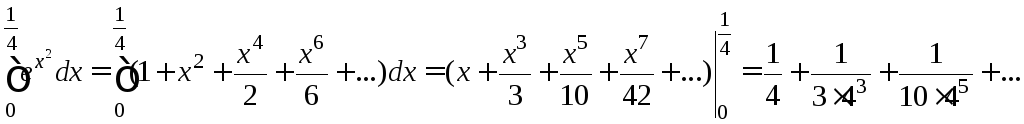
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.

.

Следовательно, .