Пример 8. Найти область сходимости степенного ряда
.
Решение.
Поскольку данный ряд не содержит четных степеней х, формулами для нахождения радиуса сходимости пользоваться нельзя. Но это степенной ряд,
поэтому
он заведомо сходится при х=2 (в центре
ряда). При любых других значениях х
исследуемый ряд можно привести к виду
,
посколькух
не зависит от n
и, следовательно, общий множитель
можно вынести за знак суммы. Сделаем
замену переменнойy=(x-2)2;
тогда
(y>0).
Этот ряд сходится при y<R,
где
.
Приy=1
имеем ряд
,
который сходится как ряд Дирихле.
Таким образом, исследуемый ряд сходится при (х-2)21, т.е. х-21, т.е. 1х3.
Областью сходимости ряда является замкнутый промежуток [1;3].
Пример
9. Найти
область сходимости ряда
.
Решение.
Сделаем замену переменной
.
Тогда задача сводится к исследованию
сходимости степенного ряда
.
Радиус сходимости найдем по формуле
Коши:
.
Приy=
имеем ряд
,
который расходится как ряд Дирихле
(р=1/2). Приy=
получаем знакочередующийся ряд
,
который сходится (по признаку Лейбница).
Таким
образом, исследуемый ряд сходится при
y
,
т.е.
,
откуда получаем условиеx>3
или x-3.
Область сходимости исследуемого ряда есть объединение двух лучей
(- -3] (3; ). Графически:
Решить: Найти промежуток сходимости функционального ряда:
A
1)
2)
3)
;
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
B
15)
16)
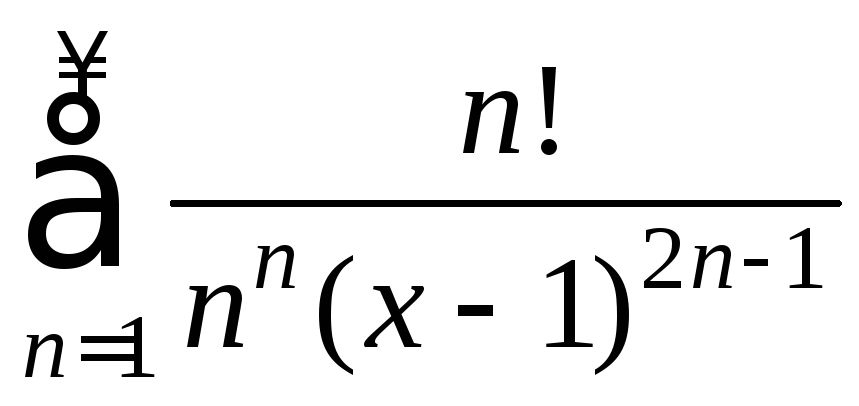
(В последних задачах при подстановке граничных точек получаются числовые ряды, для исследования которых недостаточно приведенных в данном пособии признаков, так что эту часть решения выполнять не требуется)
B Вычисление сумм степенных и числовых рядов
Внутри области сходимости степенной ряд можно почленно дифференцировать и интегрировать, т.е. если
,
то
и
.
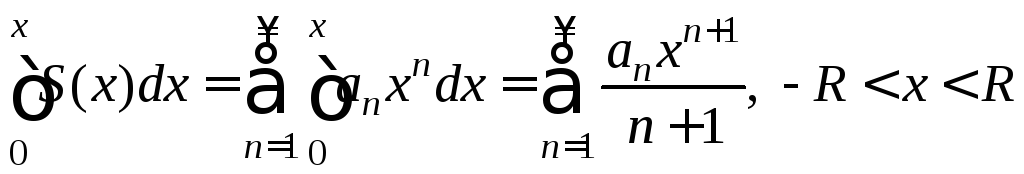Это позволяет во многих случаях вычислять сумму степенного ряда, учитывая, что сумма ряда бесконечно убывающей геометрической прогрессии вычисляется по формуле
.
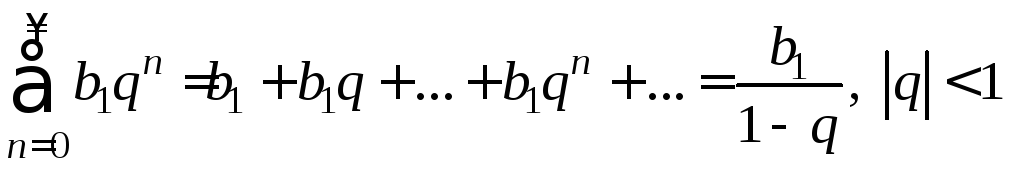Пример
1. Найти
сумму ряда
Решение:
Обозначим
.
Тогда внутри интервала сходимости
данного ряда имеем:
Полученный ряд является рядом геометрической прогрессии, причем
b1=1,
q=x.
Следовательно,
.
Далее,
.
Таким
образом,
.
Пример
2. Найти
сумму ряда
.
Решение. При дифференцировании данного степенного ряда мы не получим ряд геометрической прогрессии, т.к. не сокращается знаменатель 2n-1. Представим данный ряд в виде
и
найдем сумму ряда
:
;
.
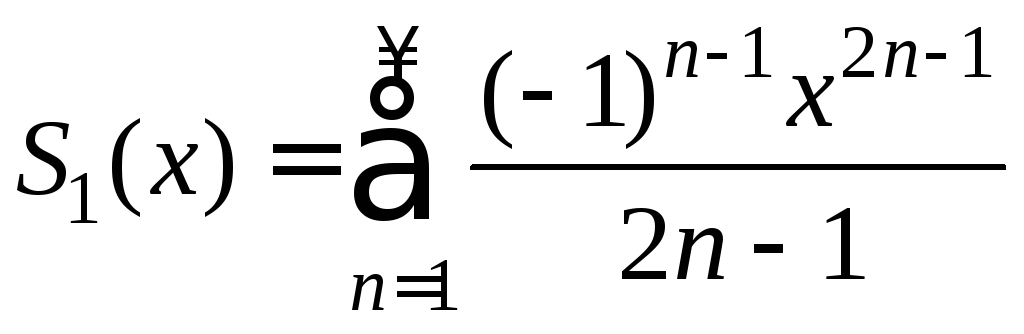Тогда
.
Пример
3. Найти
сумму ряда
Решение. Представим данный ряд в виде:
Найдем сумму ряда S1(x), предварительно проинтегрировав его:
;
.
Тогда искомая сумма ряда
.
Пример
4. Найти
сумму ряда
.
Решение.
Рассмотрим степенной ряд
.
При х=1 этот ряд принимает вид данного числового ряда, поэтому искомая сумма числового ряда есть S(1). Найдем S(x):
;
.
Таким
образом,
.
Решить: Найти сумму ряда:
1)
2)
3)
4)
5)
6)
7)
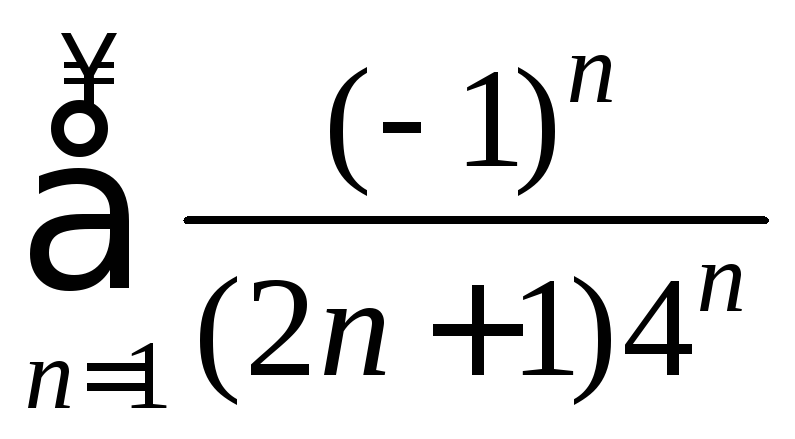8)
Разложение функций в степенные ряды
Если функция f(x)имеет на некотором интервале, содержащем точкуа, производные всех порядков, то к ней может быть применена формула Тейлора:
,
где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
,
где число
заключено между х
и а.
Если для некоторого значения х rn0 при n, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
она имеет производные всех порядков;
построенный ряд сходится в этой точке.
При а=0 получаем ряд, называемый рядом Маклорена:
Пример 1. Разложить в степенной ряд функцию f(x)=2x.
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2x, f(0) = 20=1;
f(x) = 2xln2, f(0) = 20 ln2= ln2;
f(x) = 2x ln22, f(0) = 20 ln22= ln22;
…
f(n)(x) = 2x lnn2, f(n)(0) = 20 lnn2= lnn2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:
Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -<x<+.
Пример 2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=ex.
Решение. Находим производные функции ex и их значения в точке х=-4.
f(x) = еx, f(-4) = е-4;
f(x) = еx, f(-4) = е-4;
f(x) = еx, f(-4) = е-4;
…
f(n)(x) = еx, f(n)( -4) = е-4.
Следовательно, искомый ряд Тейлора функции имеет вид:
Данное разложение также справедливо для -<x<+.
Пример 3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки х=1).
Решение. Находим производные данной функции.
…
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
С помощью признака Даламбера можно убедиться, что ряд сходится при
х-1<1. Действительно,
Ряд сходится, если х-1<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Приведем полученные подобным образом разложения в ряд Маклорена (т.е. в окрестности точки х=0) для некоторых элементарных функций:
(1)
,
(2)
,
(3)
,
(4)
,
(5)
.
(последнее разложение называют биномиальным рядом)
Пример
4. Разложить
в степенной ряд функцию
Решение. В разложении (1) заменяем х на –х2, получаем:
.
Пример
5. Разложить
в ряд Маклорена функцию
Решение.
Имеем
Пользуясь формулой (4), можем записать:
;
подставляя вместо х в формулу –х, получим:
Отсюда
находим:
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
Этот
ряд сходится в интервале
(-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Этот метод иллюстрирует теорему о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример
6. Разложить
функцию
в
ряд Тейлора в окрестности точких=3.
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):
Полученный
ряд сходится при
или –3<x-3<3,
0<x<
6 и является искомым рядом Тейлора для
данной функции.
Пример
7. Написать
ряд Тейлора по степеням (х-1)
функции
.
Решение.
Ряд
сходится при
,
или -2 <x
5.
Пример
8. Разложить
функцию
в
ряд Тейлора в окрестности точкиx=2.
Решение. Сделаем замену t=х-2:
.
Воспользовавшись
разложением (3), в котором на место х
подставим
,
получим:
Полученный
ряд сходится к заданной функции при
,
т.е. при
.
Таким образом,
Решить: Разложить заданную функцию в ряд:
A
1)
по степенямх 2)
по степенямх
3)
по степенямх 4)
по степенямх
5)
по степеням (х+1) 6)
по степеням (х-2)
7)
по степ.х 8)
в ряд Маклорена
9)
в ряд Маклорена 10)
в ряд Маклорена