
- •Тема VII. Ряды
- •Необходимый признак.
- •Достаточные признаки сходимости рядов с положительными членами.
- •Если существует конечный и отличный от нуля предел , то рассматриваемые ряды (1) и (2) сходятся или расходятся одновременно.
- •Пример 1. Доказать сходимость ряда
- •Интегральный признак Коши
- •Тогда ряд и несобственный интегралсходятся или расходятся одновременно (т.Е. Из сходимости интеграла следует сходимость ряда и наоборот).
- •Знакопеременные ряды.
- •Знакочередующийся ряд сходится, если абсолютные величины его членов убывают, а общий член стремится к нулю, т.Е. Если выполняются следующие два условия:
- •Пример 1. Исследовать сходимость степенного ряда
- •Пример 2. Найти область сходимости ряда:
- •Решение.
- •Пример 4. Найти радиус и интервал сходимости степенного ряда
- •Пример 5. Найти радиус и интервал сходимости степенного ряда . Решение
- •Пример 6. Найти промежуток сходимости ряда
- •Таким образом, на концах интервала данный ряд расходится. Промежутком сходимости является интервал .
- •Пример 7 Найти область сходимости степенного ряда
- •Пример 8. Найти область сходимости степенного ряда
- •Разложение функций в степенные ряды
- •Приближенные вычисления с помощью рядов
- •1. Приближенное вычисление значений функций
- •2. Приближенное вычисление определенных интегралов
- •3. Приближенное решение задачи Коши для обыкновенного дифференциального уравнения
- •Ряд Фурье
Интегральный признак Коши
Пусть члены ряда
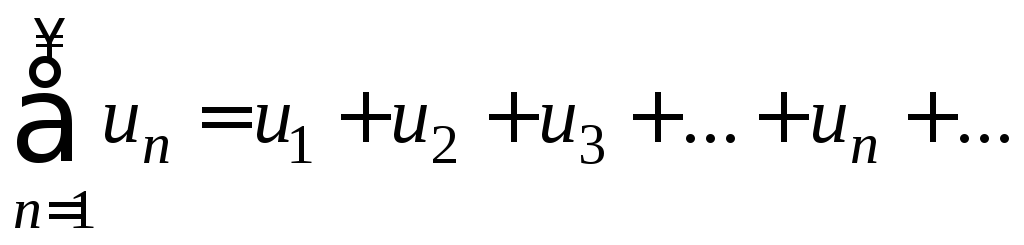 положительны
и не возрастают, т.е.
положительны
и не возрастают, т.е.
![]() и пусть f(x)
– такая непрерывная, положительная и
невозрастающая функция, что f(1)=u1,
f(2)=u2,…,f(n)=un,…
и пусть f(x)
– такая непрерывная, положительная и
невозрастающая функция, что f(1)=u1,
f(2)=u2,…,f(n)=un,…
Тогда ряд и несобственный интегралсходятся или расходятся одновременно (т.Е. Из сходимости интеграла следует сходимость ряда и наоборот).
Замечание. Нижним пределом интегрирования в интеграле может быть любое другое положительное число из области существования функции.
Пример
1. С помощью
интегрального признака Коши доказать
сходимость ряда

Решение.
Общий член данного ряда определяется
формулой
![]() (n=1,2,3,…).
Записав в этой формуле х
вместо n,
получаем функцию
(n=1,2,3,…).
Записав в этой формуле х
вместо n,
получаем функцию
![]() .
Эта функция удовлетворяет условиям
интегрального признака Коши (она
принимает положительные значения и
убывает с возрастаниемх).
.
Эта функция удовлетворяет условиям
интегрального признака Коши (она
принимает положительные значения и
убывает с возрастаниемх).
Рассмотрим несобственный интеграл
 .
.
Предел существует и конечен, значит интеграл сходится и, следовательно, сходится и данный ряд.
Пример
2. Исследовать
на сходимость ряд

Решение.
Общий член ряда определяется формулой
![]() .
(заметим, что суммирование начинается
сn=2,
а при n=1
член ряда не определен, так как в
знаменателе содержится множитель ln1=0;
однако на исследование сходимости это
не влияет). Из формулы общего члена ряда
.
(заметим, что суммирование начинается
сn=2,
а при n=1
член ряда не определен, так как в
знаменателе содержится множитель ln1=0;
однако на исследование сходимости это
не влияет). Из формулы общего члена ряда
находим
функцию
![]() .
Рассмотрим несобственный интеграл
.
Рассмотрим несобственный интеграл
 .
.
Поскольку предел бесконечен, то интеграл расходится, поэтому расходится и данный ряд.
Пример
3. С помощью
интегрального признака исследовать на
сходимость ряд:

Решение.
Функция
 прих1
положительна, непрерывна и монотонно
убывает, т.е. удовлетворяет условиям
интегрального признака Коши.
прих1
положительна, непрерывна и монотонно
убывает, т.е. удовлетворяет условиям
интегрального признака Коши.
Рассмотрим несобственный интеграл

 .
.
Поскольку
предел равен конечному числу, а именно,
![]() ,
то интеграл сходится, значит, и данный
ряд также сходится.
,
то интеграл сходится, значит, и данный
ряд также сходится.
Пример
4. Доказать
сходимость ряда

Решение.
Функция
 прих≥1
положительна, непрерывна и монотонно
убывает. Для применения интегрального
признака следует рассмотреть несобственный
интеграл
прих≥1
положительна, непрерывна и монотонно
убывает. Для применения интегрального
признака следует рассмотреть несобственный
интеграл
 .
.
Так как несобственный интеграл равен конечному числу, т.е. сходится, значит, и данный ряд сходится.
Замечание. Аналогичным образом рассматривается вопрос о сходимости ряда Дирихле с любым положительным значением р.
Решить:
Исследовать с помощью интегрального признака сходимость рядов:
A
1)
 2)
2)![]() 3)
3)
4)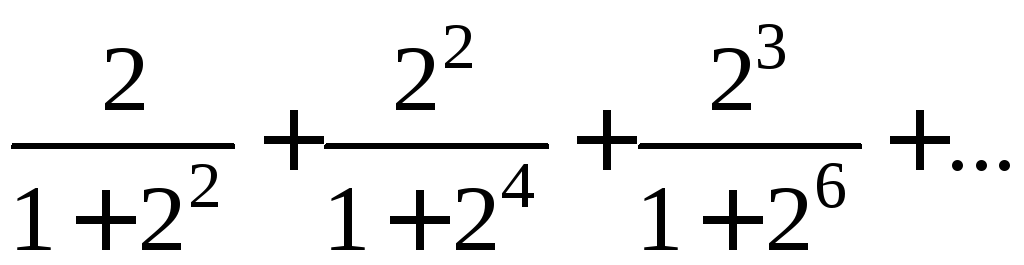 5)
5) 6)
6)
Исследовать на сходимость:
7) 8)
8)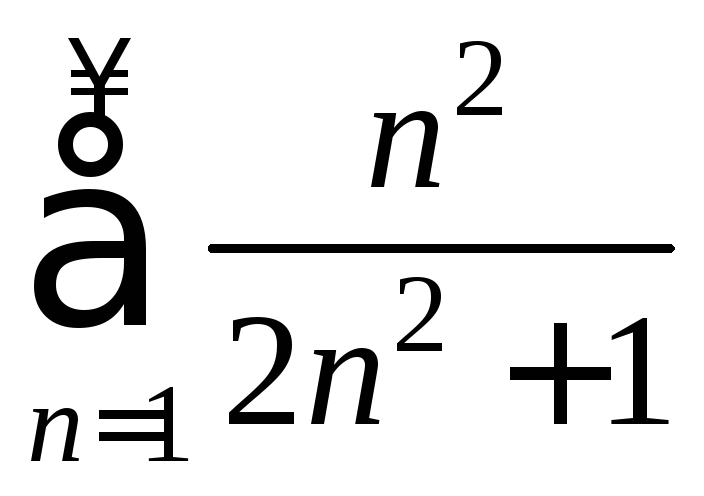 9)
9) 10)
10)
11)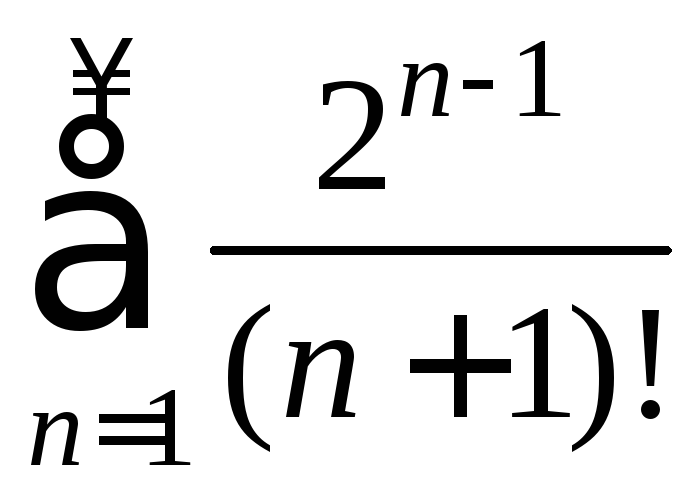 12)
12) 13)
13) 14)
14)
15)
 16)
16)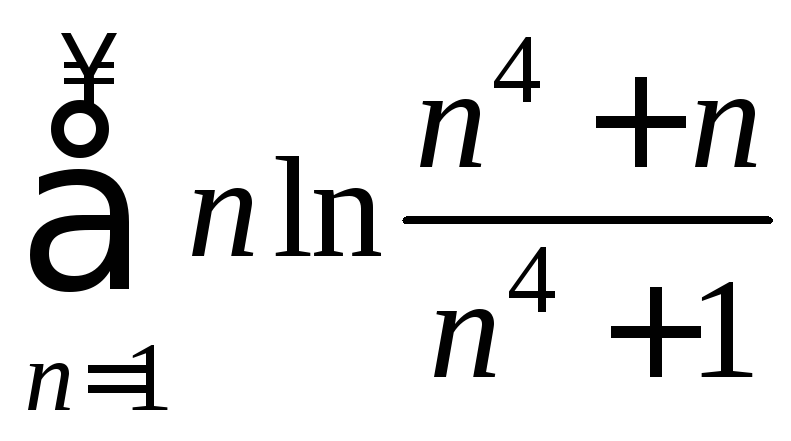 17)
17) 18)
18)
19)
 20)
20) 21)
21)
До сих пор рассматривались ряды с положительными членами. Обратимся теперь к рядам, члены которых имеют разные знаки.
Знакопеременные ряды.
Ряд, содержащий как положительные, так и отрицательные члены, называется знакопеременным.
При исследовании знакопеременного ряда
 прежде
всего составляют ряд из абсолютных
величин его членов, т.е.
прежде
всего составляют ряд из абсолютных
величин его членов, т.е.

Если
ряд
![]() сходится, то сходится и сам ряд
сходится, то сходится и сам ряд![]() .
В этом случае ряд называетсяабсолютно
сходящимся.
.
В этом случае ряд называетсяабсолютно
сходящимся.
Из
расходимости ряда
![]() не следует расходимость ряда
не следует расходимость ряда![]() .
.
Если
ряд
![]() сходится, а ряд
сходится, а ряд![]() расходится, то ряд
расходится, то ряд![]() называетсяусловно
(неабсолютно)
сходящимся.
называетсяусловно
(неабсолютно)
сходящимся.
Замечание.
Если расходимость ряда из абсолютных
величин установлена на основании
необходимого признака сходимости, т.е.
![]() ,
то и исходный знакопеременный ряд будет
расходиться, т.к. в этом случае и
,
то и исходный знакопеременный ряд будет
расходиться, т.к. в этом случае и![]() .
.
Ряд
![]() является рядом с положительными членами,
поэтому для исследования вопроса о его
сходимости можно применять ранее
рассмотренные признаки (признаки
сравнения, признаки Даламбера и Коши,
интегральный признак Коши).
является рядом с положительными членами,
поэтому для исследования вопроса о его
сходимости можно применять ранее
рассмотренные признаки (признаки
сравнения, признаки Даламбера и Коши,
интегральный признак Коши).
Пример 1.
Доказать сходимость ряда .
.
Решение.
Составим ряд из абсолютных величин членов исследуемого ряда:
 (1)
(1)
Рассмотрим ряд
вида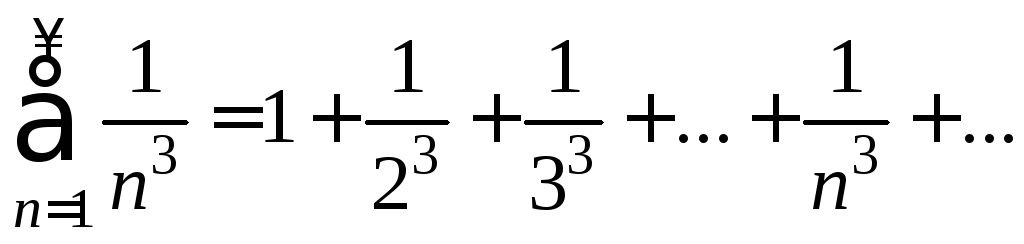 (2)
(2)
Ряд (2) является рядом Дирихле со значением р=3>1, следовательно, сходится.
К ряду (1) применим
признак сравнения:
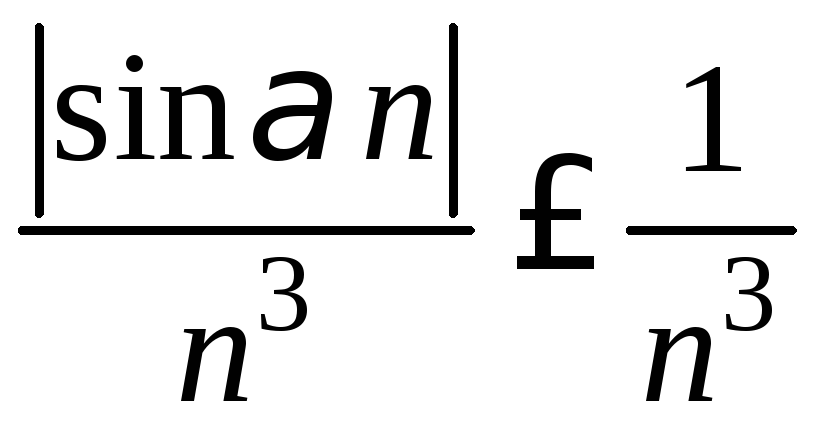 и (2) сходится(1)
сходится.
и (2) сходится(1)
сходится.
Таким образом, ряд, составленный из абсолютных величин членов заданного ряда сходится, следовательно, сам заданный ряд сходится абсолютно.
Ряд, у которого любые два соседних члена имеют разные знаки, называется знакочередующимся.
Признак Лейбница (сходимости знакочередующегося ряда)
